 Injectif surjectif
Injectif surjectif
https://dms.umontreal.ca/~broera/MAT1500Slides_190911.pdf
 1) La fonction Arccos.
1) La fonction Arccos.
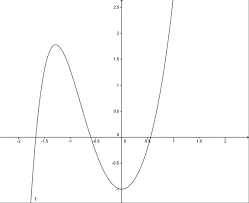
Ainsi la fonction cos n'est pas surjective
 Fonctions injectives surjectives et bijectives
Fonctions injectives surjectives et bijectives
Définition. Une fonction g est dite injective si et seulement si tout réel de l'image correspond au plus à un seul réel du domaine de définition.
 Injection surjection
Injection surjection
http://exo7.emath.fr/ficpdf/fic00003.pdf
 Fonctions : injectivité surjectivité Opérations sur les ensembles
Fonctions : injectivité surjectivité Opérations sur les ensembles
On dit que cette fonction est surjective si tout élément y ∈ F a au moins un antécédent par f. (b) La fonction exponentielle exp : R → R est injective (car
 Chapitre 4 Applications
Chapitre 4 Applications
bijective et déterminer sa fonction réciproque f−1. Exercice n◦7. Soit f l'application f :C −→ C. z ↦− → 1 + z2. 1) Montrer que f est surjective. 2) L ...
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Les fonctions f représentées ci-dessous sont surjectives : E. F f x y. E. F. Page Une fonction f est bijective si elle injective et surjective. Cela équivaut ...
 INJECTIONS SURJECTIONS
INJECTIONS SURJECTIONS
http://christophebertault.fr/documents/coursetexercices/Cours%20-%20Injections
 Applications
Applications
Exemple. La fonction x ↦→ x3 est une application surjective de R dans R. Page 15. Propriétés des applications surjectives. Proposition i) la composée de deux
 Cours - Injections surjections
Cours - Injections surjections
http://christophebertault.fr/documents/coursetexercices/Cours%20-%20Injections
 Injectif surjectif
Injectif surjectif
https://dms.umontreal.ca/~broera/MAT1500Slides_190911.pdf
 Fonctions : injectivité surjectivité Opérations sur les ensembles
Fonctions : injectivité surjectivité Opérations sur les ensembles
On dit que cette fonction est surjective si tout élément y ? F a au moins un antécédent par f. (b) La fonction exponentielle exp : R ? R est injective
 Cours : Ensembles et applications
Cours : Ensembles et applications
Supposons f bijective. Nous allons construire une application g : F ? E. Comme f est surjective alors pour chaque y ? F il existe un x ? E
 Fonctions injectives surjectives et bijectives
Fonctions injectives surjectives et bijectives
Fonctions injectives surjectives et bijectives. Injection. Définition. Une fonction g est dite injective si et seulement si tout réel de l'image correspond
 Injection surjection
Injection surjection
http://exo7.emath.fr/ficpdf/fic00003.pdf
 Chapitre 3 : Applications 1 Introduction 2 Généralités
Chapitre 3 : Applications 1 Introduction 2 Généralités
Une application injective (respectivement surjective bijective) est aussi appelée une injection (respectivement surjection
 Applications
Applications
Exemple. La fonction x ?? x3 est une application surjective de R dans R. Page 15. Propriétés des applications surjectives. Proposition i) la composée
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Autrement dit : f est surjective si et seulement si f (E) = F. Les fonctions f représentées ci-dessous sont surjectives : E. F f x y.
 IV. Applications linéaires
IV. Applications linéaires
L'application linéaire f est surjective et injective donc c'est un isomorphisme. Théor`eme. Suposons que E et F sont de dimension finie. Alors E et F sont
 Injective and surjective functions - Vanderbilt University
Injective and surjective functions - Vanderbilt University
1 Injective and surjective functions There are two types of special properties of functions which are important in many di erent mathematical theories and which you may have seen The rst property we require is the notion of an injective function De nition
 Injective and surjective functions
Injective and surjective functions
1 Functions The codomain isx >0 By looking at the graph of the functionf(x) =exwe can see thatf(x) exists for all non-negative values i e for all values ofx >0 Hence the range of the function isx >0 This means that the codomain and the range are identical and so the function is surjective
 Injective and Surjective Functions - University of Utah
Injective and Surjective Functions - University of Utah
A functionf: D!Cis calledsurjective2if for everyb2C there exists ana2Dsuch thatf(a) =b In other words associated to each possible output value there is AT LEASTone associated input value De nition 0 4 A functionf: D!Cis calledbijectiveif it is both injective and surjective
 Fonctions injectives surjectives et bijectives - uliegebe
Fonctions injectives surjectives et bijectives - uliegebe
Fonctions injectives surjectives et bijectives Injection Définition Une fonction g est dite injective si et seulement si tout réel de l’image correspond au plus à un seul réel du domaine de définition En notation mathématique on a ?1 2? ? 1 = 2 ?1=2 Remarque(s) Une fonction périodique est automatiquement non injective
 Injections Surjections and Bijections - University of Utah
Injections Surjections and Bijections - University of Utah
A function f : S !T is said to be onto or surjective if every element of T gets mapped onto More formally f is surjective if it satis es: 8t 2T;9s 2S such that f(s) = t A surjection" is a surjective function Example Suppose that S = f1;2;3;4gand T = fa;b;cg Then the map f : S !T de ned by f(1) = a f(2) = c f(3) = b f(4) = a is
 Searches related to fonction surjective PDF
Searches related to fonction surjective PDF
Nov 10 2019 · Surjective Functions Formal De?ntion: A functionf: D!Cis surjective if and only if“for all y2Cthere exists anx2Dsuch thatf(x)=y ”Casual De?nition: Every point in the co-domain has some point in the domain that maps to it Classic Example: f(x) = tanx thought of asR? 3? ?2 2 3? 5? ! R 22 2 2
What is a functionbijective if it is both injective and surjective?
Finally, we will call a functionbijective(also called a one-to-one correspondence)if it is both injective and surjective. It is not hard to show, but a crucial fact is thatfunctions have inverses (with respect to function composition) if and only if they arebijective. Example.A bijection from a nite set to itself is just a permutation.
Is f(x) x2 a surjective function?
For example, the square root of 1isn't a real number. However, like every function, this is sujective when we changeYtobe the image of the map. In this case,f(x) =x2can also be considered as a map from to the set of non-negative real numbers, and it is then a surjective function.
How do you know if a function is injective?
In general, you can tell if functions like this are one-to-one by usingthehorizontal line test; if a horizontal line ever intersects the graph in two dier-ent places, the real-valued function is not injective. In this example, it is clear that theparabola can intersect a horizontal line at more than one point.
Chapitre 3 : Applications
1 Introduction
Une fonctionf(plus précisément, une fonction réelle d"une variable réelle) est une règle qui associe à
tout réelxau plus un réel, qu"on appelle son image et qu"on notef(x). L"ensemble des réelsxdont l"image
f(x)est bien définie est l"ensemble de définition de la fonction etse noteDf.La notion d"application que nous allons étudier est une notion voisine, tellement voisine qu"on utilisera
souvent les termes " fonction" et "application" de manière interchangeable. Il y a toutefois deux différences :
a) la première est qu"une application n"est pas définie uniquement par une règle de calcul mais aussi par
un ensemble de départ et un ensemble d"arrivée. Pour toutxdans l"ensemble de départ,f(x)doit être bien
définie et appartenir à l"ensemble d"arrivée, mais il n"y a pas d"autres conditions. En particulier, l"ensemble
de départ peut-être strictement plus petit que l"ensemble de définition.La raison pour laquelle on s"intéresse aux ensembles de départ et d"arrivée est que pour une même règle
de calculx?→f(x), changer les ensembles de départ et d"arrivée peut changer les propriétés de l"application.
Nous verrons par exemple que l"application deR+dansR+qui axassociex2est croissante et bijective, alors
qu"avec la même règle de calcul, l"application deRdansRqui axassociex2n"est ni croissante ni bijective.
b) la deuxième différence est qu"une application n"associe pas forcément un réel à un réel, mais un élement
d"un ensembleFà un élément d"un ensembleE, oùEetFsont des ensembles quelconques. Par exemple,
on peut considérer l"application qui va de l"ensemble des étudiants de Dauphine dans l"ensemble des lettres
de l"alphabet, et qui a un étudiant associe la première lettre de son prénom. Autre exemple : notonsF(R,R)
l"ensemble des applications deRdansR. On peut considérer l"application qui va deF(R,R)dansR, et qui
à une applicationfassocie sa valeur en0.
Il est temps de donner des définitions précises.2 Généralités
Notations : dans tout le chapitre,E,F,GetHdésignent des ensembles.Définition.Uneapplicationfest la donnée d"unensemble de départ, d"unensemble d"arrivée, et d"unerègle
de calculqui associe à tout élémentxde l"ensemble de départ un élément de l"ensemble d"arrivée,notéf(x)
et appelé image dexparf. La règle de calcul est notéex?→f(x).Pour se donner une applicationfd"un ensemble de départEvers un ensemble d"arrivéeF, on écrit : "
soitf:E→Fune application". Supposons qu"on veuille de plus préciserla règlex?→f(x), par exemple
qu"on veuille se donner l"application deRdansRqui àxassociex2. On écrira alors : "soitf:R→R
l"application qui à tout réelxassociex2", ou encore : soit l"application f:R→R x?→x2 L"ensemble des applications deEdansFse noteF(E,F)ouFE.Egalité de deux applications.Les ensembles de départ et d"arrivée font partie de la définition d"une
application. De ce fait, siE,E?,F,F?sont des ensembles, deux applicationsf:E→Fetg:E?→F?sont
égales si et seulement si elles ont même ensemble de départ (E=E?), même ensemble d"arrivée (F=F?) et
même règle de calcul (f(x) =g(x)pour toutxdansE). Exemple 1.Soientf1,f2,f3,f4les applications suivantes : f1:R→R
x?→x2f2:R+→R x?→x2f3:R→R+ x?→x2f4:R+→R+ x?→x2 13Bien qu"elles aient en commun la règle de calculx?→x2, ces applications sont toutes différentes. Par
exemple,f1etf2sont différentes car elles n"ont pas le même ensemble de départ;f1etf3sont différentes,
car elles n"ont pas le même ensemble d"arrivée. Ces applications n"ont d"ailleurs pas les mêmes propriétés.
Par exemple,f2etf4sont croissantes, alors quef1etf3ne le sont pas.Remarques.Il faut distinguer l"ensemble de définition de la règle de calcul et l"ensemble de départ de
l"application. L"ensemble de définition de la règle de calculx?→x2estRtout entier, mais on peut très bien
prendre un ensemble de départ plus petit, comme pourf2etf4. D"autre part, il faut distinguer l"ensemble
des réels qui s"écrivent sous la formef(x)et l"ensemble d"arrivée. Il peut y avoir dans l"ensemble d"arrivée
des éléments qui ne peuvent pas s"écrire sous la formef(x), c"est à dire qui ne sont l"image d"aucun élément
de l"ensemble de départ : c"est le cas pourf1etf2, car leur ensemble d"arrivée contient des réels strictement
négatifs, et aucun réel strictement négatif ne peut s"écrire sous la formex2.Insistons : on note souventyun élément générique de l"ensemble d"arrivée. D"autre part, vous aviez l"ha-
bitude de vous donner une fonction en écrivant "soit la fonctiony=f(x)". Du coup, certains étudiants font
la confusion et ont l"impression qu"un élément de l"ensemble d"arrivée peut toujours s"écrire sous la forme
f(x). Ce n"est pas le cas.Applications bien définies: pour qu"une applicationfdeEdansFsoit bien définie, il faut que pour
tout élémentxdeE,f(x)soit bien définie et soit dansF. Tant que ces conditions sont satisfaites, on peut
très bien prendre comme ensembles de départ et d"arrivée desensemble peu naturels. Exemple.Soientf,gethles " applications " suivantes : f:R→R x?→1/xg:R?→]0,+∞[ x?→1/xh: [1,2]→[0,5] x?→x2L"applicationfest mal définie car0appartient à l"ensemble de départ, maisf(0)n"est pas défini. L"applica-
tiongest mal définie car, par exemple,-2appartient à l"ensemble de départ, mais1/(-2)n"appartient pas
à l"ensemble d"arrivée. En revanche,hest bien définie, bien que ses ensembles de départ et d"arrivée ne soient
pas particulièrement naturels. Rassurez-vous : en pratique, on ne fera pas exprès de prendre des ensembles
de départ et d"arrivée bizarres, on ne le fera que quand ce sera utile. Graphe: Soitf:E→Fune application. Le graphe defest l"ensemble des couples(x,f(x)), c"est une partie deE×F. QuandEetFsont des parties deR, on peut "dessiner" le graphe de l"application comme vous le faisiez en terminale. Abusivement, on appelle aussi"graphe" le dessin du graphe. Composition: soientE,F,F?etGdes ensembles. Soientf:E→Fetg:F?→Gdes applications.SiF=F?, ou plus généralement, siF?F?, on peut définir la composée defetg, notéeg◦f("grondf
"). C"est l"application deEdansGtelle queg◦f(x) =g(f(x))pour toutxdansE.Exemple.Soient
f: ]2,+∞[→R x?→x2+ 1etg:R\{5} →R x?→1 x-5Pour toutxdans]2,+∞[,f(x)?R\{5}. On peut donc définirg◦fet on a, pour toutxdans]2,+∞[:
g◦f(x) =1 (x2+ 1)-5=1x2-4Proposition 1Soientf:E→F,g:F→G, eth:G→Hdes applications. On ah◦(g◦f) = (h◦g)◦f
(on dit que la composition des applications est une opération associative).Preuve.Les applicationsh◦(g◦f)et(h◦g)◦fsont toutes deux égales à l"application deEdansGqui à
xassocieh(g(f(x))). 14Application identité: soitEun ensemble. On noteIdEet on appelle application identité deEl"applica-
tion :IdE:E→E
x?→x Proposition 2Pour toute applicationf:E→F, on aIdF◦f=f=f◦IdE. Preuve.Ces trois applications vont deEdansF. De plus, pour toutxdansE,IdF◦f(x) =IdF(f(x)) =f(x) etf◦IdE(x) =f(IdE(x)) =f(x).3 Antécédents, image directe, image réciproque
Antécédents: soitf:E→Fune application. Soientx?Eetz?F. Sizest l"image dexparf(i.e. f(x) =z), on dit quexest un antécédent dezparf.Un élément de l"ensemble de départ a exactement une image. Enrevanche, un élément de l"ensemble
d"arrivée peut avoir0,1ou plusieurs antécédents.Exemple.Soitf1:R→Rqui àxassociex2. Le réel-1n"a pas d"antécédents parf1,0en a exactement
un (lui-même), et3en a deux :⎷3et-⎷3. Soitf2:R+→Rqui àxassociex2. Le réel3a un unique
antécédent parf2:⎷3, car-⎷3n"appartient pas à l"ensemble de départ def2.
Soitg:R→Rqui àxassocieg(x) = sinx. Les réels n"appartenant pas à l"intervalle[-1,1]n"ont pas
d"antécédents parg. Les réels appartenant à[-1,1]en ont une infinité.Remarque: dans le cas des applications deRdansR, l"image et les antécédents d"un réel se lisent facile-
ment sur le graphe.Image directe et image réciproque
Soitf:E→Fune application. SoientA?EetB?F.
L"image (directe)deAparfest la partie deFformée des images de tous les éléments deA. On la note
f(A). On a donc : f(A) ={f(x),x?A}={y?F,?x?A,y=f(x)}Par exemple, siA={a,b,c},f(A) ={f(a),f(b),f(c)}.
L"image réciproquedeBparfest l"ensemble des éléments deEdont l"image est dansB. En d"autre termes, c"est l"ensemble des antécédent des éléments deB. On la notef-1(B). On a donc f -1(B) ={x?E,f(x)?B}={x?E,?z?B,f(x) =z}Le tableau suivant donne des exemples d"images directes parles applicationsf1,...,f4de l"exemple 1. Pour
mémoire, ces applications ont toutes la règle de calculx?→x2mais diffèrent par leurs ensembles de départ
et d"arrivée. Ces derniers sont rappelés sur la première ligne du tableau. "ND" veut dire "Non défini".
R→RR+→RR→R+R+→R+
Af1(A)f2(A)f3(A)f4(A)
{2}{4}{4}{4}{4} {-2,2}{4}ND{4}ND [-1,3][0,9]ND[0,9]ND [-1,0]?[1,3][0,9]ND[0,9]NDR+R+R+R+R+
RR+NDR+ND
15La raison pour laquelle, par exemple,f2(R)n"est pas défini, est queRn"est pas inclus dans l"ensemble de
départ def2.Le tableau suivant donne des exemples d"images réciproquespour les mêmes applications. On remarquera
que l"image réciproque d"un ensemble non vide peut être vide.R→RR+→RR→R+R+→R+
Bf-11(B)f-12(B)f-13(B)f-14(B)
{-1,2}{-⎷2,⎷2}{⎷2}NDND [-1,3]?-⎷3,⎷3??0,⎷3?NDND [-1,0]?[1,3]{0} ??-⎷3,-1???1,⎷3?{0} ??1,⎷3?NDNDR+RR+RR+
R?-∅∅NDND
RRR+NDND
La raison pour laquelle, par exemple, l"image réciproque deRparf3n"est pas définie est queRn"est pas
inclus dans l"ensemble d"arrivée def3. Proposition 3Soitf:E-→Fune application. SoientAetA?des parties deE, etBetB?des parties deF. SiA?A?alorsf(A)?f(A?). SiB?B?, alorsf-1(B)?f-1(B?).Preuve.Laissée au lecteur.
Proposition 4Soitf:E-→Fune application. SoientAetA?des parties deE, etBetB?des parties deF. Alors :1)A?f-1(f(A)) 2)f(f-1(B))?B
3)f(A?A?) =f(A)?f(A?) 4)f(A∩A?)?f(A)∩f(A?)
5)f-1(B?B?) =f-1(B)?f-1(B?) 6)f-1(B∩B?) =f-1(B)∩f-1(B?)
7) En général, les réciproques du 1), du 2) et du 4) sont fausses.
Preuve.1) Soitx?A. PosonsB=f(A). On af(x)?Bdoncx?f-1(B) =f-1(f(A)).2) Soity?f(f-1(B)). PosonsA=f-1(B). On ay?f(A), donc il existex?Atel quef(x) =y.
Commex?A=f-1(B), on af(x)?B. Doncy?B. Doncf(f-1(B))?B.3) Par double inclusion. Montrons tout d"abordf(A?A?)?f(A)?f(A?). Soity?f(A?A?). Il existe
x?A?A?tel quef(x) =y. Commex?A?A?, on ax?Aoux?A?. Six?A,f(x)?f(A)doncy?f(A) doncy?f(A)?f(A?). Sinon,x?A?, et de mêmey?f(A)?f(A?). Doncf(A?A?)?f(A)?f(A?). Montrons maintenantf(A)?f(A?)?f(A?A?). On aA?A?A?doncf(A)?f(A?A?)d"après la proposition 4. De même,f(A?)?f(A?A?). Doncf(A)?f(A?)?f(A?A?), et par double inclusion on a l"égalité.4)A∩A??Adoncf(A∩A?)?f(A). De mêmef(A∩A?)?f(A?), doncf(A∩A?)?f(A)∩f(A?).
5) Soitx?E. On a :x?f-1(B?B?)ssif(x)?B?B?donc ssi (f(x)?Bouf(x)?B?), donc ssi
(x?f-1(B)oux?f-1(B?)), donc ssix?f-1(B)?f-1(B?). Doncf-1(B?B?) =f-1(B)?f-1(B?).6) Identique à la preuve du 5) en remplaçant?par∩, et "ou" par "et".
7) Pour voir que les réciproques du 1), du 2) et du 4) sont fausses, considérons l"applicationf:R→R
qui àxassociex2. PosonsA=B=R-etA?=R+. On af(A) =R+, doncf-1(f(A)) =R?=A. Donc laréciproque du 1) est fausse. On af-1(B) ={0}, doncf(f-1(B)) ={0} ?=B, donc la réciproque du 3) est
fausse. Enfin,f(A?) =R+=f(A), doncf(A)∩f(A?) =R+, maisA∩A?={0}, doncf(A∩A?) ={0} ?= f(A)∩f(A?). Donc la réciproque du 4) est fausse. 164 Applications injectives, surjectives, bijectivesDéfinition.Soitfune application.
?festinjectivesi tout élément de l"ensemble d"arrivée aau plusun antécédent parf. ?festsurjectivesi tout élément de l"ensemble d"arrivée aau moinsun antécédent. ?festbijectivesi tout élément de l"ensemble d"arrivée aun uniqueantécédent.Cette définition peut se reformuler ainsi :fest injective (respectivement surjective; bijective) si pour
toutzdansF, l"équationf(x) =za au plus une solution dansE(respectivement au moins une solution;exactement une solution). Une application injective (respectivement surjective, bijective) est aussi appelée
une injection (respectivement surjection, bijection).Exemples.Soientf1:R→R,f2:R+→R,f3:R→R+etf4:R+→R+qui àxassocientx2. L"application
f1n"est ni injective ni surjective;f2est injective mais pas surjective;f3est surjective mais pas injective;f4
est bijective. SoitEun ensemble. L"application identité deEest bijective (prouvez-le!). Proposition 5Soitf:E→Fune application. Les propriétés suivantes sont équivalentes :1)fest injective.
2) Pour tousxetx?dansE, sif(x) =f(x?)alorsx=x?.
3) Pour tousxetx?dansE, six?=x?, alorsf(x)?=f(x?).
Preuve.. Faisons une preuve cyclique. 1)?2) : Supposonsfinjective. Soientxetx?dansEtels quef(x) =f(x?). Soitz=f(x). Six?=x?,za au moins deux antécédents distincts, ce qui est impossiblecarf
est injective. Doncx=x?et 2) est vérifié.2)?3) : évident car une implication et sa contraposée sont équivalentes.
3)?1) : soitzdansF. Siza deux antécédents distinctsxetx?alorsx?=x?maisf(x) =z=f(x?), ce
qui contredit 3). Doncza au plus un antécédent, doncfest injective. Proposition 6Soitf:E→Fune application.fest surjective si et seulement sif(E) =F.Preuve.f(E)est l"ensemble des images des éléments deE. C"est donc l"ensemble des éléments deFqui
ont au moins un antécédent. Doncf(E) =Fssi tout élément deFa au moins un antécédent parf, c"est à
dire ssifest surjective. Proposition 7Soientf:E→Fetg:F→Gdes applications. On a :1) sifetgsont injectives, alorsg◦fest injective.
2) sifetgsont surjectives, alorsg◦fest surjective.
3) sig◦fest injective, alorsfest injective.
4) sig◦fest surjective, alorsgest surjective.
5) Les réciproques sont toutes fausses.
Preuve.1) Supposonsfetginjectives. Soientxetx?dansEtels queg◦f(x) =g◦f(x?). On ag(f(x)) =g(f(x?))donc par injectivité deg,f(x) =f(x?), donc par injectivité def,x=x?. L"applicationg◦fest
donc bien injective.2) Supposonsfetgsurjectives. Soitz?G. Commegest surjective, il existey?Ftel quez=g(y). De
plus, commefest surjective, il existex?Etel quey=f(x). On a doncz=g(f(x)) =g◦f(x), doncza au moins un antécédent parg◦f. Doncg◦fest bien surjective.3) Supposonsg◦finjective. Soientxetx?dansEtels quef(x) =f(x?). On a doncg(f(x)) =g(f(x?)),
donc par injectivité deg◦f,x=x?. Doncfest injective. On peut aussi faire une preuve par contraposée : si
fn"est pas injective il existex?=x?dansEtels quef(x) =f(x?). Mais alorsg(f(x)) =g(f(x?)), doncg◦f
n"est pas injective. 174) Supposonsg◦fsurjective. Soitz?G. Commeg◦fest surjective, il existexdansEtel quez=g◦f(x).
Posonsy=f(x)(c"est à dire : appelonsyl"image dexparf). On ay?Fetz=g(y), doncza au moins un antécédent parg, doncgest surjective.5) Montrons que les réciproques de 1) et 2) sont fausses : soitf:N→Nqui à tout entier natureln
associen+1. Soitg:N→Nqui à tout entier naturelnassocien-1sin?= 0et qui à0associe0. Pour tout
entier natureln, on ag◦f(n) =g(n+ 1) = (n+ 1)-1 =n(on a utilisén+ 1?= 0pour calculerg(n+ 1)).
On a doncg◦f=IdN. L"applicationg◦fest donc bijective, donc injective et surjective. Pourtantfn"est
pas surjective (car0n"a pas d"antécédents parf) etgn"est pas injective (car0a deux antécédents parg:1
et0).Montrons maintenant que les réciproques de 3) et de 4) sont fausses. Soientf=IdRetgl"application de
RdansRqui à tout réelxassocie0. L"applicationgest donc constante. Pour tout réelx,g◦f(x) =g(x) = 0.
L"applicationg◦fn"est donc pas injective, bien quefle soit. Le lecteur vérifiera que, de même, l"application
f◦gn"est pas surjective, bien quefle soit.5 Application réciproque d"une application bijective
Soitf:E→Fune application bijective, c"est à dire que chaque élément deFa exactement un antécédent
dansE. On appelle application réciproque defl"applicationg:F→Etelle que pour toutydansF,g(y) est l"unique antécédent deyparf. On la notef-1. Proposition 8Soitf:E→F. Sifest bijective, alors pour toutxdansEet toutydansF,(y=f(x))? (x=f-1(y)).Preuve.Soitx?Eety?F. Siy=f(x)alorsxest un antécédent dey. Maisf-1(y)est l"unique antécédent
deyparf, doncf-1(y) =x. Réciproquement, six=f-1(y), alorsxest l"unique antécédent deyparf; en
particulier,xest un antécédent dey, doncf(x) =y.Proposition 9Soitf:E→Fune application.
1) sifest bijective, alorsf-1◦f=IdEetf◦f-1=IdF.
2) S"il existe une applicationgdeFversEtelle queg◦f=IdEetf◦g=IdF, alorsfest bijective et
g=f-1.3) sifest bijective, alors sa réciproquef-1aussi et(f-1)-1=f.
4) Soitg:F→G. Sifetgsont bijectives, alorsg◦fest bijective et(g◦f)-1=f-1◦g-1.
Preuve.1) Supposonsfbijective. Soitx?E. Posonsy=f(x). D"après la proposition 8,f-1(y) =xdonc f -1(f(x)) =x, doncf-1◦f=IdE. Le lecteur vérifiera que, de même,f◦f-1=IdF.2) Supposonsg◦f=IdEetf◦g=IdF. On a doncg◦fetf◦gbijectives. En particulier,g◦fest injective,
doncfest injective d"après le point 3) de la proposition 7. De même,f◦gest surjective, doncfest surjective.
L"applicationfest donc bijective, donc sa réciproquef-1existe et d"après 1),f-1◦f=IdF. En composant
l"égalitéf◦g=IdFparf-1, on obtientf-1◦f◦g=f-1◦IdF=f-1, doncg=IdF◦g= (f-1◦f)◦g=f-1.
3) Supposonsfbijective. Pour mieux comprendre la façon dont nous allons utiliser le 2), posons˜f=g-1,
˜g=f-1,˜E=Fet˜F=E. On a d"après le 1),˜g◦˜f=Id˜Eet˜f◦˜g=Id˜F. D"après le 2), on a donc˜fbijective
et ˜f-1= ˜g, c"est à diref-1bijective et?f-1?-1=f4) Supposonsfetgbijectives. Leur réciproquesf-1etg-1existent donc. De plus,(g◦f)◦(f-1◦g-1) =
g◦(f◦f-1)◦g-1=g◦IdF◦g-1=g◦g-1=IdG. De même,(f-1◦g-1)◦(g◦f) =IdE, donc d"après le
2),g◦fest bijective et(g◦f)-1=f-1◦g-1.
On utilise souvent le 2) sous la forme suivante, dont la preuve est laissée au lecteur : Proposition 10Soitf:E→Fune application. Supposons qu"il existe une applicationg:F→Etelle que, pour toutxdansEet toutydansF,y=f(x)?x=g(y). Alorsfest bijective etf-1=g. 18Cohérence des notations.Soitf:E→Fune application. SoitB?F. Quefsoit bijective ou non, on notef-1(B)l"image
réciproque deBparf. D"autre part, quandfest bijective,f-1désigne son application réciproque, et on
note donc aussif-1(B)l"image directe deBpar l"application réciproque def. Il y a donc a priori un problème
car on désigne par une même notation deux objets a priori différents. La proposition suivante montre qu"il
n"en est rien, car quandfest bijective, l"image réciproque deBparfcoincide avec l"image deBpar la réciproque def. Il n"est donc pas gênant de les noter de la même façon. Proposition 11Soientf:E→Fetg:F→Edes applications. SoitB?F. SoientA={x?E,f(x)? B}etA?={g(y),y?B}. L"ensembleAest l"image réciproque deBparf, etA?est l"image (directe) deB parg. On a : sifest bijective etgest sa réciproque, alorsA=A?. Preuve.Supposons quefsoit bijective et quegsoit sa réciproque. Montrons queA=A?par double inclusion. Six?A, alorsf(x)?B, doncg(f(x))?g(B) =A?, maisg(f(x)) =x, doncx?A?, doncA?A?. Réciproquement, six?A?, alors il existey?Btel quex=g(y). On af(x) =f(g(y)) =y, doncf(x)?B, doncx?A, doncA??Aet par double inclusionA=A?.Attention: sifn"est pas bijective, son application réciproque n"existe pas. La notationf-1(B)ne désigne
alors pas l"image deBpar l"applicationf-1(puisque cette application n"existe pas!), mais uniquement l"image
réciproque deBparf. En particulier, ce n"est pas parce que la notationf-1(B)apparaît dans un énoncé
qu"on a supposé quefétait bijective.6 Prolongements et restrictions
Définition.Soitf:E→Fune application. SoitA?EetB?Ftel quef(A)?B. On appelle restrictiondefàAcomme ensemble de départ etBcomme ensemble d"arrivée, et on notef|A→B, l"application deA
dansBqui à toutxdansAassocief(x). Cette application a la même règle de calcul quef, seuls changent
les ensembles de départ et d"arrivée.Notation : quand on restreint uniquement l"ensemble de départ (B=F: cas courant), on utilise aussi la
notationf|Apourf|A→F.Définition.Soientfetgdes applications. On dit quefest un prolongement degsigest une restriction def.
Exemples.
1) Soitf:R→Rqui àxassociex2. Soitg=f|R+→R+, c"est à dire soitg:R+→R+qui àxassociex2.
L"applicationgest une restriction def. Elle a l"avantage d"être croissante et bijective, alors quefne l"est
pas.2) Soitg:R?→Rqui àxassocie(sinx)/x. Soitf:R→Rqui àxassocie(sinx)/xsix?= 0, et qui
à0associe1. L"applicationfest un prolongement deg(on ag=f|R?). De plus, on peut montrer quefest continue surR. On dit quefest le prolongement par continuité deg. L"avantage de considérerfplutôt
quegest qu"on peut appliquer àfles théorèmes sur les fonctions continues surRtout entier (par exemple,
avecfon peut utiliser le thèorème des valeurs intermédiaires surun intervalle contenant0, alors qu"on ne
pourrait pas avecg). La proposition suivante est évidente quand on voit ce qu"elle signifie sur des "patates" :Proposition 12Soitf:E→Fune application.
quotesdbs_dbs26.pdfusesText_32[PDF] pny duo link pour iphone
[PDF] h.264 dvr android application
[PDF] duo link mode d'emploi
[PDF] i usb storer user manual
[PDF] clé usb pny non reconnue
[PDF] gmobi istick
[PDF] ud-wl01
[PDF] cours algebre application linéaire
[PDF] application bijective exercices corrigés
[PDF] rapport de stage application mobile
[PDF] rapport projet android pdf
[PDF] rapport de stage developpement application android
[PDF] conception d'une application mobile pdf
[PDF] rapport projet application android
