 resumes-de-cours-physique-et-chimie-2eme-bac-2.pdf
resumes-de-cours-physique-et-chimie-2eme-bac-2.pdf
Le système international (SI) est constitué de sept (7) grandeurs de base et de sept (7) unités de base (ou unités fondamentales du SI). Dimension. Symbole.
 Aperçu du cours du Programme du diplôme du Baccalauréat
Aperçu du cours du Programme du diplôme du Baccalauréat
International Baccalaureate®
 Bachillerato Internacional® du cours de TdC ;. • de développer la capacité de réfléchir de façon ...
Bachillerato Internacional® du cours de TdC ;. • de développer la capacité de réfléchir de façon ...
 Cours svt 1 bac international maroc pdf
Cours svt 1 bac international maroc pdf
Cours svt 1 bac international maroc pdf. Résumé cours svt 1 bac international maroc pdf. Toutes les matières du programme Les dernières annales corrigées et
 1re rentrée pour lINSA Euro-Méditerranée
1re rentrée pour lINSA Euro-Méditerranée
16 sept. 2015 ... (bac marocain sciences mathématiques sciences physiques
 BTS Commerce International
BTS Commerce International
BTS Commerce International. Le BTS CI axe ses cours sur l'international. En effet au cours de cette formation Bac + 2
 ÉTUDIANTS INTERNATIONAUX 2023
ÉTUDIANTS INTERNATIONAUX 2023
Classe préparatoire au Grandes Ecoles (CPGE) : cf. section II p. 6. ▫ Etudes Supérieures de niveau Bac+2 ou plus (validé ou en cours de validation) : cf.
 ESSEC Global BBA - PARCOURS INNOVATION & MANAGEMENT
ESSEC Global BBA - PARCOURS INNOVATION & MANAGEMENT
À la fin de leur cursus les étudiants obtiennent une licence BAC +3 reconnue et visé par le - Cours d'ouverture : géopolitique focus Afrique
 ESSEC GLOBAL BBA
ESSEC GLOBAL BBA
France (Cergy). Singapour
 Untitled
Untitled
7 écoles partenaires et 1 INSA international au Maroc. DEUX PÔLES D INSA en intégrant la filière internationale après le baccalauréat l'un des. 7 Masters ...
 Le français dans les filières scientifiques du BIOF : langue
Le français dans les filières scientifiques du BIOF : langue
2 déc. 2015 Résumé : la mise en place en 2013 des Sections Internationales du Baccalauréat Marocain apporte un changement dans la politique linguistique ...
 Cours Macro-économie Pr M.ABDELLAOUI
Cours Macro-économie Pr M.ABDELLAOUI
PIB réel mesure le revenu global de tous les agents d'une économie (compte tenu du niveau des prix). ? le taux d'inflation mesure la vitesse à laquelle les
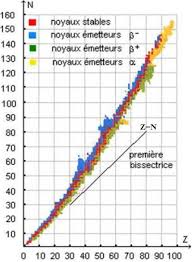
 Cours de Physique Nucléaire
Cours de Physique Nucléaire
Si compare les énergies en jeu au sein des atomes et des noyaux d'atomes on observe que l'énergie de liaison des électrons au noyau est environ un million de
 mAroc coNditioNs dAdmissioN
mAroc coNditioNs dAdmissioN
1 Avec l'obtention du BIOF (Bac international option français)
 PARTIE III : LES ECHANGES EXTERIEURS 2- Louverture de l
PARTIE III : LES ECHANGES EXTERIEURS 2- Louverture de l
2ème Bac Sciences Economiques 2011/2012 Le commerce international de marchandises a connu depuis la fin de 2ème guerre mondiale a connu une expansion ...
 Réviser son bac
Réviser son bac
chapitre 13 – Le phénotype immunitaire au cours de la vie données de la liste rouge de l'Union internationale pour la conservation de la nature (UICN) ...
 Cours Techniques du commerce international
Cours Techniques du commerce international
international. Cours niveau Bac + 2 à Bac + 5 La place de la France dans le commerce international : forces faiblesses
 Cours darithmétique
Cours darithmétique
Les notions et les théor`emes introduits ici sont généralement tout `a fait suffisants pour traiter les exercices proposées aux olympiades internationales de
 Untitled
Untitled
programme. Cadres de référence de l'examen unifié du baccalauréat - Options internationales du baccalauréat marocain - option français - 2015. Cadre de
 Cours GRH
Cours GRH
est un sous-système du système organisation : elle doit donc avoir des objectifs cohérents avec ceux du système global. Enfin la G.R.H. est influencée par
Cours d"arithm´etique
Premi`ere partie
PierreBornsztein
XavierCaruso
PierreNolin
MehdiTibouchi
D´ecembre 2004
Ce document est la premi`ere partie d"un cours d"arithm´etique ´ecrit pour les ´el`eves pr´e-
parant les olympiades internationales de math´ematiques. Le plan complet de ce cours est :1. Premiers concepts
2. Division euclidienne et cons´equences
3. Congruences
4.´Equations diophantiennes
5. Structure deZ/nZ
6. Sommes de carr´es
7. Polynˆomes `a coefficients entiers
8. Fractions continues
Cette premi`ere partie traite les quatre premiers chapitres. Les quatre derniers chapitres forment quant `a eux la deuxi`eme partie de ce cours. Contrairement `a la seconde partie, cette premi`ere partie se veut le plus ´el´ementairepossible. Les notions abstraites, souvent plus difficiles `a assimiler, mais qui clarifient les id´ees
lorsqu"elles sont comprises, ne sont ´evoqu´ees que dans la seconde partie. Nous conseillons au lecteur de bien maˆıtriser ce premier tome avant de passer `a la lecture du second.Les notions et les th´eor`emes introduits ici sont g´en´eralement tout `a fait suffisants pour
traiter les exercices propos´ees aux olympiades internationales de math´ematiques.Vous trouverez `a la fin de chaque chapitre une s´erie d"exercices de difficult´e variable mais
indiqu´ee par des ´etoiles1. Toutes les solutions sont rassembl´ees `a la fin du document.
Nous vous souhaitons bon apprentissage et bonne lecture. 1 Plus nous avons jug´e l"exercice difficile, plus le nombre d"´etoiles est important. 1Liste des abbr´evations :
AMM American Mathematical Monthly
APMO The Asian Pacific Mathematics Olympiad
CG Concours g´en´eral
OIM Olympiades Internationales de Math´ematiquesSL Short List
TDV Tournoi Des Villes
Liste des notations :
?ensemble videNensemble des entiers naturels (positifs ou nuls)
N ?ensemble des entiers naturels strictement positifsZensemble des entiers relatifs
Qensemble des nombres rationnels
Rensemble des nombres r´eelsPsymbˆole de sommation2Qsymbˆole de produit3 a|b adiviseb [x]partie enti`ere dex {x}partie d´ecimale dex pgcdplus grand commun diviseur a?bpgcd(a,b) ppcmplus petit commun multiple a?bppcm(a,b) a≡b(modN)aest congru `abmoduloN pun nombre premier v p(n)valuationp-adique den d(n)nombre de diviseurs positifs denσ(n)somme des diviseurs positifs den
?fonction indicatrice d"Euler s b(n)somme des chiffres denen baseb π(n)nombre de nombres premiers inf´erieurs ou ´egaux `an a n...a0b´ecriture en baseb n!factorielle den:n! = 1×2× ··· ×n C k ncoefficient binomial : Ck n=n! k!(n-k)! u n≂vnles suites(un)et(vn)sont ´equivalentes 2 Une somme index´ee par l"ensemble vide est ´egale `a0.3Un produit index´e par l"ensemble vide est ´egale `a1.
2Table des mati`eres
1 Premiers concepts 4
1.1 Divisibilit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2 Nombres premiers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.3 Valuationp-adique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.4 Quelques fonctions arithm´etiques . . . . . . . . . . . . . . . . . . . . . . . . 14
1.5 Nombres rationnels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2 Division euclidienne et cons´equences 24
2.1 Division euclidienne et d´ecomposition en baseb. . . . . . . . . . . . . . . . 24
2.2 Algorithme d"Euclide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.3 Algorithme d"Euclide ´etendu et th´eor`eme de B´ezout . . . . . . . . . . . . . . 28
2.4 Lemme de Gauss et cons´equences . . . . . . . . . . . . . . . . . . . . . . . . 29
2.5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3 Congruences 37
3.1 D´efinition, premi`eres propri´et´es . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.2 Crit`eres de divisibilit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.3 Ordre d"un ´el´ement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.4 Th´eor`eme chinois . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.5 Congruences modulop. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.6 Congruences modulopn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
3.7 Coefficients binomiaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
3.8 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4´Equations diophantiennes 56
4.1 Quelques r´eflexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.2 Utilisation des congruences . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.3 Descente infinie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
4.4´Equations de degr´e2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
4.5´Equations de degr´e3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
5 Corrig´e des exercices 75
5.1 Exercices de"Premiers concepts». . . . . . . . . . . . . . . . . . . . . . . 75
5.2 Exercices de"Division euclidienne et cons´equences». . . . . . . . . . . . . 103
5.3 Exercices de"Congruences». . . . . . . . . . . . . . . . . . . . . . . . . . 118
5.4 Exercices de"´Equations diophantiennes». . . . . . . . . . . . . . . . . . . 143
31 Premiers concepts
Cette section, comme son nom l"indique, pr´esente le concept de base de l"arithm´etique,`a savoir la divisibilit´e. On introduit ensuite les nombres premiers ce qui permet d"´enoncer le
th´eor`eme fondamental de l"arithm´etique (c"est-`a-dire la d´ecomposition en facteurs premiers)
dans lequel les nombres premiers jouent le rˆole de briques ´el´ementaires pour la fabrication
des nombres.1.1 Divisibilit´e
D´efinition 1.1.1Siaetbsont deux entiers, on dit queadiviseb, ou quebestdivisible para, s"il existe un entierqtel queb=aq. On dit encore queaest undiviseurdeb, ou que best unmultipledea. On le notea|b.Propri´et´es
+Siaetbsont deux entiers avecb?= 0,bdiviseasi et seulement si la fractiona b est un entier. +Tous les entiers divisent0, et sont divisibles par1. +Un entiernest toujours divisible par1,-1,net-n. +Sia|b, etb|c, alorsa|c. +Sia|b1,b2,...,bn, alorsa|b1c1+b2c2+...+bncn, quels que soient les entiersc1,c2,...,cn. +Siadivisebetb?= 0, alors|a|6|b|. +Siadivisebetbdivisea, alorsa=±b. +Siaetbsont deux entiers tels quean|bnpour un entiern>1, alorsa|b.Toutes les propri´et´es list´ees pr´ec´edemment sont imm´ediates, `a l"exception de la derni`ere dont
la d´emonstration n"est pas triviale sans bagage arithm´etique. Une preuve possible consiste`a utiliser la caract´erisation de la divisibilit´e par les valuationsp-adiques (voir paragraphe
1.3). Voyons imm´ediatement deux exercices qui montrent comment on peut manipuler la no- tion de divisibilit´e :Exercice
: Soientxetydes entiers. Montrer que2x+ 3yest divisible par7si et seulement si5x+ 4yl"est.Solution
: Supposons que7divise2x+3y, alors il divise6(2x+ 3y)-7(x+ 2y) = 5x+4y. R´eciproquement si7divise5x+ 4y, il divise6(5x+ 4y)-7(4x+ 3y) = 2x+ 3y.⎷Exercice
: Pour quels entiersnstrictement positifs, le nombren2+ 1divise-t-iln+ 1?Solution
: Sin2+1divisen+1, comme tout est positif, on doit avoirn2+16n+1, ce qui n"est v´erifi´e que pourn= 1. On v´erifie ensuite quen= 1est bien solution.⎷ 4Parties enti`eres
D´efinition 1.1.2Sixest un r´eel, on appellepartie enti`eredex, et on note[x], le plus grand entier inf´erieur ou ´egal `ax. Ainsi, on a[x]6x <[x] + 1. Remarque.On d´efinit aussi lapartie d´ecimaledex, comme la diff´erencex-[x]. La partied´ecimale dexest souvent not´ee{x}. Cette notion est moins utilis´ee que la notion de partie
enti`ere et les conventions de notations sont moins usuelles `a ce propos : lors d"un exercice,ou d"un expos´e, il est toujours de bon goˆut de commencer par pr´eciser les notations qui vont
ˆetre employ´ees par la suite.
Notons qu"il fautˆetre prudent avec les nombres n´egatifs : autant pour les nombres positifs, la partie enti`ere correspond au nombre auquel on retire ses chiffres apr`es la virgule, autantce n"est pas le cas pour les nombres n´egatifs. En effet, si on suit la d´efinition, on voit par
exemple que[-3,5] =-4.Les parties enti`eres et parties d´ecimales ob´eissent `a quelques propri´et´es ´el´ementaires que
nous listons ci-dessous :Propri´et´es ´el´ementaires
+On a toujoursx= [x] +{x}. +Pour tout r´eelx, on ax-1<[x]6x +Sixest entier,[x] =xet{x}= 0. Et r´eciproquement si l"une des deux ´egalit´es est v´erifi´ee, alorsxest entier. +[-x] =-[x]-1sauf sixest entier, auquel cas[-x] =-[x]. +Sixetysont deux r´eels,[x] + [y]6[x+y]6[x] + [y] + 1. +Sim >0est un entier, alors il y a exactement[x m ]multiples demcompris entre1et x.La d´emonstration des propri´et´es consiste en de simples manipulations de la d´efinition et
principalement de l"in´egalit´e[x]6x <[x] + 1. Elle est laiss´ee au lecteur. On remarquera que tr`es souvent les questions faisant intervenir des parties enti`eres se r´esument `a de la manipulation d"in´egalit´es comme le montre par exemple l"exercice suivant :Exercice
: On suppose que4n+ 2n"est pas le carr´e d"un nombre entier. Montrer que pour n>0, on a :h⎷ n+⎷ n+ 1i =h⎷4n+ 2i
Solution
: Remarquons tout d"abord que l"on a toujours l"in´egalit´e : n+⎷ n+ 1<⎷ 4n+ 2 En effet, en ´elevant au carr´e, on a `a comparer2n+ 1 + 2⎷ n2+net4n+ 2, soit2⎷
n 2+net2n+ 1et l"in´egalit´e devient ´evidente apr`es une nouvelle ´el´evation au carr´e.
Il reste `a prouver qu"il n"existe aucun entierktel que : n+⎷ n+ 1< k6⎷ 4n+ 2 5 soit, encore en ´elevant au carr´e qu"il n"existe aucun entierktel que :2n+ 1 + 2⎷
n2+n < k264n+ 2
Mais il est clair que4n+ 1<2n+ 1 + 2⎷
n2+net un tel entierkv´erifiraita fortiori
4n+ 1< k264n+ 2. Commekest entier, il vient forc´ementk2= 4n+ 2, mais cela n"est
pas possible puisque l"on a suppos´e que4n+ 2n"´etait pas le carr´e d"un entier.⎷ Remarque.En fait,4n+ 2n"est jamais le carr´e d"un entier. En effet, le nombre4n+ 2estpair, et s"il ´etait le carr´e d"un entier, il serait le carr´e d"un entier pair. Mais alors4n+ 2
devrait ˆetre un multiple de4, ce qui n"est, `a l"´evidence, pas le cas. L"´egalit´e pr´ec´edente de
parties enti`eres est donc valable pour tout entiern>1, sans hypoth`ese suppl´ementaire. Une propri´et´e amusante des parties enti`eres qui montre ´egalement que parfois (souvent)les manipulations d"in´egalit´es ne sont pas faciles est le th´eor`eme de Beatty que voici :
Th´eor`eme 1.1.3 (Beatty)Soientαetβdeux r´eels strictements positifs. On noteSα(resp.Sβ) l"ensemble des entiers strictement positifs qui s"´ecrivent sous la forme[nα](resp.
[nβ]) pour un certain entiern. Les ensemblesSαetSβforment une partition deN?si, et seulement siαetβsont irrationnels et v´erifient 1 +1 = 1. D´emonstration.Commen¸cons par supposer queαetβsont des irrationnels v´erifiant1 1 = 1. Soitkun entier strictement positif. Il est dans l"ensembleSαsi et seulement s"il existe un entierntel que : nα-1< k < nαl"in´egalit´e de droite ´etant stricte carαest suppos´e irrationnel. L"´equation se transforme et
donne :k ff¡ n ¡k
ff +1 ff ,k ff +1£contient un entier. De mˆeme
k?Sβsi et seulement si l"intervallei k fi ,k fi +1 h contient un entier. ff ,k ff + 1£est de longueur1et ses bornes sont irrationnelles, donc il contient un et un seul entiern. Sinet donck?Sβ. Sik´etait `a la fois ´el´ement deSαet deSβ, il y aurait un entier dans
ff ,k ff +1£et un dans l"intervallei
k fi ,k fi +1 h et donc par le mˆeme raisonnement ff ,k ff + 1£, ce qui n"est pas possible. 6 R´eciproquement, supposons queSαetSβforment une partition deN?. Consid´erons un entierkstrictement positif. Il y a£k ff y ah k fi i entiers dans{1,...,k}qui sont dansSβ. Du fait de la partition, il vient : ·k ff +·k fi =k pour toutk. En faisant tendrekvers l"infini, il vient : 1 +1 = 1 ce qui d´emontre la deuxi`eme condition. Supposons maintenant par l"absurde queαsoit rationnel. Alors il en est de mˆeme deβ d"apr`es la relation pr´ec´edente.´Ecrivonsα=a b etβ=c d . L"entieracest ´el´ement deSα(en prenantn=bc) et ´egalement ´el´ement deSβ(en prenantn=ad), ce qui est contradictoire.PgcdetPpcm
Ce paragraphe introduit les d´efinitions depgcdetppcmqui sont deux notions fonda-mentales de l"arithm´etique et en donne leurs principales propri´et´es. Les d´emonstrations qui
ne sont pas ´evidentes sont report´ees au chapitre 2 et seront vues comme cons´equence de la
division euclidienne. D´efinition 1.1.4Soientaetbdeux entiers non tous deux nuls. L"ensemble des diviseurs communs deaet debest fini et non vide, il poss`ede donc un plus grand ´el´ement appel´eplus grand commun diviseur(pgcd) deaetbet not´epgcd(a,b). Lorsquepgcd(a,b) = 1, on dit queaetbsontpremiers entre eux. De mˆemeaetbposs`edent un plus petit multiple commun positif, on l"appelle leplus petit commun multiple(ppcm) deaet debet on le noteppcm(a,b).Propri´et´es
+Sid=pgcd(a,b), alorsndiviseaetbsi et seulement sindivised. +Sim=ppcm(a,b), alorsnest un multipleaet debsi et seulement sinest un multiple dem. +Sia,betnsont des entiers non nuls etn >0, alorspgcd(na,nb) =npgcd(a,b). Si de plusndiviseaetb, alorspgcd¡a n ,b n¢=1
n pgcd(a,b). +Sid=pgcd(a,b), on peut ´ecrirea=da?etb=db?poura?etb?des nombres premiers entre eux. +Siaetbsont des entiers, l"´egalit´epgcd(a,b) =pgcd(a,a+b)est toujours v´erifi´ee lorsqu"elle a un sens. En particulier, lepgcdde deux nombres cons´ecutifs est1, et plus g´en´eralement, lepgcddeaet dea+nest un diviseur positif den. +Plus g´en´eralement, six,y,a,b,a?etb?sont des entiers alors :quotesdbs_dbs50.pdfusesText_50[PDF] cours bac pro industriel gestion
[PDF] cours bac pro melec
[PDF] cours bac pro vente
[PDF] cours bac science tunisie pdf
[PDF] cours banque assurance pdf
[PDF] cours banque pdf gratuit
[PDF] cours base de données pour debutant pdf
[PDF] cours base de données relationnelles pdf
[PDF] cours base de données site du zero pdf
[PDF] cours base de données sql pdf
[PDF] cours base de registre windows 7 pdf
[PDF] cours béton armé bael 91 pdf
[PDF] cours biblique de base
[PDF] cours biblique evangelique pdf
