Structures Algébriques 1 : Résumé de cours PDF

Résumé de cours : Structures alg`ebriques.

Résumé de cours : Structures alg`ebriques. MPSI-Maths. Mr Mamouni : myismail1@menara.ma. Source disponible sur : cсhttp://www.chez.com/myismail.

Resumé sur les structures algébriques des ensembles avec

Resumé sur les structures algébriques des ensembles avec opérations. Groupes. Groupe = ensemble G muni d'une opération ◦ : G × G −→ G notée (x

Résumé de cours sur les structures algébriques I - Notion de groupe

Résumé de cours sur les structures algébriques. I - Notion de groupe. I.1 - Généralités. Définition 1 (Notion de loi de composition interne) Soit E un ensemble

Structures algébriques.pdf

Structures algébriques. Sauf mention contraire dans le tableau ci-dessous

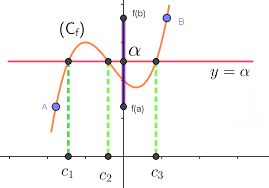Meknès Direction Provinciale : Fès Résumé Maths : 2 BAC SM BIOF

Les structures algébriques ..................... 41. Wattsapp : 06 06 39 22 82. 2. 16 avril 2020. Page 3. zouhairkarza. Prof. karza zouhair. 2 bac sm biof.

Polycopié du cours dAlgèbre 2 Structures algébriques Polynômes

En algèbre une structure algébrique est un ensemble sur lequel une opéra- La démonstration de ce dernier résultat

Structures Algébriques

Suivant les règles que vérifient ces lois de composition on dit que les ensembles correspondants portent certaines structures algébriques (groupe

Structures algébriques 1 : Résumé de cours

Pour ce qui est de la multiplication elle possède les propriétés suivantes : 1 ) C'est une loi de composition interne : ∀(a

Structures algébriques : groupes anneaux et corps

Page 1. Maths PCSI. Cours. Structures algébriques : groupes anneaux et corps. Table des mati`eres. 1 Groupes. 2. 1.1 Lois de composition interne

Structures Algébriques 1 : Résumé de cours

(1 2 3 4 5. 4 2 5 3 1. ) . La composition des applications munit Sn d'une structure de groupe : la composée de deux permutations est une permutation la

Resumé sur les structures algébriques des ensembles avec

Resumé sur les structures algébriques des ensembles avec opérations. Groupes. Groupe = ensemble G muni d'une opération ? : G × G ?? G notée (x

Résumé de cours sur les structures algébriques I - Notion de groupe

Résumé de cours sur les structures algébriques. I - Notion de groupe. I.1 - Généralités. Définition 1 (Notion de loi de composition interne) Soit E un

Résumé 16 : Structures algébriques

Résumé 16 : Structures algébriques Par récurrence on définit une structure de groupe sur un produit fini de groupes.

Résumé de cours : Structures alg`ebriques.

Résumé de cours : Structures alg`ebriques. MPSI-Maths. Mr Mamouni : myismail1@menara.ma. Source disponible sur : c?http://www.chez.com/myismail.

Structures algébriques usuelles

Structures algébriques usuelles. I. Groupes. 1. Un groupe est un couple (G ?) constitué d'un ensemble non vide G et d'une loi de composition interne ?.

Structures algébriques

Structures algébriques. Sauf mention contraire dans le tableau ci-dessous

Structures algébriques 1 : Résumé de cours

Structures algébriques 1 : Structure quotient et théorème de factorisation . ... En résumé la propriété pour H d'être distingué dans G est donc une ...

M athématiques 2 Bac SM d Excellence

15 mai 2021 Des Fiches mnémotechniques – Structures Algébriques – Résumé du cours - proposées par Badr Eddine El Fatihi – Ouarzazate 2020 - page 016.

Langages et grammaires algébriques: résumé

Langages et grammaires algébriques: résumé 1 But de l'analyse syntaxique ... L'analyseur syntaxique conna?t la structure des textes corrects ...

Structures Algébriques 1 : Résumé de cours

Université de Bordeaux

Licence de Sciences, Technologies, Santé

Mathématiques, Informatique, Sciences de la Matière et Ingénierie

Structures Algébriques 1 :

Résumé de cours

Table des matières

1 Théorie des groupes 5

1 Définition et premiers exemples . . . . . . . . . . . . . . . . . . . . . . .

2 Sous-groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2 Exemple : les sous groupes deZ. . . . . . . . . . . . . . . . . .6

3 Ordre d"un élément . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Sous-groupe engendré par une partie . . . . . . . . . . . . . . . . . . .

5 Le Théorème de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . .

5.1 Rappel : relations d"équivalence . . . . . . . . . . . . . . . . . .

5.2 Classes modulo un sous-groupe . . . . . . . . . . . . . . . . . .

2 Le groupe des permutations 13

1 Définitions et premières propriétés . . . . . . . . . . . . . . . . . . . . .

2 Cycles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Décomposition en cycles disjoints . . . . . . . . . . . . . . . . . . . . . .

4 Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Morphismes, sous-groupes normaux, groupes quotients et théorème de fac-

torisation 21

1 Morphismes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.2 Noyau, image . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Sous-groupes normaux . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Sous-groupes normaux et morphismes : le théorème de factorisation .

4 Actions de groupes 27

1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Équation des classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Une application : le théorème de Cauchy . . . . . . . . . . . . . . . . .

5 Anneaux 31

1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 L"anneau

(Z/nZ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33 3

3 Morphismes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

4 Corps finis(non traité en cours). . . . . . . . . . . . . . . . . . . . .36

6 Idéaux 39

1 Idéaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Anneaux principaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2 Exemple : les anneaux euclidiens . . . . . . . . . . . . . . . . . .

3 Arithmétique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1 PGCD, PPCM, Bézout, Gauss . . . . . . . . . . . . . . . . . . . .

3.2 Décomposition en produit d"irréductibles . . . . . . . . . . . . .

7 Polynômes et fractions rationnelles 45

1 Définitions et premières propriétés . . . . . . . . . . . . . . . . . . . . .

2 Division euclidienne . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Racines et multiplicités . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Polynômes irréductibles . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 Dérivées successives, formule de Taylor et applications(non traité

en cours). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .50

6 Fractions rationnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1 Corps des fractions d"un anneau intègre . . . . . . . . . . . . . .

6.2 Le corps des fractions rationnellesK(X). . . . . . . . . . . . . .53

Chapitre 1

Théorie des groupes

1 Définition et premiers exemplesDéfinition 1

Un groupe est la donnée d"un ensemble G et d"uneloi de composition interne GG!G (x,y)7!xy qui vérifie les propriétés suivantes :

1 )la loiest associative :8(x,y,z)2G3,x(yz) = (xy)z

2 )il existe un élément e2G, qu"on appelleélément neutre, qui est tel que :

forallx2G,xe=ex=x

3 )tout élément de G admet uninverse:8x2G,9y2Gjxy=yx=e.Proposition 1

Dans un groupe(G,):

1 )l"élément neutre est unique,

2 )tout élément x admet un unique inverse, que l"on note x1,

3 )e1=e,(x1)1=x pour tout élément x de G, et(xy)1=y1x1pour

tout couple(x,y)d"éléments de G.

Exemples:

•(Z,+) •(R,) 5 •(Z/nZ,+) •(Sn,) •(GLn(R),) racines de l"unit é. pr oduitdir ectde de uxgr oupes.

2 Sous-groupes

2.1 DéfinitionsDéfinition 2

Soit G un groupe noté multiplicativement. Une partie non vide H de G est un sous- groupe si

1 )8(x,y)2H2,xy2H

2 )8x2H,x12H.

Remarquons en particulier qu"un sous-groupe d"un groupeGcontient nécessaire- ment l"élément neutre deG. Clairement, la loi de groupe deG, quand on la restreint à un sous-groupeH, induit une structure de groupe surH. En pratique, on montrera souvent qu"un ensemble, muni d"une loi de composition interne est un groupe en l"identifiant à un sous-groupe d"un groupe connu.

La proposition suivante fournit une caractérisation très utile pour un sous-groupe :Proposition 2

Soit H une partie non vide d"un groupe G noté multiplicativement. Alors H est un sous- groupe si et seulement si

8(x,y)2H2,xy12H.

2.2 Exemple : les sous groupes deZThéorème et définition 1.1 (division euclidienne)

Pour tout couple d"entiers relatifs(a,b)avec b6=0, il existe un unique couple(q,r) d"entiers relatifs tels que( a=bq+r

0r Les entiers q et r s"appellent respectivement le quotient et le reste de la division eucli- dienne de a par b. 6
Preuve.
Existence : il y a deux cas à considérer, selon le signe dea. -sia0, on poseq0=maxfk2Ntels quekjbj ag,r=a jbjq0et q=q0ouq0selon quebest positif ou négatif. -sia<0, on poseq1=minfk2Ntels quekjbj ag,r=a+jbjq1et q=q1ouq1selon quebest négatif ou positif.
Unicité : facile.

Définition 3

1 )Le PGCD de deux entiers relatifs a et b non tous les deux nuls est l"entier d défini
par : d:=maxfk2Njk divise a et bg
2 )Le PPCM de deux entiers relatifs a et b non nuls est l"entier m défini par :
m:=minfk2Njk est un multiple commun à a et bgquotesdbs_dbs2.pdfusesText_2

[PDF] Structure construction

[PDF] structure cristalline définition

[PDF] structure cubique face centrée

[PDF] structure cubique simple

[PDF] structure cyclique des oses

[PDF] structure d une fable

[PDF] structure d une poésie

[PDF] Structure d'un atome et de son cortège électronique

[PDF] Structure d'un exposé sur les mouvements littéraires du XIX° siècle

[PDF] structure d'un exposer silvousplait

[PDF] structure dun article de presse

[PDF] structure d'un atome

[PDF] structure d'un essai

[PDF] structure d'un livre

[PDF] structure d'un manifeste

[PDF] Structures Algébriques 1 : Résumé de cours

Université de Bordeaux

Licence de Sciences, Technologies, Santé

Structures Algébriques 1 :

Résumé de cours

Table des matières

1 Théorie des groupes 5

1 Définition et premiers exemples . . . . . . . . . . . . . . . . . . . . . . .

2 Sous-groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2 Exemple : les sous groupes deZ. . . . . . . . . . . . . . . . . .6

3 Ordre d"un élément . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Sous-groupe engendré par une partie . . . . . . . . . . . . . . . . . . .

5 Le Théorème de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . .

5.1 Rappel : relations d"équivalence . . . . . . . . . . . . . . . . . .

5.2 Classes modulo un sous-groupe . . . . . . . . . . . . . . . . . .

2 Le groupe des permutations 13

1 Définitions et premières propriétés . . . . . . . . . . . . . . . . . . . . .

2 Cycles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Décomposition en cycles disjoints . . . . . . . . . . . . . . . . . . . . . .

4 Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Morphismes, sous-groupes normaux, groupes quotients et théorème de fac-

1 Morphismes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.2 Noyau, image . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Sous-groupes normaux . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Sous-groupes normaux et morphismes : le théorème de factorisation .

4 Actions de groupes 27

1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Équation des classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Une application : le théorème de Cauchy . . . . . . . . . . . . . . . . .

5 Anneaux 31

1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 L"anneau

3 Morphismes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

4 Corps finis(non traité en cours). . . . . . . . . . . . . . . . . . . . .36

6 Idéaux 39

1 Idéaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Anneaux principaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2 Exemple : les anneaux euclidiens . . . . . . . . . . . . . . . . . .

3 Arithmétique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1 PGCD, PPCM, Bézout, Gauss . . . . . . . . . . . . . . . . . . . .

3.2 Décomposition en produit d"irréductibles . . . . . . . . . . . . .

7 Polynômes et fractions rationnelles 45

1 Définitions et premières propriétés . . . . . . . . . . . . . . . . . . . . .

2 Division euclidienne . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Racines et multiplicités . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 Polynômes irréductibles . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 Dérivées successives, formule de Taylor et applications(non traité

6 Fractions rationnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1 Corps des fractions d"un anneau intègre . . . . . . . . . . . . . .

6.2 Le corps des fractions rationnellesK(X). . . . . . . . . . . . . .53

Chapitre 1

Théorie des groupes

1 Définition et premiers exemplesDéfinition 1

1 )la loiest associative :8(x,y,z)2G3,x(yz) = (xy)z

2 )il existe un élément e2G, qu"on appelleélément neutre, qui est tel que :

3 )tout élément de G admet uninverse:8x2G,9y2Gjxy=yx=e.Proposition 1

Dans un groupe(G,):

1 )l"élément neutre est unique,

2 )tout élément x admet un unique inverse, que l"on note x1,

3 )e1=e,(x1)1=x pour tout élément x de G, et(xy)1=y1x1pour

Exemples:

2 Sous-groupes

2.1 DéfinitionsDéfinition 2

1 )8(x,y)2H2,xy2H

2 )8x2H,x12H.

8(x,y)2H2,xy12H.

2.2 Exemple : les sous groupes deZThéorème et définition 1.1 (division euclidienne)

Preuve.

Unicité : facile.

Définition 3

1 )Le PGCD de deux entiers relatifs a et b non tous les deux nuls est l"entier d défini

2 )Le PPCM de deux entiers relatifs a et b non nuls est l"entier m défini par :