[PDF] FONCTION LOGARITHME NÉPÉRIEN


FONCTION LOGARITHME NÉPÉRIEN


Previous PDF Next PDF



FONCTION LOGARITHME NEPERIEN

On la note lna . La fonction logarithme népérien notée ln



FONCTION LOGARITHME NÉPÉRIEN FONCTION LOGARITHME NÉPÉRIEN

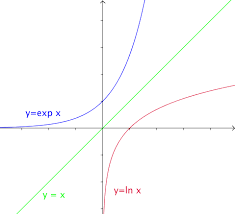
. 1. 2 exp ln. Page 4. 4. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. - Les courbes représentatives des fonctions et sont 



FONCTION LOGARITHME NEPERIEN (Partie 2) FONCTION LOGARITHME NEPERIEN (Partie 2)

Démonstration : Nous admettons que la fonction logarithme népérien est dérivable sur 0;+∞⎤⎦⎡⎣ . Posons f (x) = eln x . Alors f '(x) = (ln x)'eln x 



FONCTION LOGARITHME NÉPÉRIEN

On la note ln . ○ La fonction logarithme népérien notée



FONCTION LOGARITHME NÉPÉRIEN

Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises. L'intérêt d'établir ces tables logarithmiques est de 



FONCTION LOGARITHME NEPERIEN (Partie 1)

La fonction logarithme népérien notée ln



La fonction logarithme népérien

3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +∞[ et (ln x)′ = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...



TP 1 - Découverte de R

# logarithme népérien c(12



FONCTION LOGARITHME NEPERIEN

On la note lna . La fonction logarithme népérien notée ln



FONCTION LOGARITHME NEPERIEN

- Les courbes représentatives des fonctions exp et ln sont symétriques par rapport à la droite d'équation y = x. - Dans le domaine scientifique on utilise la.



LOGARITHME NEPERIEN

.. x ? IR+. * y = ln x. ? y ? IR e y. = x traduit le fait que les fonctions exponentielle et logarithme népérien sont réciproques l'une ...



FONCTION LOGARITHME NEPERIEN (Partie 2)

Démonstration : Nous admettons que la fonction logarithme népérien est dérivable sur 0;+????? . Posons f (x) = eln x . Alors f '(x) = (ln x)'eln x 



FONCTION LOGARITHME NÉPÉRIEN (Partie 2)

Démonstration : Pour tout réel >0 (ln ) = > 0. Page 2. 2. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 3) Convexité. Propriété : La 



FONCTION LOGARITHME NÉPÉRIEN

FONCTION LOGARITHME NÉPÉRIEN. Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg. En 1614 un mathématicien écossais



FONCTION LOGARITHME NEPERIEN (Partie 1)

La fonction logarithme népérien notée ln



La fonction logarithme népérien

3 déc. 2014 On dit que la fonction ln est la fonction réciproque de la fonction exponentielle. Remarque : Cette fonction existe bien car la fonction ...



Chapitre V : Logarithme népérien

LEÇON 05: FONCTION LOGARITHME NEPERIEN. A. SITUATION D'APPRENTISSAGE. Le médico-scolaire de ta commune organise une campagne de dépistage de la fièvre 



FONCTION LOGARITHME NÉPÉRIEN (Partie 1)

Donc : ln( × ) = ln + ln . Page 3. 3. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. Remarque : Cette formule permet de transformer un 



Terminale S - Fonction logarithme népérien

1) Définition de la fonction logarithme népérien. Soit un nombre réel strictement positif. On appelle logarithme népérien.

1

FONCTION LOGARITHME NÉPÉRIEN

- Chapitre 2/2 Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg Partie 1 : Étude de la fonction logarithme népérien

1) Continuité et dérivabilité

Vidéo https://youtu.be/3KLX-ScJmcI

Propriété : La fonction logarithme népérien est continue sur

0;+∞

Propriété : La fonction logarithme népérien est dérivable sur

0;+∞

et ln()

Démonstration au programme :

Vidéo https://youtu.be/wmysrEq4XIg

Rappel : /

En posant :

=ln(), on a : / =(ln())′

Or /

=1.

Donc : (ln())′

=1

Soit : (ln())′=

Méthode : Calculer une dérivée contenant des logarithmes

Vidéo https://youtu.be/yiQ4Z5FdFQ8

Dériver la fonction définie sur

0;+∞

par : ln() 2

Correction

ln()

Avec :

ln() =2× 1

×ln()

=1 2×

×ln()×-

ln() ×1

2ln()-

ln() ln()×(2-ln 2

2) Variations

Propriété : La fonction logarithme népérien est strictement croissante sur

0;+∞

Démonstration :

Pour tout réel >0,

ln() >0

3) Convexité

Propriété : La fonction logarithme népérien est concave sur

0;+∞

Démonstration :

Pour tout réel >0,

ln() ln() Donc la fonction logarithme népérien est concave.

4) Limites aux bornes

Propriétés : lim

ln()=-∞ et lim ln()=+∞ On dresse le tableau de variations de la fonction logarithme népérien :

0 +∞

ln() ln()

5) Tangentes en 1 et en

Rappel : Une équation de la tangente à la courbe de au point d'abscisse est de la forme :

Dans le cas de la fonction logarithme népérien, l'équation est de la forme : 1 +ln(). Au point d'abscisse 1, l'équation de la tangente est = 1 1 -1 +ln(1) soit : =-1. Au point d'abscisse , l'équation de la tangente est = 1 +ln() soit : 1 3

6) Courbe représentative

Valeurs particulières : ln(1)=0, ln()=1

Partie 2 : Croissance comparée des fonctions logarithme et puissances

Propriétés (croissances comparées) :

a) lim ln() =0 et pour tout entier naturel non nul , lim ln() =0 b) lim ln()=0 et pour tout entier naturel , lim 0 ln()=0 Démonstration du b. dans les cas où =1 (au programme) :

Vidéo https://youtu.be/LxgQBYTaRaw

En posant =ln(), on a : =

1 Or, si tend vers 0, alors =ln() tend vers -∞.

Donc : lim

ln()=lim

1→2/

1 ×=0 par croissance comparée de la fonction exponentielle et des fonctions puissances. Remarque : Les fonctions puissances imposent leur limite devant la fonction logarithme népérien. 4 Méthode : Déterminer une limite par croissance comparée

Vidéo https://youtu.be/lA3W_j4p-c8

Vidéo https://youtu.be/OYcsChr8src

)lim -ln())lim ln() -1 )lim 1 +1)ln()

Correction

a) Il s'agit d'une forme indéterminée de type "".

Levons l'indétermination :

-ln()=1- ln() E

Par croissance comparée : lim

ln() =0,

Donc : lim

1- ln() =1.

Et donc, comme limite d'un produit : lim

F1- ln()

G=+∞

Soit : lim

-ln()=+∞. b) Il s'agit d'une forme indéterminée de type "".

Levons l'indétermination :

ln() -1 #2+ 1- H lim ln =0,parcroissancecomparée. lim 1- 1 =1

Donc, comme limite d'un quotient : lim

ln() 1- 1 0 1 =0

Soit : lim

ln() -1 =0. 1 +1)ln() 1 ln()+ln() R lim ln =0,parcroissancecomparée lim ln

Donc, comme limite d'une somme : lim

ln +ln()=-∞ Et donc, comme limite d'un quotient (inverse) : lim 1 2 ln()+ln() =0 5

Soit : lim

1 2 +1)ln() =0

Partie 3 : Études de fonctions

1) Cas de fonctions contenant la fonction ⟼ln()

Méthode : Étudier les variations d'une fonction contenant des logarithmes

Vidéo https://youtu.be/iT9C0BiOK4Y

a) Déterminer les variations de la fonction définie sur

0;+∞

par =3-+2ln() b) Étudier la convexité de la fonction .

Correction

=-1+ 2

2-

Comme >0,

est du signe de 2-. La dérivée ′ est donc positive sur 0;2 et négative sur

2;+∞

On dresse le tableau de variations :

2 =3-2+2ln(2)=1+2ln(2) -1×-

2-

×1 --2+ -2 <0 On en déduit que la fonction est concave sur

0;+∞

Méthode : Étudier la position relative de la courbe de la fonction logarithme et de la droite d'équation =

Vidéo https://youtu.be/0hQnOs_hcss

Étudier la position relative de la courbe de la fonction logarithme et de la droite d'équation

0 2 +∞

+ 0 -

1+2ln(2)

6

Correction

On considère la fonction définie sur

0;+∞

par =-ln(). =1- 1 -1

Comme >0,

est du signe de -1. La dérivée ′ est donc négative sur 0;1 et positive sur

1;+∞

On dresse ainsi le tableau de variations :

1 =1-ln(1)=1

On en déduit que pour tout de

0;+∞

, on a =-ln()≥1>0 soit >ln(). La fonction logarithme est située en dessous de la droite d'équation =.

2) Cas de fonctions contenant la fonction composée ⟼ln(

Fonction Dérivée

ln()

Démonstration :

On pose :

=ln(), donc : ln() 1

Donc :

ln( , selon la dérivée d'une fonction composée. 1 Méthode : Dériver des fonctions du type ln()

Vidéo https://youtu.be/-zrhBc9xdRs

Dériver la fonction définie sur

0;2 par =ln

2-

Correction

=ln

2-

=ln(

0 1 +∞

- 0 + 1 7

Avec :

=2- =2-2

2-2

2-

Méthode : Étudier une fonction du type ln()

Vidéo https://youtu.be/s9vyHsZoV-4

Vidéo https://youtu.be/3eI4-JRKYVo

Vidéo https://youtu.be/CyOC-E7MnUw

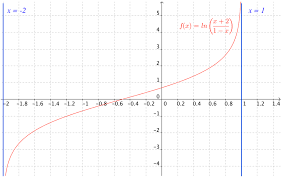
On considère la fonction définie sur

-2;1 par : =ln +2

1-

E a) Calculer les limites de aux bornes de son ensemble de définition et en déduire les

équations des asymptotes à la courbe.

b) Déterminer le sens de variations de la fonction . c) Tracer la courbe représentative de .

Correction

a) lim #→2* X lim #→2* +2=0 lim #→2*

1-=3

Donc, comme limite d'un quotient : lim

#→2* +2

1-

=0 Et donc, comme limite d'une fonction composée : lim #→2* ln +2

1-

E=-∞

En effet, si →-2, on a : =

+2

1-

→0 et donc : lim

1→-

ln()=-∞. lim R lim +2=3 lim

1-=0

,car<1

Donc, comme limite d'un quotient : lim

+2

1-

Et donc, comme limite d'une fonction composée : lim ln +2

1-

E=+∞

En effet, si →1, on a : =

+2

1-

→+∞ et donc : lim

1→./

ln()=+∞. La courbe de fonction admet deux asymptotes verticales d'équations : =-2 et =1. 8 b) =lnF +2

1-

G=ln(

), avec +2

1-

1×

1-

-(+2)×(-1)

1-

1-++2

1-

3

1-

Donc :

3 +2#

La fonction est strictement positive sur

-2;1 et 0 !1" >0.

Donc

>0. On présente le sens de variations de dans le tableau : c) -2 1quotesdbs_dbs23.pdfusesText_29
[PDF] Cours sur les fonctions logiques

[PDF] LE LOGOTYPE

[PDF] La loi normale

[PDF] Le lotissement Réglementation - Cours de Génie Civil

[PDF] Mécanismes et macro- économie monétaires

[PDF] Bien demarrer avec Flash - Site Web ? vocation éducationnel de l

[PDF] COURS DE MAINTENANCE

[PDF] La brochure 2017-2018 - Cours Municipaux d Adultes - Parisfr

[PDF] Management de l 'innovation

[PDF] Les sept principes du management de la chaîne logistique

[PDF] MRH COURS 1 Fichier - Moodle

[PDF] Management du risque

[PDF] Programme MSG CPGE ECT - cachemediaeducationgouvfr

[PDF] Management de la santé - IAE Pau-Bayonne

[PDF] Guide de Formation [COURS DE MAQUILLAGE] - Espace