 Les lois de Descartes
Les lois de Descartes
Il y a donc possibilité de réflexion totale. Page 3. Optique. %. Plus précisément si l'angle d
 III – Optique géométrique I – Lois de Descartes
III – Optique géométrique I – Lois de Descartes
III – Optique géométrique. I – Lois de Descartes. I-1) Fréquence et longueur d'onde a) Définitions. Le vide est linéaire (tout au moins dans le domaine de.
 RÉFRACTION : PRINCIPE DE FERMAT ET LOI DE SNELL
RÉFRACTION : PRINCIPE DE FERMAT ET LOI DE SNELL
Nous donnons ci-dessous des démonstrations de l'équivalence entre la loi de Descartes - Snell et le principe de Fermat dans le cas de la réfraction puis
 Fiche dexercices corrigés : Réfraction et lois de Descartes Rappel
Fiche dexercices corrigés : Réfraction et lois de Descartes Rappel
4 déc. 2012 Le plan contenant le rayon incident et la normale à la surface est le plan d'incidence. • Première loi de Descartes: Le rayon réfracté est dans ...
 Effets Doppler et Compton interférences
Effets Doppler et Compton interférences
https://hal.science/jpa-00234013/document
 Chapitre 5 - Réfraction et dispersion de la lumière
Chapitre 5 - Réfraction et dispersion de la lumière
Enoncé des deux lois de Descartes. Première loi de Descartes : Le rayon réfracté est dans le plan d'incidence. Deuxième loi de Descartes : L'angle d
 Éléments Optique Géométrique Matricielle V17.11 - Lois de Snell
Éléments Optique Géométrique Matricielle V17.11 - Lois de Snell
4 nov. 2017 Le changement de direction aux interfaces est décrit par les lois de Snell-Descartes. indice n1 indice n2. N. T. A. • u1. B. • u2 u1. A'. •. I.
 Cours doptique géométrique – femto-physique.fr
Cours doptique géométrique – femto-physique.fr
1621 L'astronome néerlandais Willebrord Snell découvre les lois de la réfraction. 1637 René Descartes démontre mathématiquement que les angles des arcs-en-ciel
 Optique géométrique et lois de Descartes
Optique géométrique et lois de Descartes
Optique géo./Lois de Descartes. OS – TD 1. Optique géométrique et lois de Descartes. I - Cadre de l'optique géométrique. 1. Rappeler les trois conséquences
 Lois de Descartes
Lois de Descartes
Lois de Descartes. Page 2. Lois de la réfraction. :normale Application à la fibre optique. Calcul de l'angle critique entre le cœur et la gaine de la.
 Cours doptique géométrique – femto-physique.fr
Cours doptique géométrique – femto-physique.fr
1621 L'astronome néerlandais Willebrord Snell découvre les lois de la réfraction. 1637 René Descartes démontre mathématiquement que les angles des arcs-en-ciel
 Exercices dOptique
Exercices dOptique
les lois de Descartes relatives `a la réfraction de la lumi`ere. b) Calculer l'angle que fait le rayon bleu avec le rayon rouge pour un.
 INTRODUCTION A LOPTIQUE GEOMETRIQUE LOIS DE
INTRODUCTION A LOPTIQUE GEOMETRIQUE LOIS DE
Chapitre 1 : Lois de Descartes et formation des images. Sonia Najid – Lycée Blaise Pascal ATS 2019-2020. 1. TD OPTIQUE 1 : INTRODUCTION A L'OPTIQUE
 III – Optique géométrique I – Lois de Descartes
III – Optique géométrique I – Lois de Descartes
III – Optique géométrique. I – Lois de Descartes. I-1) Fréquence et longueur d'onde a) Définitions. Le vide est linéaire (tout au moins dans le domaine de.
 Chapitre 2 - Lois de Snell-Descartes
Chapitre 2 - Lois de Snell-Descartes
Première loi de Snell-Descartes : les rayons réfléchi et réfracté sont dans le plan Une fibre optique sert à transporter de l'information en guidant des ...
 Chapitre 5 - Réfraction et dispersion de la lumière
Chapitre 5 - Réfraction et dispersion de la lumière
Le rayon réfracté est dans le plan d'incidence. Deuxième loi de Descartes : L'angle d'incidence i1 et l'angle de réfraction i2 vérifient la relation suivante :.
 APPROXIMATION DE LOPTIQUE GÉOMÉTRIQUE – LOIS DE
APPROXIMATION DE LOPTIQUE GÉOMÉTRIQUE – LOIS DE
Cours d'Optique (31-101). Page 1 sur 16. JN Beury. APPROXIMATION DE L'OPTIQUE. GÉOMÉTRIQUE – LOIS DE DESCARTES. I. NOTION EXPÉRIMENTALE DE RAYON LUMINEUX.
 Fiche dexercices corrigés : Réfraction et lois de Descartes Rappel
Fiche dexercices corrigés : Réfraction et lois de Descartes Rappel
4 déc. 2012 Le plan contenant le rayon incident et la normale à la surface est le plan d'incidence. • Première loi de Descartes: Le rayon réfracté est dans ...
 Chapitre 1 - OPTIQUE GEOMETRIQUE
Chapitre 1 - OPTIQUE GEOMETRIQUE
Rayons lumineux - Lois de Descartes. 1. Approximation de l'optique géométrique. On observe expérimentalement que la lumière se propage en ligne droite dans
 [PDF] Lois de Descartes
[PDF] Lois de Descartes
Lois de la réflexion 1) Les rayons incidents et réfléchis sont dans le même plan appelés plan d'incidence 2) Les angles d'incidence et de réflexion
 [PDF] Lois de Snell-Descartes - CPGE du Lycée Montesquieu
[PDF] Lois de Snell-Descartes - CPGE du Lycée Montesquieu
Première loi de Snell-Descartes : les rayons réfléchi et réfracté sont dans le plan Une fibre optique sert à transporter de l'information en guidant des
 [PDF] Les lois de Descartes
[PDF] Les lois de Descartes
Les lois de Descartes Rappels de cours I Dé nitions On dé nit le plan d'incidence comme celui généré par le rayon incident et la normale au dioptre
 [PDF] III – Optique géométrique I – Lois de Descartes
[PDF] III – Optique géométrique I – Lois de Descartes
selon les lois de Descartes : r= -i Un rayon lumineux incident étant donné on construit géométriquement la marche du rayon réfléchi correspondant en opérant
 [PDF] introduction aloptique geometrique lois de descartes et formation
[PDF] introduction aloptique geometrique lois de descartes et formation
Chapitre 1 : Lois de Descartes et formation des images Sonia Najid – Lycée Blaise Pascal ATS 2019-2020 1 TD OPTIQUE 1 : INTRODUCTION A L'OPTIQUE
 [PDF] Rayons lumineux lois de Snell-Descartes
[PDF] Rayons lumineux lois de Snell-Descartes
Optique et physique ondulatoire [Chap 5] Rayons lumineux lois de Snell-Descartes 8l dans ce cas à une distribution irrégulière et rapidement variable de
 [PDF] Lois de Snell-Descartes - ResearchGate
[PDF] Lois de Snell-Descartes - ResearchGate
4 nov 2017 · Un prisme est un élément optique utilisé pour réfracter la lumière la réfléchir ou la disper- ser en ses constituants les différents
 [PDF] Chapitre 1 Les lois de réfraction et de réflexion totalepdf
[PDF] Chapitre 1 Les lois de réfraction et de réflexion totalepdf
Partie I: Optique géométrique 1 Les lois de réfraction et de réflexion totale 2 Construction de l'image Loi Snell Descarte : Lois de Réfraction
 [PDF] Chapitre 5 - Réfraction et dispersion de la lumière - Lycée dAdultes
[PDF] Chapitre 5 - Réfraction et dispersion de la lumière - Lycée dAdultes
Première loi de Descartes : Le rayon réfracté est dans le plan d'incidence Deuxième loi de Descartes : L'angle d'incidence i1 et l'angle de réfraction i2
 LOIS DE LOPTIQUE GÉOMÉTRIQUE
LOIS DE LOPTIQUE GÉOMÉTRIQUE
Cours et exercices sur les lois de Snell-Descartes Ce premier chapitre rappelle les bases de l'optique géométrique : la notion de rayon lumineux
Quelles sont les 3 lois de Descartes ?
« Le rayon réfracté et le rayon réfléchi appartiennent au même plan que le rayon incident et la normale. » Passons à la deuxième loi de Descartes. La deuxième loi de Descartes concerne le rayon réfléchi, tandis que la 3ème loi de Descartes concerne le rayon réfracté.Quels sont les deux lois de Descartes ?
Première loi de Snell-Descartes : le rayon réfracté, le rayon incident et la normale appartiennent au même plan. Ce plan est appelé plan d'incidence. Deuxième loi de Snell-Descartes sur la réflexion : les angles d'incidence et de réflexion sont égaux : .Comment utiliser les lois de Snell-descartes ?
La loi de Snell (Snell Descartes en France) permet de calculer la direction d'un rayon lumineux incident puis réfracté par un milieu optique, si l'on connaît l'indice de réfraction des milieux traversés, et l'angle du rayon incident avec la normale (perpendiculaire) à la surface au point rencontré par le rayon.- L'optique géométrique repose sur deux lois fondamentales : Propagation rectiligne de la lumière : dans un milieu transparent, homogène et isotrope, la lumière se propage en ligne droite : les supports des rayons sont des droites.
Exercices d"Optique
" (...) que mon corps est le prisme inaperçu, mais vécu, qui réfracte le monde aperçu vers mon "Je». Ce double mouvement de conscience,à la fois centrifuge et centripète, qui me relie au monde, transforme celui-ci par là même, lui donne une détermination, une qualification nouvelle. » EdmondBarbotin-Humanité de l"hommeAubier, p. 48 (1970) ?Lois de Snell-Descartes O1? ???Ex-O1.1Mise en jambes1)Refaire le sch´ema ci-contre en ne
laissant que les rayons lumineux existant r´eellement.2)Donner toutes les relations angulaires
possibles en pr´ecisant pour chacune si elle est d"origine g´eom´etrique ou optique. ???Ex-O1.2La loi de la r´efractionUn rayon lumineux dans l"air tombe sur la
surface d"un liquide; il fait un angleα= 56◦avec le plan horizontal.
La d´eviation entre le rayon incident et le rayon r´efract´eestθ= 13,5◦. Quel est l"indicendu
liquide?R´ep. :n= 1,6.
???Ex-O1.3Constructions de Descartes et de Huygens Montrer que les deux constructions suivantes permettent de tracer le rayon r´efract´e.1) Construction de Descartes:
◦tracer les cercles de rayonsn1etn2; ◦soitMl"intersection du rayon incident avec le cercle de rayon n 1; ◦soitPl"intersection du cercle de rayonn2et de la droite orthogonale `a la surface de s´eparation passant parM; ◦le rayon r´efract´e n"est autre queOP.2) Construction de Huygens:
◦tracer les cercles de rayons 1/n1et 1/n2; ◦soitMl"intersection du rayon incident avec le cercle de rayon 1/n1; ◦tracer la tangente enMau cercle de rayon 1/n1; ◦soitIle point d"intersection de la tangente avec la surface de s´eparation; ◦soitPl"intersection du cercle de rayon 1/n2et de la se- conde tangente trac´ee; ◦le rayon r´efract´e n"est autre queOP. ???Ex-O1.4Dispersion par le verreLe tableau ci-contre donne les longueurs d"onde,
dans le vide, de deux radiations monochroma- tiques et les indices correspondants pour deux types de verre diff´erents.Couleurλ0(nm)n(crown)n(flint)
rouge656,31,5041,612 bleu486,11,5211,6711)Calculer les fr´equences de ces ondes lumineuses. D´ependent-elles de l"indice du milieu?
On prendrac0= 2,998.108m.s-1.
Exercices d"Optique2008-2009
2)Calculer les c´el´erit´es et les longueurs d"onde de la radiation rouge dans les deux verres.
3)a) Un rayon de lumi`ere blanche arrive sur un dioptre plan air-verre,
sous l"incidencei= 60◦. L"indice de l"air est pris ´egal `a 1,000. Rappeler les lois deDescartesrelatives `a la r´efraction de la lumi`ere. b) Calculer l"angle que fait le rayon bleu avec le rayon rougepour un verre crown, puis pour un verre flint. Faire une figure. c) Quel est le verre le plus dispersif? i r R rB ???Ex-O1.5Relation entre l"indice et la longueur d"ondeOn mesure l"indice d"un verre pour
diff´erentes longueurs d"onde (dans le vide) :λ(nm)400500600700800
n(λ)1,5001,4891,4821,4791,476 On veut d´eterminer les coefficientsAetBde la relation deCauchy:n(λ) =A+Bλ2.1)D´eterminer les unit´es deAet deB.
2)Expliquer pourquoi il ne faut pas ´etudiernen fonction deλ, maisnen fonction de1
λ2.
3) `A l"aide d"une calculatrice, d´eterminerAetBpar r´egression lin´eaire.4)En d´eduirenpourλ= 633nm.
???Ex-O1.6Courbure d"une fibre optique Une fibre optique est constitu´e d"une ˆame en verre d"indicen1= 1,66 et de diam`etred= 0,05mmentour´ee d"une gaine en verre d"indicen2= 1,52. On courbe la fibre ´eclair´ee sous incidence normale. Quel est est le rayon de courbureRminimal pour lequel toute la lumi`ere incidente traverse la fibre?R´ep :Il fautR >d
2.n1+n2n1-n2
???Ex-O1.7Flotteur Un disque en li`ege de rayonrflotte sur l"eau d"indicen; il soutient une tige plac´ee perpendiculairement en son centre. Quelle estla longueur hde la partie de la tige non visible pour un observateur dans l"air?Citer les ph´enom`enes mis en jeu.
R´ep. :h=r⎷
n2-1. ???Ex-O1.8Le point de vue du poisson Un poisson est pos´e sur le fond d"un lac : il regarde vers le haut et voit `a la surface de l"eau (d"indicen= 1,33) un disque lumineux de rayonr, centr´e `a sa verticale, dans lequel il aper¸coit tout ce qui est au-dessus de l"eau.1)Expliquer cette observation.
2)Le rayon du disque estr= 3,0m.`A quelle profondeur se trouve le poisson?
R´ep. :h= 2,6m.
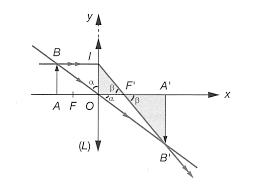
???Ex-O1.9Lame `a faces parall`elesOn consid`ere une lame `a faces parall`eles en verre (indicen) plong´ee dans l"air. Elle peut ˆetre
consid´er´ee comme l"association de deux dioptres plans parall`eles. Il y a donc stigmatisme approch´e dans les conditions deGauss(Cf. le¸con suivante).1)Faire une figure montrant qu"un rayon d"incidenceia subi `a sa sortie un simple d´eplacement
d"une distanced=e.sin(i-r) cosr(rest l"angle de r´efraction `a la premi`ere r´efraction;eest l"´epaisseur de la lame).2)Montrer que la position de l"image est telle queAA?=e(1-1
n) et que ce d´eplacement appa- rent a lieu dans le sens de la lumi`ere. CalculerAA?pour une vitre d"´epaisseur 1mm. Conclusion?2http ://pcsi-unautreregard.over-blog.com/qadripcsi@aol.com
2008-2009Exercices d"Optique
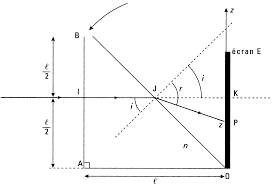
???Ex-O1.10Indice d"un liquideUne cuve en verre a la forme d"un prisme de
section droite rectangle isoc`ele. Elle est pos´ee horizontalement sur une des arˆetes de longueur ldu triangle isoc`ele, et le sommet oppos´e `a ce cˆot´e est ouvert pour permettre de remplir la cuve d"un liquide transparent d"indicen. Un pinceau de lumi`ere est envoy´e horizontale- ment sur la face verticale de la cuve, dans un plan de section droite, `a la hauteurl 2.Ce rayon ´emerge au-del`a de l"hypoth´enuse et rencontre en un pointPun ´ecranEplac´e vertica-
lement `a la distancelde la face d"entr´ee du dispositif. On n´eglige l"effet dˆu aux parois en verre
sur la propagation du pinceau de lumi`ere.1)Quelle limite sup´erieure peut-on donner `a la valeur de l"indice?
2)Quel est l"indicendu liquide contenu dans la cuve en fonction delet dez?
3)A.N. : calculernavec :l= 30cmetz= 6,7cm.
2 sin?
i+ arctan?l-2zl?? ;3)n= 1,36 (´ethanol peut-ˆetre). ???Ex-O1.11Deux prismes accol´es Deux morceaux de verre taill´es sous forme de tri- angles rectangles et isoc`eles d"indices respectifsNetn ont leur faceABcommune. Un rayon incident frappe ADsous une incidence normale, se r´efracte enI1, se r´efl´echit enI2puis ressort enI3sous l"incidencei. Les valeurs deNetnsont telles que la r´eflexion soit totale enI2.1)´Ecrire la relation deSnell-Descartesaux pointsI1etI3.
2)Quelles relations v´erifient les anglesretα;αetβ?
3)Quelle relation v´erifientNetnpour que la r´eflexion soit limite enI2?
CalculerN,r,α,βetipourn=3
2quand cette condition limite est r´ealis´ee.
On appelleN0cette valeur limite deN. Pour que la r´eflexion soit totale enI2,Ndoit-il ˆetre plus grand ou plus petit queN0?4)´Ecrire la relation v´erifi´ee parNetnpour que l"angleisoit nul. Que vautN?
Solution Ex-O1.4
1)νR= 4,568.1014Hz,νB= 6,167.1014Hz.
Les fr´equences ne d´ependent pas du milieu.2)c=c0
n, et donc :λ=cν=c0ν1n=λ0n. •Dans le verre de crown : cR= 1,993.108m.s-1
etλR= 436,3nm. •Dans le verre de flint : cR= 1,86.108m.s-1
etλR= 407,1nm.3)a) Le rayon r´efract´e est dans le plan d"in-
cidence etnsini=n?sinr. b)•Pour le verre de crown : rR= 35,16◦etrB= 34,71◦: le rayon bleu
est plus d´evi´e que le rayon rouge. L"angle entre le rayon rouge et le rayon bleu vautΔr= 0,45◦
•Pour le verre de flint : rR= 32,50◦etrB= 31,22◦: le rayon bleu
est plus d´evi´e que le rayon rouge. L"angle entre le rayon rouge et le rayon bleu vautΔr= 1,28◦
c)→Le" flint » est un verre plus dispersif que le " crown » car l"angle entre les deux rayons est le plus important. qadripcsi@aol.comhttp ://pcsi-unautreregard.over-blog.com/3Exercices d"Optique2008-2009
Solution Ex-O1.5
1)nn"a pas d"unit´e, doncAn"a pas d"unit´e
etBa la mˆeme unit´e queλ2,i.ele m`etre carr´e (m2).2)n(λ) n"est pas une fonction affine, en
revanchen?1λ2?est une fonction affine d"or-
donn´ee `a l"origineAet de coefficient directeur B.3)A= 1,468
etB= 5,2.10-15m2.4)n(633nm) = 1,468 +5,2.10-15
(633.10-9)2 soitn= 1,481Solution Ex-O1.8
1)Par application du principe du retour in-
verse de la lumi`ere, l"oeil du poisson voit la zone de l"espace d"o`u il peut ˆetre vu.Le poisson voit donc tout l"espace situ´e dans
l"air au travers d"un cˆone de sommet son oeil et de demi-angle au sommet ´egal `a l"angle li- mite de r´efraction pour le dioptre Eau/Air. En dehors de ce cˆone, il y a r´eflexion totale.2)il= arcsinnairneau= arcsin11,33≈49◦, le poisson voit donc l"espace situ´e au-del`a de la surface de l"eau sous un cˆone d"angle 98 dont l"intersection avec la surface de l"eau est un disque de rayonr.Avec tanil=r
h, on ah=rtanil= 2,6m.Solution Ex-O1.10
1)EnI, l"incidence ´etant normale, le rayon
incident n"est pas d´evi´e.Par contre, enJ, l"angle d"incidence esti=
45◦. Or l"´enonc´e dit que le rayon est transmis sini=⎷2 = 1,414.
2)EnJon ansini= sinr,
donc :n=sinr sini=⎷2 sinr. On peut calculerr`a l"aide des donn´ees fournies par la tache lumineuse sur l"´ecranE.Dans le triangleJKP,
tan(r-i) =KP JK=l 2-zl 2= l-2z l.Ainsi,r=i+ arctan?l-2z
l? et donc : n=⎷2 sin?
i+ arctan?l-2zl??3)n= 1,36 (´ethanol peut-ˆetre).
Solution Ex-O1.11
1)EnI1:Nsin45◦=N⎷2
2=nsinr1?
et enI3,nsinβ= sini 2?.2)La normale `aBCet la normale `aAB
sont perpendiculaires entre elles. dans le tri- angle form´e par ces normales etI1I2, on a : r+α=π 23?.De plus, avec le triangleI2CI3, on ´etablit :
44?.3)•La condition de r´eflexion (avec
ph´enom`ene de r´efraction) limite enI2s"´ecrit : nsinα= 15?Grˆace `a1?et3?, la relation5?conduit `a :
N2= 2(n2-1)
6?. •AN :N≡N0= 1,58r≡r0= 48,19◦ α=α0= 41,81◦β= 3,19◦i= 4,79◦ •Pour que la r´eflexion soit totale enI2, il faut que l"angleαsoit plus grand que l"angle d"in- cidence pour la r´efraction limiteα0que l"on vient de calculer (car alors la loi deDescartes pour la r´efractrion n"est plus v´erifi´ee :5?de- vientnsinα >1).Alors3??r < r0, et donc1??N < N0
ce qui revient `a direN 2(n2-1).4)Siiest nul, alorsβest nul, soitα=r=π
4, et donc1??N=n, soit :N=n=3 24http ://pcsi-unautreregard.over-blog.com/qadripcsi@aol.com
2008-2009Exercices d"Optique
DL no1 - La fibre optique
1. Att´enuation dans la fibre
Les pertes par transmission (not´eesX) sont exprim´ees en dB.km-1. On rappelle queXdB=10 log
P2 P1, avecP1puissance optique`al"entr´ee de la fibre etP2puissance optique au bout d"unkilom`etre de parcours. Vers 1970, l"att´enuation ´etait de 10dB.km-1. Actuellement, on arrive `a
0,005dB.km-1. Dans les deux cas, exprimer en % les pertes au bout d"un km.
2. Profil d"indice
Une fibre optique est g´en´eralement constitu´ee d"un coeur de rayon a dont l"indicenvarie avec la distancer`a l"axe, et d"une gaine d"indice constant n2. On suppose que :
n2(r) =n21(1-2Δ.(ra)α) pourr < an2(r) =n22poura < r < b a bn(r) On 2 avecn2< n1,αconstante positive,brayon ext´erieur de la gaine et Δ =n21-n222n21.Dans la pratique,n1etn2ont des valeurs tr`es voisines et Δ est tr`es petit, en g´en´eral Δ≈10-2.
→Repr´esentern=f(r) pourα= 1 ,α= 2 etαinfini.3. Fibre `a saut d"indice
On envisage le cas d"une fibre `a saut d"indice (αinfini)1.quotesdbs_dbs12.pdfusesText_18[PDF] les lois de descartes pour la reflexion
[PDF] les lois de descartes relatives à la réfraction
[PDF] les lois de descartes seconde
[PDF] les lois de descartes sur la réfraction
[PDF] les lois de snell descartes pdf
[PDF] les lois sur la cybercriminalité
[PDF] les lois sur la décentralisation au cameroun
[PDF] les lois sur la laicité
[PDF] les lois sur la laicité en france
[PDF] les lois sur la parité
[PDF] les lois sur la santé
[PDF] les lois sur le handicap
[PDF] les lois sur le handicap en france
[PDF] les loisirs des jeunes français