Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
Comme pour les graphes non orientés une façon (naïve) de déterminer si un graphe orienté est fortement connexe consiste à calculer sa fermeture transitive : si
 Les graphes BTS SIO2
Les graphes BTS SIO2
c) Fermeture transitive d'un graphe. 3. Graphes valués a) Définition b) Chemin minimal – chemin maximal. 4. La méthode Per. Page 2. 1. Graphes simples orientés.
 Algorithmique des graphes - 3 — Graphes orientés suite
Algorithmique des graphes - 3 — Graphes orientés suite
Entrées : un graphe orienté connexe G. Sortie : la fermeture transitive de G. 1 F ← GrapheOrienté(G.sommets());. 2 pour
 Algorithmes en Java Chap. 5 : Graphes
Algorithmes en Java Chap. 5 : Graphes
11 nov. 2013 Résultat : FT fermeture transitive du graphe. Algorithme 9 : FermetureTransitive ... Un graphe valué est un graphe orienté muni d'une application ...
 Algorithmique Contrôle no 4 (C4)
Algorithmique Contrôle no 4 (C4)
28 févr. 2022 ... fermeture transitive d'un graphe. Écrire la fonction CCFromWarshall ... connexe du sommet x dans le graphe orienté G. Choisissez la version ...
 Graphes orientés (§12.4) Terminologie Parcours darbres orientés
Graphes orientés (§12.4) Terminologie Parcours darbres orientés
Algorithme FloydWarshall(G). Entrée graphe orienté G. Sortie fermeture transitive G* de G i 1 pour tout v G.sommets() numéroter v par vi.
 Liens entre probl`emes de plus courts chemins de fermeture
Liens entre probl`emes de plus courts chemins de fermeture
22 mai 2007 2.1 Fermeture transitive d'un graphe orienté . . . . . . . . . . . . 4. 2.2 Fermeture transitive d'une matrice booléenne . . . . . . . . . 4.
 Algorithmique de graphes
Algorithmique de graphes
Un graphe non orienté est dit simple s'il est sans boucle et s'il n'existe pas Déterminer la fermeture transitive du graphe réduit Gr qui est sans circuit.
 Algorithmique Contrôle no 4 (C4)
Algorithmique Contrôle no 4 (C4)
1 mars 2017 Figure 1 – Graphe orienté. 1. Représenter ... — L'algorithme de Warshall calcule la matrice d'adjacence de la fermeture transitive d'un graphe.
 Exemple de calcul de fermeture transitive avec les matrices
Exemple de calcul de fermeture transitive avec les matrices
Voici le graphe pour lequel on se propose de calculer la fermeture transitive en calculant les puissances successives des matrices.
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
orienté alors il existe un chemin élémentaire de u vers v. idem
 Graphes orientés (§12.4) Terminologie Parcours darbres orientés
Graphes orientés (§12.4) Terminologie Parcours darbres orientés
Algorithme FloydWarshall(G). Entrée graphe orienté G. Sortie fermeture transitive G* de G i 1 pour tout v G.sommets() numéroter v par vi.
 Algorithmique de graphes
Algorithmique de graphes
4.4. Tri topologique dans un graphe orienté sans circuit . . . . . . . . . . . . . . . . . . . 16. 4.5. Fermeture transitive d'un graphe .
 Liens entre probl`emes de plus courts chemins de fermeture
Liens entre probl`emes de plus courts chemins de fermeture
13?/04?/2009 aussi la fermeture transitive de graphe orienté acyclique de graphe non orienté (cela revient au calcul des composantes connexes)
 TD 2 : Fermeture transitive
TD 2 : Fermeture transitive
Dessinez la fermeture transitive des graphes suivants : Soit G un graphe orienté sans circuit. Montrer qu'il existe un unique graphe G qui soit ?-.
 Travaux Dirigés
Travaux Dirigés
Donner le nombre d'arêtes d'un graphe non orienté complet de n sommets. Fermeture transitive d'un graphe G=(XU) orienté et composantes fortement.
 Liens entre probl`emes de plus courts chemins de fermeture
Liens entre probl`emes de plus courts chemins de fermeture
de fermeture transitive et de multiplication de matrices. Bertrand Marc. 22 mai 2007. Table des mati`eres 2.1 Fermeture transitive d'un graphe orienté .
 Aujourdhui Exemple PARTITION Les graphes
Aujourdhui Exemple PARTITION Les graphes
14?/12?/2009 permet de construire la fermeture transitive d'un graphe orienté ou non orienté. Algorithme de Warshall. • À partir de la matrice d'adjacence A ...
 Algorithmique des graphes
Algorithmique des graphes
un chemin est une cha?ne dont tous les arcs sont orientés ”dans le même sens”. Définitions. – Fermeture transitive la fermeture transitive d'un graphe
 Clôture transitive - University of Paris-Est Marne-la-Vallée
Clôture transitive - University of Paris-Est Marne-la-Vallée
UMLV 541 Problème G = (S A) graphe (orienté) Calculer H = (S B) où B est la clôture réflexive et transitive de A Note: (st) ? B ssi il existe un chemin de s à t dans G
 Fermeture transitive d'un graphe - techiedelightcom
Fermeture transitive d'un graphe - techiedelightcom
• Fermeture transitive • Explication de l’algorithme de Warshall Un graphe orienté pondéré est un graphe orienté muni d’une
 Algorithmique des graphes
Algorithmique des graphes
La fermeture transitive d’un graphe G=(SA) est un graphe G* avec les même sommets S mais dans lequel il existe un arc entre x et y si et seulement si il y a un chemin de x à y dans G
 1 Fermeture transitive de graphe
1 Fermeture transitive de graphe
1 Fermeture transitive de graphe Lebutducalculdelafermeturetransitived’ungrapheestdedéterminer pour tout couple de sommets s’il existe un chemin reliant le premier au second Unalgorithmee?cace(en( n3))estlesuivant: Algorithme 1 Fermeture-efficace(G) 1 soit n le nombre de sommets de G 2 soit M la matrice d’adjacence de G
 Searches related to fermeture transitive d+un graphe orienté PDF
Searches related to fermeture transitive d+un graphe orienté PDF
Le but de ce TP est de calculer la fermeture transitive d’un graphe orient´e D puis de l’utiliser a?n de calculer les composantes fortement connexes de D Langage Programme en c++ Votre programme pourra commencer par : #include #include using namespace std; const int n=6; int adjacence[n][n]={{000101} //La
Comment trouver la fermeture transitive sur un graphe de composants fortement connectés ?
Ainsi, le problème réduit la recherche de la fermeture transitive sur un graphe de composants fortement connectés, qui devrait avoir considérablement moins d'arêtes et de sommets que le graphe donné. On sait qu'on peut trouver tous les sommets accessibles depuis un sommet v en appelant Recherche en profondeur d'abord (DFS) sur le sommet v.
Qu'est-ce que le graphe orienté ?
correspond à l’une des contraintes. Plus précisément, le graphe orienté associé au Le sommet est ajouté de telle sorte que tous les autres sommets soient joignables à partir de . solution. Soit un graphe orienté ou non orienté et soit un sommet de quelconque. On désigne par la distance du plus court chemin joignant à .
Comment trouver la fermeture transitive d'une matrice de connectivité ?
Notez que tous les éléments diagonaux de la matrice de connectivité sont 1 puisqu'un chemin existe de chaque sommet à lui-même. Comme indiqué dans le post précédent, nous pouvons utiliser le Algorithme de Floyd-Warshall pour trouver le fermeture transitive d'un graph avec V sommets dans O (V3) temps.
Qu'est-ce que la fermeture transitive d'un digraphe ?
La fermeture transitive d'un digraphe G est un digraphe G’ avec un bord (i, j) correspondant à chaque chemin dirigé depuis i à j dans G. Le digraphe résultant G’ La représentation sous forme de matrice d'adjacence est appelée matrice de connectivité.
14/12/2009
et structuresdedonnéesavancés 11PatrickReuter
http://www.labri.fr/~preuter/asda2009 surrécurrenceetTD8Siteweb/solutions
Dictionnaires
Lesarbres
quipèsentp 1 ,p 2 ,...,p n grammes. •Cethommeàdeuxenfants ensemblesdisjointspourquelasommedespoids desdeuxsousͲensemblessoitégal?Ils'agitduproblèmePARTITIONPARTITION
•Commenttrouverlespartitions? lessommesdesdeuxpoidssontégales?graphes
-UnensembleV(G)={v1 ,v 2 ,...,v n }desommets(anglais: onevertex,twovertices)14/12/2009
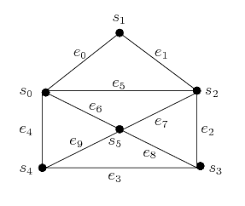
•Orientation: -lesgraphesnonorientés -lesgraphesorientés •degré •boucle •parité(sommetspairsetimpairs) •adjacence,voisinetvoisinage sommetisolésommetisolé •sousͲgraphe,clique •Isomorphisme •Chaîne,sousͲchaîne •Cycle •Grapherégulier •Graphecomplet •Grapheconnexe d'adjacence •SoitG=(V,E)avecV={s 1 ,s 2 ,...,s n 1si(s i ,s k )E,A i,k =0sinon decontacts descontacts...PatrickPetra
d'adjacence pourchaquesommetpourchaquesommetMatriced'adjacence
0 1 0 0 0 0 0
1 0 1 0 0 0 0
0 1 0 1 1 0 0
Patrick(1)
Jérôme(5)Petra(4)
(7) APierre(2)Clémentine(3)
(6)1:montrerlescontactsdirects
Entrée : Graphe G définie par une matrice d'adjacence A et un sommet s défini par son indice
fonction montrerContacts(s) début pour i de 1 à nbSommets(G) si(i s ET A[s][i]=1) alors afficher nom[i] à l' fin si fin pour fin { Montrer les conacts directs }14/12/2009
unsommetadéjàétévisité2:montrerlescontactsetles
contactsdescontactsEntrée : Graphe G définie par une matrice d'adjacence A et un sommet s défini par son indice
fonction montrerContacts(s)Début
marquerSommet(s) pour i de 1 à nbSommets(G) si (i s ET A[s][i]=1 ET NOT marqué(i)) alors afficher nom[i] à l' fin si fin pour fin { Montrer les contacts directs et les contacts des contacts directs }Etape2:montrerlescontactsetles
contactsdescontactsEntrée : Graphe G définie par une matrice d'adjacence A et un sommet s défini par son indice
fonction montrerContacts(s : integer) début marquerSommet(s) pour i de 1 à nbSommets(G) si (i s ET A[s][i]=1 ET NOT marqué(i)) alors pour j de 1 à nbSommets(G) si (j s ET A[i][j]=1 ET NOT marqué(j)) alors marquerSommet(j); afficher nom[j] à l'écran fin si fin pour fin si fin pour fin { Montrer les contacts directs et les contacts des contacts directs }Etape3:Reconnaîtrelarécursivité
fonction montrerContacts(s : integer) début marquerSommet(s) pour i de 1 à nbSommets(G) si (i s ET A[s][i]=1 ET NOT marqué(i)) alors afficher nom[i] à l'écran pour j de 1 à nbSommets(G) si (j s ET A[i][j]=1 ET NOT marqué(j)) alors marquerSommet(j); afficher nom[j] à l'écran fin si fin pour fin si fin pour fin { Montrer les contacts directs et les contacts des contacts directs }Etape4:Récursivité
Entrée : Graphe G définie par une matrice d'adjacence A et un sommet s défini par son indice
fonctionmontrerContacts(s : integer)Début
marquerSommet(s); pour i de 1 à nbSommets(G) si (i s ET A[s][i]=1 ET NOT marqué(i)) alors fin si fin pour fin { Montrer les conacts directs et les contacts des contacts directs }Vérificationdesdeuxconditionsd'un
algorithmerécursif nepass'appelerinfiniment -Quandtouslessommetsvoisinsd'unsommet14/12/2009
d'adjacence0 1 0 0 0 0 0
1 0 1 0 0 0 0
0 1 0 1 1 0 0
Patrick(1)
Jérôme(5)Petra(4)
(7) APierre(2)Clémentine(3)
(6) transitiveGrapheG*
+=(V,E*+),oùunearête(i,j)̿E+ssi ilyaunechaînedeiàj. transitiveetréflexiveG*. transitive1 1 1 1 1 0 0
1 1 1 1 1 0 0
1 1 1 1 1 0 0
•A:Matriced'adjacenceFermeturetransitive
Matriced'adjacencedelafermeture
transitive •G(V,E):(Matriced'adjacenceA): -A i,k =1si(s i ,s k )E,A i,k =0sinon d'adjacenceA*) -A* i,k =1ssiilyaunechaînedes i às k pourlecalculscientifique -Maple -Matlab -Mupad -Scilab14/12/2009
deWarshall d'ungrapheorientéounonorienté.AlgorithmedeWarshall
•OnsupposequeA k Ͳ1 OU(A kͲ1 ETA kͲ1 •Matriced'adajcencedeG*:A n [i,j]AlgorithmedeWarshall
Entrée:Matriced'adjacenceA
pourk de 1 à |V(G)| faire pouri de 1 à |V(G)| faire pourj de 1 à |V(G)| faireA[i][k]=1 ET A[k][j]=1))
A[i][j]=1
elseA[i][j]=0
A[i][j] = A[i][j] OU (A[i][k] ET A[k][j])
deWarshall •Complexité -O(n 3 transitived'dungrapheunefoispourtoute, onpeutsavoirsilessommetss i ets j appartiennentà •Commenttestersiun grapheestconnexe? marquerSommet(s) visite[s]=truePOURtouslesvoisinsidesFAIRE
visite[i]==falseALORS marquerSommet(i)14/12/2009
•Dictionnaires desclés "associativearray" •Rappel:PHP... MySQLParcourirlesenregistrenents
Dictionnaires •fa ={} •fa['salut']="hello" •fa['oui']="yes" •fa['non']="no" différencequ'ilssontnonmodifiables référencesréférences descrochets14/12/2009
différencequ'ilssontnonmodifiables référencesréférences descrochetsTuples
>>> x = (1,2,3) >>> x (1, 2, 3) >>> x[2]Théoriedelacomplexité
ClassesdeGrandͲO
•O(1) complexitéconstante •O(logn)complexitélogarithmique •O(n) complexitélinéaire •O(nlognquasͲlin •O(n a) complexitépolynomiale -O(n 2) complexitéquadratique -O(n 3) complexitécubique •O(a n) complexitéexponentielle •O(n! complexitéfactorielle n)O(n)O(nlogn)O(n 2 )O(n 3 )O(a n )O(n!) delacomplexité-Changementdelafonction
2èmesolution
changerlafonction •O(logn) logarithmique O(n) •O(n) linéaire •O(nlogn)QuasiͲlinéaire
•O(n 2) quadratique •O(n 3) cubique •O(a n) exponentiel nInformatiquethéorique
•Théoriedecomplexité •Théoriedecalculabilité14/12/2009
quipèsentp 1 ,p 2 ,...,p n grammes. •Cethommeàdeuxenfants ensemblesdisjointspourquelasommedespoids desdeuxsousͲensemblessoitégal?Ils'agitduproblèmePARTITION
PARTITION
•Commenttrouverlespartitions? lessommesdesdeuxpoidssontégales? decomplexité eninformatique lldi idlhé idl•Esedistdelatdela calculabilité pasêtrerésoluparunordinateur.Théoriedecomplexité
effectivementêtrerésolus,Savoirs'silyaunesolutionefficaceense
basantsuruneestimation(théorique) -desbesoinsenmémoireinformatique (complexitédemémoire)Théoriedecomplexité
•Unproblèmeformalisédelamanièresuivante :éventuellementuncalcul).
problèmesdedécisionbinaire (réponsesoitouiou non) decomplexité •Cependant: d' •Eneffet,ilestfaciledetransformerun problèmed'optimisationenproblèmede décision.14/12/2009
decomplexité valeurn titlblèddé i iiità-ontraleprodedécquconsà comparernàuncertaink. -Entraitantplusieursvaleursdekonpeut déterminerunevaleuroptimale. TSP TSP- TravelingSalesmanProblem(Problèmeduvoyageurdecommerce)étantdonné
retlesdistancesséparantchaquesommet, (nͲ1)!Possibilités!Grapheorientéponderé
•G=(V,E,ʔ)0 64 94
A = 64 0 47 7894 47 0 65 197
78 65 0 193
197 193 0
TSP TSP- TravelingSalesmanProblem(Problèmeduvoyageurdecommerce)étantdonné
retlesdistancesséparantchaquesommet, (nͲ1)!Possibilités! •TSPmétrique:Onpeutpasserplusieursfoisparlememe
sommet14/12/2009
Données :
tEbld' ttquotesdbs_dbs44.pdfusesText_44[PDF] fermeture transitive matrice
[PDF] décomposition d'un graphe en niveaux
[PDF] chemin hamiltonien
[PDF] de l'année 1789 ? l'exécution du roi cm1
[PDF] graphe d'ordonnancement
[PDF] sujet algorithme bts sio corrigé
[PDF] calcul matrice booléenne
[PDF] calcul matriciel bts
[PDF] prise de note rapide tableau abréviations
[PDF] sauzay programme
[PDF] programme voltaire
[PDF] un petit paragraphe sur l'environnement
[PDF] exemple de texte argumentatif sur l'environnement
[PDF] texte sur l'environnement