[PDF] fourier transform of triangle

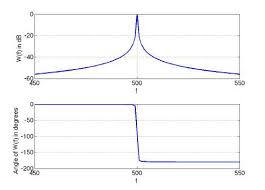
2.2 Fourier transform and spectra

2.2 Fourier transform and spectra. Example 2-7. Spectrum of a triangular pulse w(t)= Λ(t /T). Find the spectrum of a triangular pulse. 2. (). ( ). (. ) t wt. W 

AN ACCURATE CONFORMAL FOURIER TRANSFORM METHOD

A curved triangular mesh combined with curvilinear coordinate transformation is adopted to flexibly model an arbitrary shape of the discontinuity boundary. This 

Table of Fourier Transform Pairs

The rectangular function is an idealized low-pass filter and the sinc function is the non-causal impulse response of such a filter. 12 tri is the triangular 

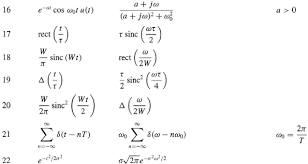Lecture 10 - Fourier Transform

08-Feb-2011 ◇ A unit triangle function A(x):. ◇ Interpolation function sinc(x): or. L7.2-1 p687. Page 2. Lecture 10 Slide 5. PYKC 8-Feb-11. E2.5 Signals ...

Lecture 2: 2D Fourier transforms and applications

Much of this material is a straightforward generalization of the 1D Fourier analysis with which you are familiar. Page 2. Reminder: 1D Fourier Series. Spatial 

14. The Fourier Series & Transform

transform of a triangle function. Sinc2(ax) is the diffraction pattern from a slit. It just crops up everywhere Page 23. The Fourier Transform of the ...

ECE 45 Homework 3 Solutions

Note: the function ∆(t) is sometimes called the unit triangle function as Therefore

Fourier Transforms

% Fourier Transform of triangular pulse clearclf syms x t w X1 Xrect tau title('Compare triangle and rectangle X(omega) P121'). Fourier Transform. Page ...

EE 261 - The Fourier Transform and its Applications

Fourier coefficients. However it's not only a discontinuity that forces high frequencies. Take a triangle wave

A New Representation of FFT Algorithms Using Triangular Matrices

It was 50 years ago when Cooley and Tukey proposed the fast Fourier transform (FFT) algorithm [1]. The FFT is a way to compute the discrete Fourier transform ( 

Lecture 10 - Fourier Transform

Feb 8 2011 Definition of Fourier Transform. ? The forward and inverse Fourier Transform are defined for aperiodic ... A unit triangle function A(x):.

Table of Fourier Transform Pairs

Fourier Transform F(w). Definition of Inverse Fourier Transform tri is the triangular function. 13. Dual of rule 12.

14. The Fourier Series & Transform

Fourier Series & The Fourier Transform. What is the Fourier Transform? Anharmonic Waves The triangle function is just what it sounds like.

ECE 45 Homework 3 Solutions

Problem 3.1 Calculate the Fourier transform of the function the unit triangle function as it a triangular pulse with height 1

Lecture 13: Discrete Time Fourier Transform (DTFT)

Mar 9 2017 Lecture 13: Discrete Time Fourier Transform. (DTFT) ... Example: DTFT of a Triangle ... inverse

Chapter2 copy.pptx

Where f[*] denotes the Fourier transform of [*] and f is the frequency parameter with units of hertz (i.e.

EE 261 – The Fourier Transform and its Applications

EE 261 The Fourier Transform and its Applications Fall 2007

e2?ikt = sin(2?t(N + 1/2)) sin(?t) . 2. Some practice combining simple signals. (5 points each). The triangle function with a parameter a > 0 is. ?a 

Fourier Transforms

3.4 Fourier Transform. • Definition (Equation 3.30) For b ? 0 does not have a Fourier transform in ... Fourier Transform of triangular pulse clearclf.

Lecture 8 ELE 301: Signals and Systems

Linearity Theorem: The Fourier transform is linear; that is given two Fourier transform X(f ) as its output