 SEN301 OPERATIONS RESEARCH I PREVIUOS EXAM
SEN301 OPERATIONS RESEARCH I PREVIUOS EXAM
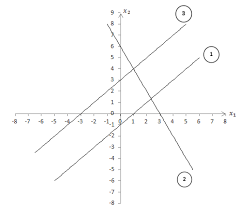
Formulate the problem of deciding how much to produce per week as a linear program. 2. Answer the questions related to the model below: max. 3 x1 + 2 x2 st. 2
 DEPARTMENT OF MECHANICAL ENGINEERING BM7002
DEPARTMENT OF MECHANICAL ENGINEERING BM7002
BM7002-OPERATIONS RESEARCH. QUESTION BANK. UNIT 1 – Linear Models. PART – A (2 Marks). 1. Define Operations Research? 2. What is linear programming? 3. What are
 OPERATIONS RESEARCH Multiple Choice Questions
OPERATIONS RESEARCH Multiple Choice Questions
develop the initial solution to the transportation problem. C. assist one in moving from an initial feasible solution to the optimal solution. D. determine
 Unit : 1
Unit : 1
Question Bank. Unit : 1. Introduction of Operations Research and Linear Programming. Q : 1 Short Answer Questions: 1. Write the definition of operation research
 UNIT I Operation Research UNIT II Linear Programming Problems
UNIT I Operation Research UNIT II Linear Programming Problems
Operation Research. Short Answer Questions: 1. Define Operations Research. (CO1). 2. What are the three phases of the scientific method on which OR approach
 Question Bank Subject: Operations research (EOE-073) Unit-I
Question Bank Subject: Operations research (EOE-073) Unit-I
Q8- Determine an initial basic feasible solution to the following transportation problem by using North-West corner rule. To. D1. D2. D3. D4. D5. From A. B. C.
 OPERATIONS RESEARCH Multiple Choice Questions
OPERATIONS RESEARCH Multiple Choice Questions
develop the initial solution to the transportation problem. B. assist one in moving from an initial feasible solution to the optimal solution. C. determine
 Operation Research.pdf
Operation Research.pdf
The fourth characteristic of operation research which is often overlooked
 Multiple Choice Questions BCA IV Sem OPERATIONS RESEARCH
Multiple Choice Questions BCA IV Sem OPERATIONS RESEARCH
Who defined Operations Research as scientific approach to problem solving for executive a given problem and also derives a solution from the model using ...
 SEN301 OPERATIONS RESEARCH I PREVIUOS EXAM
SEN301 OPERATIONS RESEARCH I PREVIUOS EXAM
solution (dual variables value and dual objective function value) without solving the dual model. INFORMATION FOR QUESTIONS 14-25. LP Model for “Modified
 Operations Research Second Edition
Operations Research Second Edition
Multiple choice question and answers . The subject OPERATIONS RESEARCH is a branch of mathematics - specially applied mathematics.
 UNIT I 1 INTRODUCTION TO OPERATIONS RESEARCH LESSON
UNIT I 1 INTRODUCTION TO OPERATIONS RESEARCH LESSON
Operations Research can also be treated as science in the sense it describing bad answers to problems which otherwise have worse answers”.
 Problems and exercises in Operations Research
Problems and exercises in Operations Research
29 Nov 2006 Problems and exercises in Operations Research. Leo Liberti1. Last update: November 29 ... 12.4 The travelling salesman problem: Solution .
 Multiple Choice Questions OPERATIONS RESEARCH
Multiple Choice Questions OPERATIONS RESEARCH
15. Operations Research uses models built by quantitative measurement of the variables concerning a given problem and also derives a solution from the model
 56:171 Operations Research Final Examination Solutions
56:171 Operations Research Final Examination Solutions
56:171 Operations Research If in the optimal primal solution of an LP problem (min cx st Ax?b
 Unit : 1
Unit : 1
Write the definition of operation research. 2. Write the definition of solution basic solution. 3. What is Linear programming problem?
 Designing HIV/AIDS Intervention Studies: An Operations Research
Designing HIV/AIDS Intervention Studies: An Operations Research
counseling and testing stigma
 OPERATIONS RESEARCH Multiple Choice Questions
OPERATIONS RESEARCH Multiple Choice Questions
develop the initial solution to the transportation problem. C. assist one in moving from an initial feasible solution to the optimal solution. D. determine
 Malaria and Covid-19 Operations Research Questions Background
Malaria and Covid-19 Operations Research Questions Background
Malaria Operations Research (OR) is critical to the implementation of malaria It provides responses/answers to implementation challenges/questions.
 Review Solutions Exam 2 Operations Research - Whitman College
Review Solutions Exam 2 Operations Research - Whitman College
Review Solutions Exam 2 Operations Research 1 Prove the weak duality theorem: For any x feasible for the primal and y feasible for the dual then HINT: Put the primal so that Ax b and the dual so that ATy c SOLUTION: With the primal and dual in normal form then yTAx y Tb and xTA y xTc Noting that x TA y = (Ax)Ty = y (Ax) we get that:
 Operations Research and Networks
Operations Research and Networks
56:171 Operations Research Final Exam '98 page 11 of 14 For $20000 Sue can hire a consultant who will predict the outcome of the trial i e either he predicts a loss of the suit (event PL) or he predicts a win (event PW) The consultant predicts the correct outcome 80 of the time 2
 Principles and Applications of Operations Research
Principles and Applications of Operations Research
This chapter will provide an overview of Operations Research (O R ) from the perspective of an industrial engineer The focus of the chapter is on the basic philosophy behind O R and the so-called “O R approach” to solving design and operational problems that industrial engineers commonly encounter
 OPERATIONS RESEARCH Multiple Choice Questions
OPERATIONS RESEARCH Multiple Choice Questions
The Operations research technique which helps in minimizing total waiting and service costs is Queuing Theory Decision Theory Both A and B None of the above UNIT II LINEAR PROGRAMMING PROBLEMS 23 What is the objective function in linear programming problems? A constraint for available resource
 Searches related to operation research questions and answers pdf filetype:pdf
Searches related to operation research questions and answers pdf filetype:pdf
Operations Research started just before World War II in Britain with the establishment of teams of scientists to study the strategic and tactical problems involved in military operations A True B False 8 OR can be applied only to those aspects of libraries where mathematical models can be prepared A True B False 9
 [PDF] sen301 operations research i previuos exam questions
[PDF] sen301 operations research i previuos exam questions
SEN301 OPERATIONS RESEARCH I PREVIUOS EXAM QUESTIONS 1 A company is involved in the production of two items (X and Y) The resources need to produce X
 QUESTION BANK ON OPERATIONS RESEARCH UNIT-1: Basics of
QUESTION BANK ON OPERATIONS RESEARCH UNIT-1: Basics of
Download Free PDF Explain the meaning of linear programming problem stating its uses and give Formulate the problem as a linear programming problem
 [PDF] OPERATIONS RESEARCH Multiple Choice Questions
[PDF] OPERATIONS RESEARCH Multiple Choice Questions
Multiple Choice Questions 1 Operations research is the application of -------to a problem within a system to yield the optimal solution
 [PDF] Problems and exercises in Operations Research - LIX-polytechnique
[PDF] Problems and exercises in Operations Research - LIX-polytechnique
29 nov 2006 · Problems and exercises in Operations Research 9 Linear programming: Solutions 12 4 The travelling salesman problem: Solution
 Operation Research MCQ Quiz Questions & Answers PDF Download
Operation Research MCQ Quiz Questions & Answers PDF Download
In this blog we have listed 30 Operation Research objective questions and answers The Operation Research questions is most important section and commonly asked
 [PDF] Operations Research Second Edition
[PDF] Operations Research Second Edition
1 2 HISTORY OF OPERATIONS RESEARCH Operations Research is a 'war baby' It is because the first problem attempted to solve in a
 [PDF] Operations Research Problems
[PDF] Operations Research Problems
This book includes an overview of each topic considered with worked examples in the text problems solutions to prob- lems end-of-chapter references and Index
 [PDF] BM7002-OPERATIONS RESEARCH QUESTION BANK UNIT 1
[PDF] BM7002-OPERATIONS RESEARCH QUESTION BANK UNIT 1
1 Define Operations Research? 2 What is linear programming? List out the methods used to obtain initial basic feasible solution in Transportation
 Operations Research MCQ [Free PDF] - Objective Question Answer
Operations Research MCQ [Free PDF] - Objective Question Answer
20 avr 2023 · Get Operations Research Multiple Choice Questions (MCQ Quiz) with answers and detailed solutions Download these Free Operations Research
What are the principal operations research (or) tools?
- Introduction This volume presents the principal operations research (OR) tools that help in the planning and management of all sorts of networks. The term “network” is to be understood in a very broad sense. In effect, this term also designates physical networks, such as road or railway networks, as well as logical networks, used for
Who is the author of Operations Research and networks?
- Operations Research and Networks Edited by Gerd Finke Series Editor Pierre Dumolard First published in France in 2002 by Hermes Science/Lavoisier entitled: “Recherche opérationnelle et réseaux: Méthodes d’analyse spatiale” First published in Great Britain and the United States in 2008 by ISTE Ltd and John Wiley & Sons, Inc.
What are the constraints in operations research and networks?
- Introduction written by Gerd FINKE. x Operations Research and Networks certain conditions (constraints). These constraints are linear (equations or inequations) and model the use of finite capacity resources, distance limits, budget restrictions, etc.
´Ecole Polytechnique
Problems and exercises in Operations Research
Leo Liberti
1Last update: November 29, 2006
1Some exercises have been proposed by other authors, as detailed in the text. All the solutions, however, are by the
author, who takes full responsibility for their accuracy (or lack thereof).ExercisesOperations Research L. Liberti
2Contents1 Optimization on graphs9
1.1 Dijkstra"s algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . 9
1.2 Bellman-Ford"s algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 9
1.3 Maximum flow . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 9
1.4 Minimum cut . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 10
1.5 Renewal plan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 10
1.6 Connected subgraphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
1.7 Strong connection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 11
2 Linear programming13
2.1 Graphical solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 13
2.2 Geometry of LP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 13
2.3 Simplex method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 14
2.4 Duality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 14
2.5 Geometrical interpretation of the simplex algorithm . . . . . . . . . . . .. . . . . . . . . 15
2.6 Complementary slackness . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 15
2.7 Sensitivity analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 15
2.8 Dual simplex method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 16
3 Integer programming17
3.1 Piecewise linear objective . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 17
3.2 Gomory cuts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 17
3.3 Branch and Bound I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 17
3.4 Branch and Bound II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 18
3.5 Knapsack Branch and Bound . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 18
3ExercisesOperations Research L. Liberti
4 Easy modelling problems19
4.1 Compact storage of similar sequences . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 19
4.2 Communication of secret messages . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 19
4.3 Mixed production . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 20
4.4 Production planning . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 20
4.5 Transportation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 21
4.6 Project planning with precedences . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4.7 Museum guards . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 22
4.8 Inheritance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 22
4.9 Carelland . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 23
4.10 CPU Scheduling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 23
4.11 Dyeing plant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 24
4.12 Parking . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 24
5 Difficult modelling problems25
5.1 Checksum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 25
5.2 Eight queens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 27
5.3 Production management . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 27
5.4 The travelling salesman problem . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 27
5.5 Optimal rocket control 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 28
5.6 Double monopoly . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 28
6 Telecommunication networks31
6.1 Packet routing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 31
6.2 Network Design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 31
6.3 Network Routing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 32
7 Nonlinear programming35
7.1 Error correcting codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 35
7.2 Airplane maintenance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 35
7.3 Pooling problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 36
7.4 Optimal rocket control 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 37
8 Optimization on graphs: Solutions39
CONTENTS4
ExercisesOperations Research L. Liberti
8.1 Dijkstra"s algorithm: Solution . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . 39
8.2 Bellman-Ford algorithm: Solution . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . 40
8.3 Maximum flow: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 40
8.4 Minimum cut: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 42
8.5 Renewal plan: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 43
8.6 Connected subgraphs: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 44
8.7 Strong connection: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 44
9 Linear programming: Solutions45
9.1 Graphical solution: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 45
9.2 Geometry of LP: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 47
9.3 Simplex method: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 51
9.4 Duality: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 53
9.5 Geometrical interpretation of the simplex algorithm: Solution . . . . .. . . . . . . . . . . 54
9.5.1 Iteration 1: Finding the initial vertex . . . . . . . . . . . . . . . . . . . .. . . . . 55
9.5.2 Iteration 2: Finding a better vertex . . . . . . . . . . . . . . . . . . . . . . .. . . 56
9.5.3 Iterazione 3: Algorithm termination . . . . . . . . . . . . . . . . . . . .. . . . . . 56
9.6 Complementary slackness: Solution . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 56
9.7 Sensitivity analysis: Solution . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . 57
9.8 Dual simplex method: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 58
10 Integer programming: Solutions61
10.1 Piecewise linear objective: Solution . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 61
10.2 Gomory Cuts: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 62
10.3 Branch and Bound I: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 65
10.4 Branch and Bound II: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 67
10.5 Knapsack Branch and Bound: Solution . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 67
11 Easy modelling problems: solutions71
11.1 Compact storage of similar sequences: Solution . . . . . . . . . . . . . . . .. . . . . . . . 71
11.2 Communication of secret messages: Solution . . . . . . . . . . . . . . . . . . .. . . . . . . 71
11.3 Mixed production: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 72
11.3.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 72
CONTENTS5
ExercisesOperations Research L. Liberti
11.3.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 73
11.3.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 73
11.4 Production planning: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 74
11.4.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 74
11.4.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 75
11.4.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 76
11.5 Transportation: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . 77
11.5.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 77
11.5.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 78
11.5.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 79
11.6 Project planning with precedences: Solution . . . . . . . . . . . . . . . . . . . . . . . . .. 79
11.7 Museum guards: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 80
11.7.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 80
11.7.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 80
11.7.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 81
11.8 Inheritance: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 82
11.8.1 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 82
11.8.2 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 83
11.9 Carelland: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 83
11.9.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 84
11.9.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 84
11.9.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 85
11.10CPU Scheduling: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 86
11.10.1AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 87
11.10.2CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 88
11.11Dyeing plant: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 88
11.11.1AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 89
11.11.2CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 90
11.12Parking: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . 90
11.12.1AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 91
11.12.2CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 92
CONTENTS6
ExercisesOperations Research L. Liberti
12 Difficult modelling problems: Solutions93
12.1 Checksum: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 93
12.1.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 93
12.1.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 94
12.1.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 95
12.2 Eight queens: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 96
12.2.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 96
12.2.2 AMPL model, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 97
12.2.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 97
12.3 Production management . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 98
12.3.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 98
12.3.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 99
12.4 The travelling salesman problem: Solution . . . . . . . . . . . . . . . . . . .. . . . . . . . 100
12.4.1 Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 100
12.4.2 AMPL model, data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 100
12.4.3 Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 101
12.4.4 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 103
12.4.5 Heuristic solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 103
12.5 Optimal rocket control 1: Solution . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . 105
12.5.1 AMPL: model, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 106
12.5.2 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 107
12.6 Double monopoly: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 108
13 Telecommunication networks: Solutions111
13.1 Packet routing: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 111
13.1.1 Formulation for 2 links . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 111
13.1.2 Formulation formlinks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
13.1.3 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 112
13.1.4 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 113
13.2 Network Design: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 113
13.2.1 Formulation and linearization . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 113
13.2.2 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 114
CONTENTS7
ExercisesOperations Research L. Liberti
13.2.3 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 116
13.3 Network Routing: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 117
13.3.1 AMPL model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 119
13.3.2 Soluzione di CPLEX . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 122
14 Nonlinear programming: Solutions123
14.1 Error correcting codes: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 123
14.2 Airplane maintenance: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 123
14.3 Pooling problem: Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 124
14.3.1 AMPL: model, data, run . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 125
14.3.2 CPLEX solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 127
14.4 Optimal rocket control 2: Solution . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . 127
CONTENTS8
Chapter 1Optimization on graphs1.1 Dijkstra"s algorithmUse Dijkstra"s algorithm to find the shortest path tree in the graph below using vertex 1 as source.
1 2 43 5 62
4 1 52038 3
1.2 Bellman-Ford"s algorithm
Check whether the graph below has negative cycles using Bellman-Ford"s algorithm and 1as a source vertex. 1 2 43 5 62
4 1 520-13-1
1.3 Maximum flow
Determine a maximum flow from node 1 to node 7 in the networkG= (V,A) below (the values on the arcs (i,j) are the arc capacitieskij). Also find a cut having minimum capacity. 9ExercisesOperations Research L. Liberti
12 345 7 66
6 1 33
7 54
411
1.4 Minimum cut
Find the mimum cut in the graph below (arc capacities are marked on the arcs). What algorithm did you use? st1 2433
10 744
3 2 883
1.5 Renewal plan
A small firm buys a new production machinery costing 12000 euros. In order to decrease maintenance costs, it is possible to sell the machinery second-hand and buy a new one. The maintenance costs and possible gains derived from selling the machinery second-hand are given below (forthe next 5 years): age (years) costs (keuro)gain (keuro) 02- 1 472 56
3 92
4 121
Determine a renewal plan for the machinery which minimizes the total operation cost over a 5-year period.
[E. Amaldi, Politecnico di Milano]1.6 Connected subgraphs
Consider the complete undirected graphKn= (V,E) whereV={0,...,n-1}andE={{u,v} |u,v? V}. LetU={imodn|i≥0}andF={{imodn,(i+2) modn} |i≥0}. Show that (a)H= (U,F) is a subgraph ofGand that (b)His connected if and only ifnis odd.Connected subgraphs10
ExercisesOperations Research L. Liberti
1.7 Strong connection
Consider the complete undirected graphKn= (V,E) and orient the edges arbitrarily into an arc setAso that for each vertexv?V,|δ+(v)| ≥1 and|δ-(v)| ≥1. Show that the resulting directed graph
G= (V,A) is strongly connected.
Strong connection11
ExercisesOperations Research L. Liberti
Strong connection12
Chapter 2Linear programming2.1 Graphical solutionConsider the problem min xcxAx≥b
x≥0 wherex= (x1,x2)T,c= (16,25),b= (4,5,9)T, and A=(( 1 7 1 5 2 3))1. Solve the problem graphically.
2. Write the problem in standard form. IdentifyBandNfor the optimal vertex of the feasible
polyhedron. [E. Amaldi, Politecnico di Milano]2.2 Geometry of LP
Consider the following LP problem.
maxz?= 3x1+ 2x2(?) x x1,x2≥0.
1. Solve the problem graphically, specifying the variable values andz?at the optimum.
2. Determine the bases associated to all the vertices of the feasible polyhedron.
13ExercisesOperations Research L. Liberti
3. Specify the sequence of the bases visited by the simplex algorithm to reach the solution (choosex1
as the first variable entering the basis).4. Determine the value of the reduced costs relative to the basic solutions associated to the following
vertices, expressed as intersections of lines inR2: (a) (Eq. 2.1)∩(Eq. 2.2); (b) ((Eq. 2.1)∩(Eq. 2.3),
5. Verify geometrically that the objective function gradient can be expressed asa non-negative linear
combination of the active constraint gradients only in the optimal vertex (keep in mind that the6. Say for which values of the RHS coefficientb1in constraint (2.1) the optimal basis does not change.
7. Say for which values of the objective function coefficients the optimal vertex is((x1= 0)∩(Eq. 2.2)),
wherex1= 0 is the equation of the ordinate axis inR2.8. For which values of the RHS coefficient associated to (2.2) the feasible region is (a) empty (b)
contains only one solution?9. For which values of the objective function coefficientc1there is more than one optimal solution?
[M. Trubian, Universit`a Statale di Milano]2.3 Simplex method
Solve the following LP problem using the simplex method: minz=x1-2x22x1+ 3x3= 1
3x1+ 2x2-x3= 5
x1,x2,x3≥0.
Use the two-phase simplex method (the first phase identifies an initial basis) and Bland"s rule (for a
choice of the entering and exiting basis which ensures algorithmic convergence). [E. Amaldi, Politecnico
di Milano]2.4 Duality
What is the dual of the following LP problems?
1. min x3x1+ 5x2-x3 x x≥0? ?(2.4) 2. min xx1-x2-x32x1-3x2-2x3≥4
x1-x3= 2
x1≥0
x2≥0?
?(2.5)Duality14
ExercisesOperations Research L. Liberti
3. max xx1-x2-2x3+ 32x1-3x2≥4x3
x1-x3=x2
x1≥0
x ?(2.6)2.5 Geometrical interpretation of the simplex algorithm
Solve the following problem
max xx1+x2 x1≥0
x using the simplex algorithm. Start from the initial point ¯x= (1,0).2.6 Complementary slackness
Consider the problem
max 2x1+x2 x x x1, x2≥0.
1. Write the dual problem.
2. Verify that ¯x= (20
3,113) is a feasible solution.
3. Show that ¯xis optimal using the complementary slackness theorem, and determine the optimal
solution of the dual problem. [Pietro Belotti, Carnegie Mellon University]2.7 Sensitivity analysis
Consider the problem:
minx1-5x2 x x1,x2≥0.?
1. Check that the feasible solutionx?= (4,9) is also optimal.
2. Which among the constraints" right hand sides should be changed to decrease the optimal objective
function value, supposing this change does not change the optimal basis? Should the change be a decrease or an increase?Sensitivity analysis15
ExercisesOperations Research L. Liberti
2.8 Dual simplex method
Solve the following LP problem using the dual simplex method. min 3x1+ 4x2+ 5x32x1+ 2x2+x3≥6
x1+ 2x2+ 3x3≥5
x1,x2,x3≥0.
What are the advantages with respect to the primal simplex method?Dual simplex method16
Chapter 3Integer programming3.1 Piecewise linear objectiveReformulate the problem min{f(x)|x?R≥0}, where:
f(x) =? 1 as a Mixed-Integer Linear Programming problem.3.2 Gomory cuts
Solve the following problem using Gomory"s cutting plane algorithm. minx1-2x2 x x≥0, x?Z2? [Bertsimas & Tsitsiklis,Introduction to Linear Optimization, Athena Scientific, Belmont, 1997.]3.3 Branch and Bound I
Solve the following problem using the Branch and Bound algorithm. max 2x1+ 3x2 x x1,x2?Z+?
Each LP subproblem may be solved graphically.
17ExercisesOperations Research L. Liberti
3.4 Branch and Bound II
Solve the following problem using the Branch and Bound algorithm. maxz?= 3x1+ 4x2 x1,x2≥0,intere
Each LP subproblem may be solved graphically.
3.5 Knapsack Branch and Bound
An investment bank has a total budget of 14 million euros, and can make 4 types of investments (numbered
1,2,3,4). The following tables specifies the amount to be invested and the net revenue for each investment.
Each investment must be made in full if made at all.Investment
1 2 3 4
Amount5 7 4 3
Net revenue
16 22 12 8
Formulate an integer linear program to maximize the total net revenue. Suggest away, beside the simplex
algorithm, to solve the continuous relaxation of the problem, and use it within a Branch-and-Bound algorithm to solve the problem. [E. Amaldi, Politecnico di Milano]Knapsack Branch and Bound18
quotesdbs_dbs7.pdfusesText_13[PDF] operations manager next step
[PDF] operations on languages in theory of computation
[PDF] operator number australia
[PDF] operator overloading in c++
[PDF] operator overloading in c++ ppt
[PDF] operators and expressions in c language
[PDF] operators and precedence in c
[PDF] opers plop
[PDF] opinie o sanatorium marysie?ka cieplice
[PDF] opinion words list
[PDF] opinion writing transition words 2nd grade
[PDF] opinion writing transition words anchor chart
[PDF] öpnv berlin app android
[PDF] opportunities for american airlines swot

