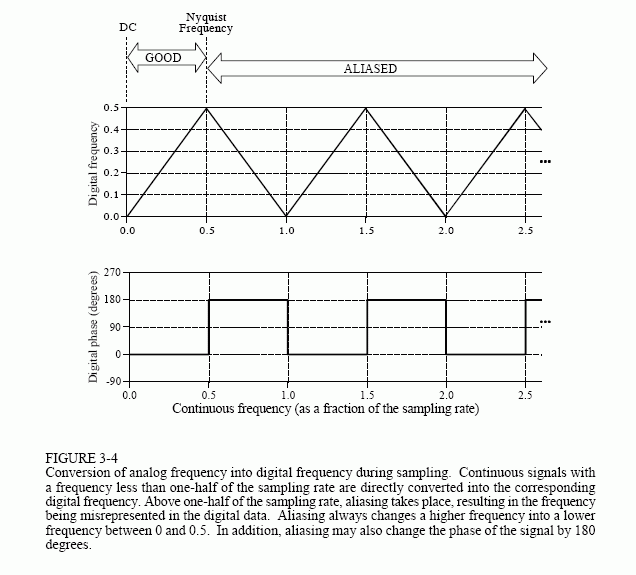
the roc of z transform of any signal cannot contain poles.
|
ECE 768 - Special Topics in Signal Processing: Models of the Neuron
1 oct. 2003 The z-transform of an arbitrary sequence x[n] is equivalent to ... Property 3: The ROC cannot contain any poles. |
|
Digital Signal Processing Properties of the z-Transform Region of
ROC Properties for Rational ?-Transforms (1 of 2). 1. The ROC is a ring or a disk in the z-plane centered at the origin. 2. The ROC cannot contain any poles |
|
The z-transform
Consider the signal x[n] = a the signal has a finite amplitude and that the z-transform is a rational function: ... The ROC cannot contain any poles. |
|
Chapter 4 The z - Transform
The z-Transform. D igital Signal Processing. Revise 20/10/2004. Page 13. Property 3 : The ROC cannot contain any poles. Property 4 : If x[n] is a finite- |
|
Untitled
signals. The z-transform is the discrete X is called an eigen-function of the system A ... X |
|
Transform Domain Representation of Discrete Time Signals The Z
2. The Fourier Transform of x[n] converges absolutely if and only if the ROC of the z- transform includes the unit circle. 3. ROC cannot contain any poles. |
|
Z Transform
24 janv. 2014 The Z-transform of a discrete time signal x(n) is ... z-Transform & ROC of finite duration sequence ... The ROC cannot contain any poles. |
|
Z Transform Rational Z-Transform
Shows the location of zeros by (o). Definition of ROC of a z-transform should not contain any poles. Determine the pole-zero plot for the signal. Im(z). |
|
The Z-Transform
Counterpart of the Laplace transform for discrete-time signals Fourier Transform does not exist for all signals ... The ROC cannot contain any poles. |
|
Chapter 2 The z-Transform
Intro. to Digital Signal Processing Review (with some extensions) the z-transform learned in the Signals ... (3) The ROC cannot contain any poles. |
|
Z Transform Questions and Answers - Sanfoundry
ROC 1 TheROCcannotcontainanypoles Ifdisapole thenX(d)= andthe z-transformdoesnotconvergeatthepole 2 TheROCforafinite-durationx[n]includestheentirez-plane except possiblyz=0orz= 2 n Forfinite-durationx[n]wemightsupposethat z x nz n1X(z)willconverge ifeachtermofx[n]isfinite |
|
Chapter 7: The z-Transform
•As the Laplace transform the ROC cannot contain any poles •ROC for a ?nite-duration signal includes the entire z-plane except possibly z = 0 or z = ?or both •Left-sided sequence:x[n] = 0 for n ?0 (notice the difference between the left-sided signal for Laplace transform) •Right-sided sequence:x[n] = 0 for n < 0 |
|
22 The z-Transform - MIT OpenCourseWare
The ROC does not contain poles The ROC of X(z) consists of a ring in the z-plane centered about the origin y7x[n][converges ROC includes the unitcircle in the z-plane x [n] finite duration => ROC is entire z-planewith the possibleexception of z = 0 or z = oo TRANSPARENCY 22 6 Properties of the ROCfor a right-sidedsequence N1 |
|
About the region of convergence of the z-transform
In general a sequence can be two-sided in that case the ROCof its z-transform is obviously the intersection of the ROC’s corresponding to its causal and anticausal parts We can summarize the results for the ROC of z-transforms as follows: The Region of Convergence of the z-transform of a sequence can have one of the following forms: |
Does the ROC of the Z-transform of any signal contain poles?
The ROC of z-transform of any signal cannot contain poles. Explanation: Since the value of z-transform tends to infinity, the ROC of the z-transform does not contain poles.
What is the ROC of a Z-transform?
The ROC for a given , is defined as the range of for which the z-transform converges. Since the z-transform is a power series, it converges when is absolutely summable. Stated differently, must be satisfied for convergence. The Region of Convergence has a number of properties that are dependent on the characteristics of the signal, .
What is the region of convergence of the Z-transforms(Z)?
for which the in?nite sum converges, such set of values of z is called the Region of Convergence of the z-transformS(z). This document describes the possible shapes the Region of Convergence (ROC) may take. We start by describing the ROC shape of one sided sequences from which we’ll deduce the ROC shape for two sided sequences.
What are the main topics of the Z-transform?
?Properties of the z-Transform ?Inversion of the z-Transform ?The Transfer Function ?Causality and Stability ?Determining Frequency Response from Poles & Zeros ?Computational Structures for DT-LTI Systems ?The Unilateral z-Transform 2
|
Two-sided - ECE 768 - Special Topics in Signal Processing: Models
1 oct 2003 · Property 2: The Fourier transform of x[n] converges absolutely iff the ROC of the z-transform of x[n] includes the unit circle Property 3: The ROC cannot contain any poles Property 4: If x[n] is a finite-duration sequence, then the ROC is the entire z-plane, except possibly z = 0 or z = ∞ |
|
The z-transform
The ROC cannot contain any poles If x[n] is finite duration (ie zero except on finite interval −∞ < N1 ≤ n ≤ N2 < ∞), then the ROC is the entire z-plane except perhaps at z = 0 or z = ∞ If x[n] is a right-sided sequence then the ROC extends outward from the outermost finite pole to infinity |
|
The z-transform and Analysis of LTI Systems - Eecs Umich
The z-transform of a signal is an infinite series for each possible value of z in the So we have two possible distinct definitions for the ROC: “the z values where There cannot be any poles in the ROC, so all the poles must be inside (or on |
|
The Z-Transform
Counterpart of the Laplace transform for discrete-time signals The z-Transform is often time more convenient to use The ROC cannot contain any poles |
|
Chapter 2 The z-Transform - NCTU - MAPL
Intro to Digital Signal Processing Fall 2011 Review (with some extensions) the z-transform learned in the Signals (3) The ROC cannot contain any poles |
|
Digital Signal Processing The z-transform - Indico
The Fourier transform of xŒnН converges absolutely if and only if the ROC of the z-transform includes the unit circle The ROC cannot contain any poles |
|
Chapter 10 THE z-TRANSFORM
The z-transform of a general discrete-time signal x[n] is defined as (10 3) Property 2: The ROC does not contain any poles Property 3: If x[n] is expressed as a ratio of polynomials in z, the order of the numerator cannot be greater than the |
|
Digital Signal Processing Properties of the z-Transform - spinlab
The ROC cannot contain any poles 3 If {x[n]} is a finite-length sequence, then the ROC is the entire z-plane |
|
Z Transform - CityU EE
the Fourier transform for discrete-time signals What are the pole(s) and zero(s) of X(z)? P3: The ROC cannot contain any poles (e g , Examples 5 1 to 5 5) |