relation binaire pdf

PDF

Binary Relations

Binary Relations Intuitively speaking: a binary relation over a set A is some relation R where for every x y ∈ A the statement xRy is either true or false Examples: < can be a binary relation over N Z R etc ↔ can be a binary relation over undirected graph G = (V E) V for any ≡k is a binary relation over Z for any integer k

PDF

Binary Relations

Binary Relations A binary relation over a set A is some relation R where for every x y ∈ A the statement xRy is either true or false Examples: < can be a binary relation over ℕ ℤ ℝ etc ↔ can be a binary relation over V for any undirected graph G = (V E) ≡ₖ is a binary relation over ℤ for any integer k

PDF

Binary Relations

Many relations can be chained together Examples: If x = y and y = z then x = z If R ⊆ S and S ⊆ T then R ⊆ T If x ≡ₖ y and y ≡ₖ z then x ≡ₖ z These relations are called transitive A binary relation R over a set A is called transitive if the following frst-order statement is true about R: ∀a ∈ A ∀b ∈ A ∀c ∈ A

PDF	Contribution Relations binaires dans un ensemble à 3 éléments Une relation binaire R d'un ensemble E vers un ensemble F est définie comme un ensemble de couples (x; y) ∈ E × F c'est-à-dire un sous-ensemble du produit

PDF	RELATION BINAIRE La relation binaire est une relation d'équivalence si vous n'êtes pas convaincu : donc est réflexive Si alors ( étant vraie pour tout et pour tout ) Donc

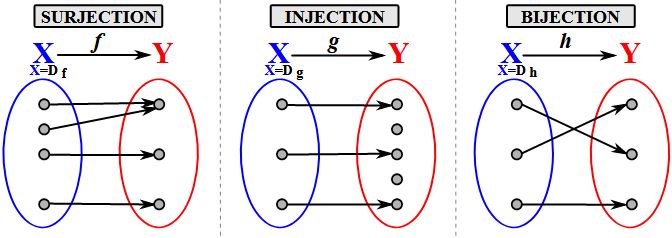
PDF	Relations Definition (irreflexive relation): A relation R on a set A is called irreflexive if (aa) R for every a A Example 1: • Assume relation R≠on A={1234} such that a R≠b if and only if a ≠b • Is R≠irreflexive? • R≠={(12)(13)(14)(21)(23)(24)(31)(32)(34)(41)(42)(43)} • Answer: Yes

C'est quoi un couple binaire ?
Autrement dit une relation binaire est une collection de couples, ( x , y ) (x, y) (x,y) tel que : x ∈ E x \\in E x∈E: la première composante du couple est dans E E E. y ∈ F y \\in F y∈F : la seconde dans F F F.
Quand Dit-on qu'une relation est réflexive ?
Une relation R est réflexive si pour tout x ∈ E on a xRx.
Diagramme cartésien : la diagonale doit être notée.
Diagramme sagittal : chaque sommet admet une boucle.
Exemples : Quel que soit l'ensemble, la relation d'égalité = est réflexive.
Comment montrer la relation d'équivalence ?
Une relation binaire est une relation d'équivalence si et seulement si elle est réflexive, symétrique et transitive. deux ensembles, et f une application de E dans F.
La relation sur E définie par aRb ⇔ f(a) = f(b) est une relation d'équivalence.
Certaines relations d'ordre sont des relations totales, c'est-à-dire que deux éléments de E sont toujours comparables : pour tous x, y de E : x ≤ y ou y ≤ x.
On dit alors que ≤ est une relation d'ordre total, et que l'ensemble E est totalement ordonné par cette relation.

Exercice 1 :

Soit { } et la relation binaire sur dont le graphe est {( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )} Vérifier que la relation est une relation d’équivalence. Faire la liste des classes d’équivalences distinctes et donner l’ensemble quotient . Allez à : Correction exercice 1 : licence-math.univ-lyon1.fr

Exercice 3 :

Sur , on considère la relation définie par ( ) ( ) Montrer que est une relation d’équivalence. Décrire la classe d’équivalence ( ̇ ) du couple ( ). On désigne par l’ensemble quotient pour cette relation. Montrer que l’application ( ̇ ) Est bien définie et que c’est une bijection. Allez à : Correction exercice 3 : [ [ licence-math.univ-lyon1.fr

Exercice 4 :

Soient et deux ensembles et ( ) , une application. On définit une relation sur en posant, pour tout ( ) ( ) Montrer que est une relation d’équivalence. Décrire la classe de l’élément . Pourquoi l’application ̇ ( ) Est-elle bien définie ? Montrer qu’elle est injective. Que peut-on conclure sur l’ensemble quotient ? Allez à

Exercice 5 :

Soit un ensemble et soit une partie de . On définit dans posant, pour tout couple ( ) de parties de : ( ) la relation d’équivalence en Expliciter les classes ̇, ̇, et ̇. Montrer que si , alors est l’unique représentant de Expliciter une bijection entre ( ) et ( ). contenu dans . Remarque : ne pas hésiter, si nécessaire, à

Exercice 8 :

Dans , on définit une relation en posant Montrer que est une relation d’ordre partiel sur . On considère dans la suite de l’exercice que l’ensemble est ordonné par la relation . L’ensemble possède-t-il un plus grand élément ? un plus petit élément ? Soit { }. L’ensemble possède-t-il un plus grand élément ? Un plus petit élément ?

Exercice 14 :

Les relations défines ci-dessous sont-elles des relations d’équivalence sur ? licence-math.univ-lyon1.fr

Correction exercice 3 :

1. ( ) ( ) est réflexive. ( ) ( ) est symétrique. ( ) ( ) { ( ) ( ) { , autrement [ ]. Il y a ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’équivalence. 2. ( ) ( ) ( ) ( ) Si on pose alors , donc la classe de ( ) est le cercle de centre ( ) de rayon . Si ( ) ( ) la classe de ( ) est réduite

Correction exercice 4 :

( ) ( ) est réflexive. ( ) ( ) ( ) ( ) est symétrique. ( ) ( ) { { ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’équivalence. Pour tout ̇, et donc ( ) ( ) donc ̇ { ( ) ( )} Notons cette « application », c’est le même problème que dans l’exercice précédent, pour une classe on doit le même résultat qu

Correction exercice 6 :

Pour tout est réflexive. est symétrique. Cherchons un peu { { Il faudrait pouvoir en déduire que et à ce moment là on doit se dire que cela n’a pas l’air évident et que donc, puisque l’énoncé demande « la relation est-elle transitive ? » et non pas « montrer que la relation est transitive » il se peut que la réponse soit « non », on va donc c

Si {

alors il existe tels que { , d’où , en simplifiant par , . et sont deux entiers positifs, la seul solution est est antisymétrique. , on en déduit que . Si { alors il existe tels que { , d’où , comme on a . est transitive. Finalement est une relation d’ordre partiel. Remarque : n’est pas une relation d

Correction exercice 9 :

1. Pour tout Il existe tel que donc . est réflexive. S’il existe tels que { alors ( ) entiers positifs, la seule solution est est antisymétrique. , par conséquent donc . , comme et sont des Si { il existe tels que { est une relation d’ordre partiel. Remarque : alors ( ) comme on a . Ce n’est pas une relation d’ordre totale

Correction exercice 10 :

1. ( ) donc ( ) ( ). est réflexive. ( ) ( ) { ( ) ( ) { ( ( ) ) { { { { { ( ) ( ) est antisymétrique. ( ) ( ) { ( ) ( ) { ( ( ) ) { { { { ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’ordre (partiel). Est-ce que cette relation est

Correction exercice 16 :

Première méthode donc , est réflexive. Si et alors et donc car ( ) et entraine ( ) ( ) ( ) ( )( ) en particulier . Donc est antisymétrique. Si et alors et donc , d’où . est transitive. Finalement est une relation d’ordre. Soit et alors , soit et alors , il s’agit d’une relation d’ordre total. Deuxième

Si ( ) ( ) et

est réflexive. ( ) ( ) alors ( ) ( ) donc est symétrique. { alors { car Donc , on multiplie par et on simplifie par , on a alors , c’est-à-dire ( ) ( ), donc est transitive. est une relation d’équivalence. licence-math.univ-lyon1.fr

Correction exercice 20 :

{ { donc { d’où ( ) ( ), est réflexive. ( ) ( ) ( { ( ) ( ) { ( ) ) { { { { { { ( ) ( ) est antisymétrique. licence-math.univ-lyon1.fr

Correction exercice 21 :

( ) ( ) a zéro élément. Donc on a . est réflexive. Si , ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments. Alors ( ) ( ) ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments. Donc est réflexive. Si et alors ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments et ( ) ( ) est un ensemble fini

Exercice 1 :

Exercice 3 :

Exercice 4 :

Exercice 5 :

Exercice 8 :

Exercice 14 :

Les relations défines ci-dessous sont-elles des relations d’équivalence sur ? licence-math.univ-lyon1.fr

Correction exercice 3 :

Correction exercice 4 :

Correction exercice 6 :

Si {

Correction exercice 9 :

Correction exercice 10 :

Correction exercice 16 :

Si ( ) ( ) et

Correction exercice 20 :

{ { donc { d’où ( ) ( ), est réflexive. ( ) ( ) ( { ( ) ( ) { ( ) ) { { { { { { ( ) ( ) est antisymétrique. licence-math.univ-lyon1.fr

Correction exercice 21 :

PDF	1. Relations binaires 2. Relations déquivalence 3. Relations dordre C5 : Relations. 1. Relations binaires. Définition. Une relation binaire R sur un ensemble E est une propriété portant sur les couples.

PDF	Chapitre 4 - Relations binaires sur un ensemble. Une relation binaire R sur un ensemble E qui est réflexive transitive et antisymétrique est appelée relation d'ordre sur E. La plupart des relations d'ordre

PDF	RELATION BINAIRE Relation binaire. Pascal Lainé. 3. Exercice 11 : Soient un ensemble fini non vide et un élément fixé de . Les relations définies ci-dessous sont-elles des.

PDF	RELATIONS BINAIRES Définition (Propriétés des relations binaires) Soit une relation binaire sur E. • Réflexivité : On dit que est réflexive si : ?x ? E x x. • Transitivité

PDF	Relations binaires. Relations déquivalence et dordre 20 Aug 2017 Définition 1 : Une relation binaire ? définie sur un ensemble E est au choix : • une propriété qui relie ou non deux éléments x et y de E.

PDF	1 Mathématiques pour lInformatique Relations binaires Jérôme Relations binaires. Jérôme Gensel. I) Relations binaires. 1. Généralités. Définition 1 : Une relation binaire d'un ensemble E vers un ensemble F est une

PDF	Relation Une relation binaire R d'un ensemble de départ E vers un ensemble d'arrivée F est définie par une partie GR ? E × F. Si (xy) ? GR

PDF	Table des mati`eres Les relations binaires sont classées en fonction de leur propriétés. Définition 1.1.2 Une relation binaire R sur E est dite. - réflexive si ?a ? E a R a

PDF	Relations-binaires.pdf Relations d'équivalence. Exercice 1 [ 02643 ] [Correction]. Soit R une relation binaire sur un ensemble E à la fois réflexive et transitive.

PDF	Decomposition rectangulaire optimale dune relation binaire Mots-des: Strategie de decomposition rectan^aire relation binaire

PDF	1 Relations binaires 2 Relations déquivalence 3 Relations dordre Une relation binaire est une relation d'équivalence si et seulement si elle est réflexive symétrique et transitive Exemples Le parallélisme est une relation

PDF	Relations binaires sur un ensemble De façon informelle une relation binaire sur un ensemble E est une proposition qui lie entre eux certains éléments de cet ensemble

PDF	RELATION BINAIRE - Licence de mathématiques Lyon 1 Relation binaire Pascal Lainé 1 RELATION BINAIRE Exercice 1 : Soit { } et la relation binaire sur dont le graphe est {( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )}

PDF	RELATIONS BINAIRES - Christophe Bertault Christophe Bertault — Mathématiques en MPSI RELATIONS BINAIRES Dans tout ce chapitre E est un ensemble quelconque 1 RELATIONS BINAIRES SUR UN ENSEMBLE

PDF	Relations binaires Relations déquivalence et dordre 20 août 2017 · Définition 1 : Une relation binaire ? définie sur un ensemble E est au choix : • une propriété qui relie ou non deux éléments x et y de E

PDF	Relations binaires - Xiffr On définit une relation binaire R sur G par : xRy ?? xy?1 ? H Montrer que R est une relation d'équivalence et en décrire les

PDF	Relation - Université de Toulouse Définition Relation binaire Une relation binaire R d'un ensemble de départ E vers un ensemble d'arrivée F est définie par une partie GR ? E × F

PDF	Relations binaires sur un ensemble Définition et exemples de relation binaires sur un ensemble 0 1 1 Définitions 1 Sur tout ensemble E l'égalité = sur E est une relation binaire

PDF	Relations binaires sur E Relations d´equivalence Relations dordre Relations d'ordre 1 Relations binaires de E dans E : représentations propriétés 1 Exercice corrigé en amphi ? est une relation binaire sur un ensemble

PDF	1 Cours 3: Relations binaires sur un ensemble Cours 3: Relations binaires sur un ensemble 1 1 Notion de relation: On appelle relation dVun ensemble A vers un ensemble B toute correpondance * qui lie

Qu'est-ce qu'un couple binaire ?
En mathématiques, une relation binaire entre deux ensembles E et F (ou simplement relation entre E et F) est définie par un sous-ensemble du produit cartésien E × F, soit une collection de couples dont la première composante est dans E et la seconde dans F. Cette collection est désignée par le graphe de la relation.
Comment montrer qu'une relation est une relation d'équivalence ?
Une relation R sur un ensemble E est une relation d'équivalence sur E si elle vérifie ces trois propriété :
Réflexivité : Pour tout de x de E, xRx.Symétrie : Pour tout (x,y) de E, si xRy alors yRx.Transitivité : Pour tout (x,y,z) de E si xRy et yRz alors xRz.
Quand Dit-on qu'une relation est symétrique ?
Une relation R est symétrique si pour tout x,y ? E on a xRy si et seulement si yRx. Diagramme cartésien : symétrie par rapport à la diagonale. Diagramme sagittal : quand une fl?he va de a vers b, il y a aussi une fl?he de b vers a. Exemples : Quel que soit l'ensemble, la relation d'égalité = est symétrique.
Plus formellement, une relation ? est dite antisymétrique si elle vérifie la condition suivante : (x ? y ? y ? x) ? x = y. En d'autres termes, si, dans une relation ? on a à la fois le couple (x, y) et son couple réciproque (y, x), alors x et y sont un seul et même élément.

Share on Facebook Share on Whatsapp

Choose PDF

More..

PDF	Binary Relations - Stanford University

PDF	1 Relations binaires - Côte d'Azur University

PDF	Christophe Bertault — Mathématiques en MPSI RELATIONS BINAIRES

PDF	1 Relations binaires - unicefr

PDF	DECIMAL BINARY AND HEXADECIMAL - University of Washington

PDF	Searches related to relation binaire pdf filetype:pdf

Quelle est la différence entre une relation binaire et une relation d'équivalence?

Une relation binaire est une relation d'équivalence si et seulement si elle est ré\u001Dexive, symétrique et transitive.
. Exemples.
. Le parallélisme est une relation d'équivalence sur l'ensemble des droites.
. Soit E et F deux ensembles, et f une application de E dans F.
. La relation sur E dé\u001Cnie par aRb ,f(a) = f(b) est une relation d'équivalence.

Quelle est la différence entre une relation binaire et un parallélisme?

Une relation binaire est une relation d'équivalence si et seulement si elle est ré\u001Dexive, symétrique et transitive.
. Exemples.
. Le parallélisme est une relation d'équivalence sur l'ensemble des droites.

Comment calculer une relation d'équivalence?

Soit E et F deux ensembles, et f une application de E dans F.
. La relation sur E dé\u001Cnie par aRb ,f(a) = f(b) est une relation d'équivalence.
. Définition.
. Soit Rune relation d'équivalence sur E, et a un élément de E.

PDF	Relations binaires sur un ensemble Plus proprement, une relation binaire R sur un ensemble E est définie par une partie G de E × E Si (x, y) ∈ G on dit que x est en relation avec y et on le note ” xRy”

PDF	1 Relations binaires 2 Relations déquivalence 3 Relations dordre C5 : Relations 1 Relations binaires Définition Une relation binaire R sur un ensemble E est une propriété portant sur les couples d'éléments de E On notera

PDF	RELATIONS BINAIRES - Christophe Bertault Définition (Relation binaire sur un ensemble) On appelle relation binaire sur E toute Exemple Vous connaissez depuis toujours certaines relations binaires :

PDF	RELATION BINAIRE - Licence de mathématiques Lyon 1 Relation binaire Pascal Lainé 3 Exercice 11 : Soient un ensemble fini non vide et un élément fixé de Les relations définies ci-dessous sont-elles des relations

PDF	Relation - Université de Toulouse Une relation binaire R d'un ensemble de départ E vers un ensemble d'arrivée F est définie par une partie GR ⊆ E × F Si (x,y) ∈ GR, on dit que x est en relation

PDF	Relations binaires - MPSI Corot Relations binaires 1 Généralités Définition 1 1 Relation binaire On appelle relation binaire sur un ensemble E toute partie ℛ de E2 Pour ( , ) ∈ E2, la

PDF	Relations binaires Relations déquivalence et d - Lycée dAdultes 20 août 2017 · Définition 1 : Une relation binaire 勿 définie sur un ensemble E est au choix : • une propriété qui relie ou non deux éléments x et y de E On note

PDF	Relations binaires sur un ensemble 0 1 2 Exemples 1 Sur tout ensemble E l'égalité = sur E est une relation binaire Son graphe est Γ= = ∆E = {(

PDF	1 Mathématiques pour lInformatique Relations binaires Jérôme Définition 1 : Une relation binaire d'un ensemble E vers un ensemble F est une partie R de E×F Si (x,y)∈R on dit que x est en relation avec y et on note xRy

PDF	Chapitre 3 :Relations dordre Dans tout ce qui suit, E désigne un ensemble quelconque I Généralités A) Relations binaires Une relation binaire définie sur E est une propriété que chaque