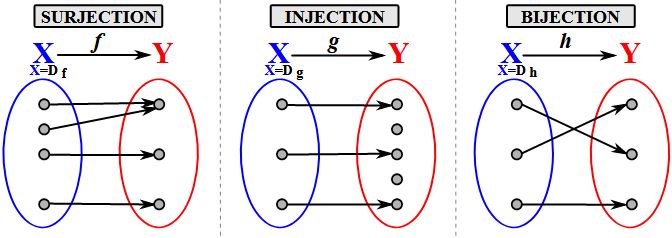
exercice relation d'equivalence
|
1 Exemples simples de relations d’équivalence
x f y ssi f(x) = f(y): Prouvez que est une relation d’équivalence Exercice 6 Soit E = fa; b; c; dg et la relation sur E dont l’ensemble suivant donne la liste de tous les couples (x; y) tels que x y : G = f(a; a); (a; b); (a; c); (b; b); (b; a); (c; c); (c; a); (c; b); (d; d)g: 1 |
|
Relation d’équivalence relation d’ordre 1 Relation d’équivalence
Exercice 1 Dans C on définit la relation par : z z0 jzj = jz0j: R Montrer que est une relation d’équivalence R Déterminer la classe d’équivalence de chaque z 2 C Exo7 Indication Corection Vidéo Exercice 2 Montrer que la relation définie sur R par : R [0209] est une relation d’équivalence Préciser pour y () xey = yex R |
|
TD2 : Relations d’ordre et d’équivalence (avec corrigé)
Exercice 1: Prouvez que la relation sur Z aRb ⇔ a − b est un multiple de 5 est une relation d’équivalence Solution: On vérifie les 3 conditions : — Réflexivité : Soit x ∈ Z On veut prouver xRx c’est à dire x− est un multiple de 5 On a x − x = 0 = 5 × 0 Par conséquent x − x est un multiple de 5 donc xRx — Symétrie : Soit x y ∈ Z |
|
Worksheet on Relations and Equivalence Relations and Classes
In symbols [a] = fb 2 A : (a; b) 2 Rg: For each equivalence relation list the equivalence classes The relation = on the integers The relation has the same size on the power set of fa; bg The relation on A = f1; 2; 3; 4g given by = f(1; 1); (2; 2); (3; 3); (4; 4); (1; 2); (2; 1)g: The relation on Z de ned by |
Comment définir une relation d’équivalence ?
Montrer que est une relation d’équivalence. est une relation d’équivalence. Préciser, pour [0212] . Soit (E;6) un ensemble ordonné. On définit sur (E) n f/0g la relation Vérifier que c’est une relation d’ordre. Un dessin permettra d’avoir une bonne idée de ce qui se passe... Pour la transitivité on pourra calculer xyez.
Comment calculer une relation d’ordre et d’équivalence ?
TD2 : Relations d’ordre et d’équivalence (avec corrigé) est une relation d’équivalence. Solution: On vérifie les 3 conditions : — Réflexivité : Soit x ∈ Z. On veut prouver xRx, c’est à dire x− est un multiple de 5.On a x − x = 0 = 5 × 0. Par conséquent, x − x est un multiple de 5, donc xRx. — Symétrie : Soit x, y ∈ Z.
Comment calculer l'équivalence d'une relation ?
Montrer que est une relation d'équivalence. Déterminer la classe d'équivalence de pour tout réel . Déterminer l'ensemble quotient. Montrer que est une relation d’ordre total. Allez à : Correction exercice 16 : 1. Soit Soit , déterminer en fonction de l’ensemble des complexes tels que . 2.
Comment trouver la classe d'équivalence d'une relation ?
1. Trouvez une application f : R ! R telle que la relation soit de la forme f. 2. Déterminer [1], la classe d’équivalence de 1, et [ 1], la classe d’équivalence de 1. 3. Trouvez tous les x 2 R dont la classe d’équivalence est un ensemble qui ne contient qu’un seul élément.
Exercice 1 :
Soit { } et la relation binaire sur dont le graphe est {( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )} Vérifier que la relation est une relation d’équivalence. Faire la liste des classes d’équivalences distinctes et donner l’ensemble quotient . Allez à : Correction exercice 1 : licence-math.univ-lyon1.fr
Exercice 3 :
Sur , on considère la relation définie par ( ) ( ) Montrer que est une relation d’équivalence. Décrire la classe d’équivalence ( ̇ ) du couple ( ). On désigne par l’ensemble quotient pour cette relation. Montrer que l’application ( ̇ ) Est bien définie et que c’est une bijection. Allez à : Correction exercice 3 : [ [ licence-math.univ-lyon1.fr
Exercice 4 :
Soient et deux ensembles et ( ) , une application. On définit une relation sur en posant, pour tout ( ) ( ) Montrer que est une relation d’équivalence. Décrire la classe de l’élément . Pourquoi l’application ̇ ( ) Est-elle bien définie ? Montrer qu’elle est injective. Que peut-on conclure sur l’ensemble quotient ? Allez à
Exercice 5 :
Soit un ensemble et soit une partie de . On définit dans posant, pour tout couple ( ) de parties de : ( ) la relation d’équivalence en Expliciter les classes ̇, ̇, et ̇. Montrer que si , alors est l’unique représentant de Expliciter une bijection entre ( ) et ( ). contenu dans . Remarque : ne pas hésiter, si nécessaire, à
Exercice 8 :
Dans , on définit une relation en posant Montrer que est une relation d’ordre partiel sur . On considère dans la suite de l’exercice que l’ensemble est ordonné par la relation . L’ensemble possède-t-il un plus grand élément ? un plus petit élément ? Soit { }. L’ensemble possède-t-il un plus grand élément ? Un plus petit élément ?
Exercice 14 :
Les relations défines ci-dessous sont-elles des relations d’équivalence sur ? licence-math.univ-lyon1.fr
Correction exercice 3 :
1. ( ) ( ) est réflexive. ( ) ( ) est symétrique. ( ) ( ) { ( ) ( ) { , autrement [ ]. Il y a ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’équivalence. 2. ( ) ( ) ( ) ( ) Si on pose alors , donc la classe de ( ) est le cercle de centre ( ) de rayon . Si ( ) ( ) la classe de ( ) est réduite
Correction exercice 4 :
( ) ( ) est réflexive. ( ) ( ) ( ) ( ) est symétrique. ( ) ( ) { { ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’équivalence. Pour tout ̇, et donc ( ) ( ) donc ̇ { ( ) ( )} Notons cette « application », c’est le même problème que dans l’exercice précédent, pour une classe on doit le même résultat qu
Correction exercice 6 :
Pour tout est réflexive. est symétrique. Cherchons un peu { { Il faudrait pouvoir en déduire que et à ce moment là on doit se dire que cela n’a pas l’air évident et que donc, puisque l’énoncé demande « la relation est-elle transitive ? » et non pas « montrer que la relation est transitive » il se peut que la réponse soit « non », on va donc c
Si {
alors il existe tels que { , d’où , en simplifiant par , . et sont deux entiers positifs, la seul solution est est antisymétrique. , on en déduit que . Si { alors il existe tels que { , d’où , comme on a . est transitive. Finalement est une relation d’ordre partiel. Remarque : n’est pas une relation d
Correction exercice 9 :
1. Pour tout Il existe tel que donc . est réflexive. S’il existe tels que { alors ( ) entiers positifs, la seule solution est est antisymétrique. , par conséquent donc . , comme et sont des Si { il existe tels que { est une relation d’ordre partiel. Remarque : alors ( ) comme on a . Ce n’est pas une relation d’ordre totale
Correction exercice 10 :
1. ( ) donc ( ) ( ). est réflexive. ( ) ( ) { ( ) ( ) { ( ( ) ) { { { { { ( ) ( ) est antisymétrique. ( ) ( ) { ( ) ( ) { ( ( ) ) { { { { ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) est transitive. Finalement est une relation d’ordre (partiel). Est-ce que cette relation est
Correction exercice 16 :
Première méthode donc , est réflexive. Si et alors et donc car ( ) et entraine ( ) ( ) ( ) ( )( ) en particulier . Donc est antisymétrique. Si et alors et donc , d’où . est transitive. Finalement est une relation d’ordre. Soit et alors , soit et alors , il s’agit d’une relation d’ordre total. Deuxième
Si ( ) ( ) et
est réflexive. ( ) ( ) alors ( ) ( ) donc est symétrique. { alors { car Donc , on multiplie par et on simplifie par , on a alors , c’est-à-dire ( ) ( ), donc est transitive. est une relation d’équivalence. licence-math.univ-lyon1.fr
Correction exercice 20 :
{ { donc { d’où ( ) ( ), est réflexive. ( ) ( ) ( { ( ) ( ) { ( ) ) { { { { { { ( ) ( ) est antisymétrique. licence-math.univ-lyon1.fr
Correction exercice 21 :
( ) ( ) a zéro élément. Donc on a . est réflexive. Si , ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments. Alors ( ) ( ) ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments. Donc est réflexive. Si et alors ( ) ( ) est un ensemble fini qui a un nombre pair d’éléments et ( ) ( ) est un ensemble fini
![Exercice 2 (Relation déquivalence relation dordre) [00212] Exercice 2 (Relation déquivalence relation dordre) [00212]](https://pdfprof.com/FR-Documents-PDF/Bigimages/OVP.08M3UmLHd2TI6rr_horhLgEsDh/image.png)
Exercice 2 (Relation déquivalence relation dordre) [00212]
![Exercice 1 (Relation déquivalence relation dordre) [00209] Exercice 1 (Relation déquivalence relation dordre) [00209]](https://pdfprof.com/FR-Documents-PDF/Bigimages/OVP.1GQDS8y-NS2V2Ey2q9EEiwEsDh/image.png)
Exercice 1 (Relation déquivalence relation dordre) [00209]

TD N° 2 Algebre 1: exercice 7 et 8. Relation déquivalence et classe déquivalence
|
RELATION BINAIRE
Exercice 5 : Soit un ensemble et soit une partie de . On définit dans ( ) la relation d'équivalence en posant pour tout couple ( ) |
|
Relations déquivalence Exercice 1. ? “) Exercice 2. ? “) Exercice 3. ?
25 Sept 2018 Montrer que R est une relation d'équivalence. Donner la classe d'équivalence de (1; 2). Exercice 11. ? “. Sur R. |
|
Relation déquivalence relation dordre
et après une étude de fonction on calculera le nombre d'antécédents possibles. 2. Page 3. Correction de l'exercice 1 ?. 1. Soient |
|
1 Exemples simples de relations déquivalence 2 Construction de
autre relation (d'équivalence ou non). Les exercices de cette section proposent plusieurs situations de ce type. Exercice 5. Soit E et F deux ensembles |
|
TD no 7 — Relations déquivalence
Étant donné un réel x calculer sa classe d'équivalence. Combien y a-t-il d'éléments dans cette classe ? Exercice 3. On définit une relation ? sur P( |
|
Corrigé du TD no 7
Il est facile de vérifier que cette application est bijective d'où le résultat. 2. Page 3. Exercice 5. On considère la relation R sur Z × Z? |
|
Arithmétique FICHE I: Relations déquivalence Exercice 1. Trouver
(2) Lister les classes d'équivalence et donner l'ensemble quotient E/R. Exercice 3. On considère la relation d'équivalence sur R2 définie par. |
|
Exercices de mathématiques - Exo7
Exercice 129 Relation d'équivalence quotient. Soient R et S deux relations d'équivalence sur un ensemble E telles que : ? x |
|
TD 2 : Relations dordre et déquivalence
Exercice 3 : On pose I = [0; 2[ et on munit I de la relation d'ordre ?. 1. Est-ce que I admet un majorant ? une borne supérieure ? un plus grand élément ? 2. |
|
Séance du 09/02/2013 du club de maths dOrsay Relations d
9 Feb 2013 Exercice 2. Parmi ces relations binaires dire lesquelles sont des relations d'équivalence : La relation d'ordre ? sur R. La relation = sur ... |
|
Exercices corrigés -Relations déquivalence et relations dordre
Exercices corrigés - Relations d'équivalence et relations d'ordre · La relation n'est pas réflexive : une droite n'est pas orthogonale à elle-même · La relation |
|
RELATION BINAIRE - Licence de mathématiques Lyon 1
Exercice 2 : 1 Montrer que la relation de congruence modulo [ ] Est une relation d'équivalence sur 2 En vous servant de la division euclidienne |
|
Corrigé du TD no 7
Exercice 1 Dire si chacune des relations ci-dessous est réflexive symétrique ou transitive 1 La relation R sur Q définie par : xRy ? xy = 0 |
|
Relations déquivalence - Thierry Sageaux
25 sept 2018 · Exercice 14 Soient E et F deux ensembles et f ? FE Soit R la relation définie sur E par xRy |
|
Relations binaires - Xiffr
Montrer que S est une relation d'équivalence et que R permet de définir une relation d'ordre sur les classes d'équivalences de S Exercice 5 [ 02985 ] [ |
|
Exo7 - Exercices de mathématiques
Exercice 1 Dans C on définit la relation R par : zRz ? z = z 1 Montrer que R est une relation d'équivalence 2 Déterminer la classe d'équivalence de |
|
1 Relations binaires 2 Relations déquivalence 3 Relations dordre
Une relation binaire est une relation d'équivalence si et seulement si elle est réflexive symétrique et transitive Exemples Le parallélisme est une relation |
|
Relation déquivalence Relation dordre
Exercice 1 1 Soit E = N × N on définit R par : (a b)R(a b ) ? a + b = b + a Montrer que R est une relation d'équivalence Identifier E/R |
|
Relations binaires sur E Relations d´equivalence Relations dordre
Exercice corrigé en amphi Soit ? la relation binaire définie sur l'ensemble des entiers relatifs par : a?b si et seulement si a - b est pair (a) Montrer que |
|
1 Exemples simples de relations déquivalence 2 Construction de
Exercice 5 Soit E et F deux ensembles et f : E ? F une application On définit le relation ?f sur E comme suit : x ?f y ssi f(x) = f(y) |
Comment déterminer une relation d'équivalence ?
Une relation binaire est une relation d'équivalence si et seulement si elle est réflexive, symétrique et transitive. deux ensembles, et f une application de E dans F. La relation sur E définie par aRb ? f(a) = f(b) est une relation d'équivalence.Comment montrer qu'une relation est une relation d'équivalence ?
Une relation R sur un ensemble E est une relation d'équivalence sur E si elle vérifie ces trois propriété :
Réflexivité : Pour tout de x de E, xRx.Symétrie : Pour tout (x,y) de E, si xRy alors yRx.Transitivité : Pour tout (x,y,z) de E si xRy et yRz alors xRz.Quelle est la relation d'équivalence ?
Définition formelle
Une relation d'équivalence sur un ensemble E est une relation binaire ~ sur E qui est à la fois réflexive, symétrique et transitive. Plus explicitement : ~ est une relation binaire sur E : un couple (x, y) d'éléments de E appartient au graphe de cette relation si et seulement si x ~ y.- Plus formellement, une relation ? est dite antisymétrique si elle vérifie la condition suivante : (x ? y ? y ? x) ? x = y. En d'autres termes, si, dans une relation ? on a à la fois le couple (x, y) et son couple réciproque (y, x), alors x et y sont un seul et même élément.
| Relation d’équivalence |
| TD2 : Relations d’ordre et d’équivalence (avec corrigé) |
| Relation d’équivalence relation d’ordre 1 Relation d’équivalence |
| Fiche d’exercices n 7 : relations d’ equivalence - CNRS |
| 1 Exemples simples de relations d’équivalence - univ-amufr |
| Searches related to exercice relation d+equivalence filetype:pdf |
Comment calculer la relation d’équivalence ?
- e f
.Doncaf =be donc(a,b)R(e, f).
. Donc R est une relation d’équivalence. (b) Soit (a,b)?R?×R?.
Comment calculer les relations d’ordre et d’équivalence ?
- TD2 : Relations d’ordre et d’équivalence (avec corrigé) Exercice 1: (a) Prouvez que la relation surZ aRb ? a ?b est un multiple de 5 est une relation d’équivalence.
. Solution:On véri?e les 3 conditions : — Ré?exivité : Soit x ?Z.
. On veut prouver xRx, c’est à dire x? est un multiple de 5
.On a x ? x = 0 = 5 ×0.
Comment calculer la classe d’équivalence ?
- La classe d’équivalence de (a,b)est donc ˆ\u0010 x,xb a x ?R? Exercice 4: (a) Prouver que la relation surR aRb ? a =b est une relation d’équivalence.
. Solution: — Ré?exivité : Soit x ?R.
. Prouvons que xRx.
Comment savoir si un multiple de 5 est une relation d’équivalence ?
- aRb ? a ?b est un multiple de 5 est une relation d’équivalence.
. Solution:On véri?e les 3 conditions : — Ré?exivité : Soit x ?Z.
. On veut prouver xRx, c’est à dire x? est un multiple de 5
.On a x ? x = 0 = 5 ×0.
. Par conséquent, x ? x est un multiple de 5, donc xRx. — Symétrie : Soit x,y ?Z.
. On suppose xRy (ie. x ?y est un multiple de 5).
|
RELATION BINAIRE - Licence de mathématiques Lyon 1
Exercice 9 : Dans , on définit une relation en posant pour tout ( ) : 1 Montrer que est une relation d'ordre partiel |
|
Corrigé du TD no 7
Exercice 1 Dire si chacune des relations ci-dessous est réflexive, symétrique, Soit x ∈ R Par définition, la classe d'équivalence de x, notée Cl(x), est l' |
|
Relations déquivalence, classes déquivalence, ensemble quotient
Les exercices de cette section proposent plusieurs situations de ce type Exercice 5 Soit E et F deux ensembles, et f : E → F une application On définit le relation |
|
Relation déquivalence, relation dordre 1 Relation déquivalence 2
Déterminer la classe d'équivalence de z ∈ C Exercice 2 Soit R une relation binaire sur un ensemble E, symétrique et transitive Que penser du raisonnement |
|
Relations déquivalence Exercice 1 ˇ “) Exercice 2 ˇ “) Exercice 3 ˇ
25 sept 2018 · 3) Montrer que R est une relation d'équivalence 4) Préciser, pour x ∈ R, le nombre d'éléments dans x, classe de x modulo R Exercice 9 |
|
Arithmétique FICHE I : Relations déquivalence Exercice 1 Trouver
Exercice 1 Trouver toutes les relations d'équivalence possibles sur l'ensemble { 1,2,3} Exercice 2 Soit E = {1,2,3,4,5} et R la relation binaire donnée par |
|
Relation déquivalence Relation dordre - PAGE WEB DANDRE
Déterminer la classe d'équivalence de z ∈ C Exercice 4 Soit R une relation binaire sur un ensemble E, symétrique et transitive Que penser du raisonnement |
|
Algèbre Relations déquivalence
Relations d'équivalence Denis Vekemans ∗ Exercice 1 Soit E un ensemble et R une relation de E dans E Dans chacun des exemples ci-dessous, donner les |
|
Relations binaires - Université de Rennes 1
Exercice n◦3 Soient E un ensemble et A ∈ P(E) ; on définit sur P(E) la relation R par XRY si X ∩ A = Y ∩ A Montrer que c'est une relation d'équivalence |
|
Feuille 3 - Relations binaires sur E Relations d´equivalence
1 Exercice corrigé en amphi 고 est une relation binaire sur un ensemble E Ecrire ce que signifie : (a) 고 n'est |





![relation d'ordre) [00212 </b></h3></figcaption>
</figure>
<figure>
<img
data-src= PDF] Exercices corriges sur la finance mathematique](https://www.cours-gratuit.com/images/remos_downloads/detail2/id-8718.8717.pdf-full.jpg)