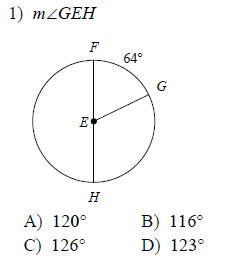
homework 2 central angles and arc measures
|
11-Arcs and Central Angles.pdf
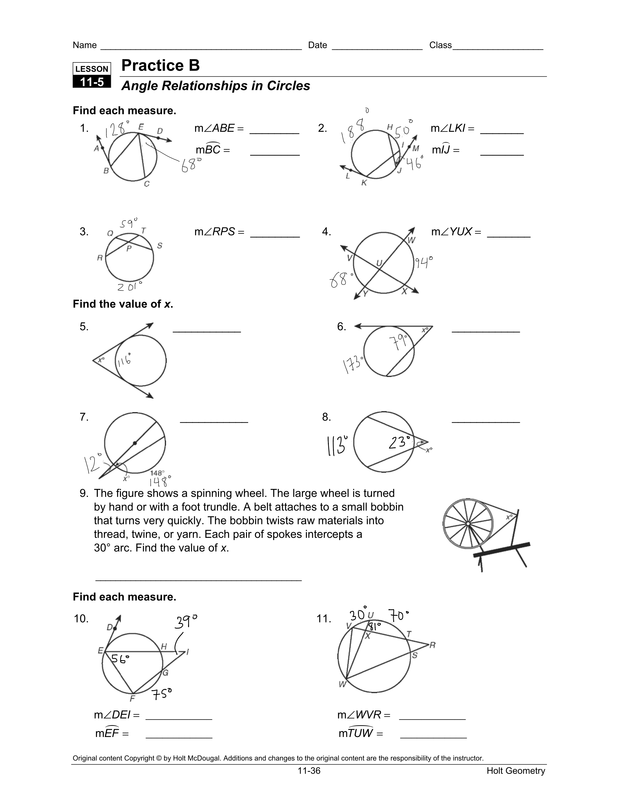
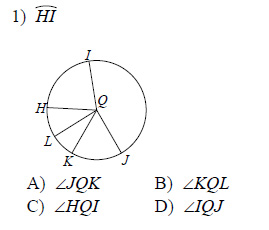
6) Major arc for ∠1. A. B. C. 1. 2. 3. ACB. 7) ∠KQL. I. J. K. L. Q. KL. 8) SVT. R. S. T. U. V. Q. ∠SQT. Find the measure of the arc or central angle |
|
Geometry - Central Angles and Arc Measure
.2 U pATlCl9 Dr3i2gVhQtOsq 8rdeYsYe6rpvie1d8.d H QMTaGd8ew xwviEtFhz nIZnzfoivnLintWed PGFeqodmDeAt7rtyH.n. Worksheet by Kuta Software LLC. -5-. Answers to |
|
SFUSD Mathematics Core Curriculum Grade 10
http://www.sfusdmath.org/uploads/2/4/0/9/24098802/sfusd_unit_g.6_circles_and_conics.pdf |
|
Untitled
Homework Review. Draw diagram & show your work! Return Cores! unit 8 9.3 Arcs & Central Angles. Objectives: I can solve problems by applying |
|
Geometry Ch 10 Notes: Circle DRHS 2022
Apr 25 2023 10.1 Arc and Central Angles in Circles. HW: 10.1 Worksheet. 4/21/23. 4 ... the measures of the central angle and the enclosed arc change. Make a ... |
|
Unit 7. Inscribed and central angles
Furthermore in-class 1.7 |
|
8.1 Circles Central Angles and Intercepted Arcs
see that it is what you described in #2 above. Complete a sketch for each Finish for Homework & check. Find the measure of the arc or central angle indicated. |
|
9-2 Measuring Angles and Arcs
The measure of a minor arc is equal to the measure of its related central angle. Therefore the measure of arc AG is 55. ANSWER: minor arc; 55. 25. m. SOLUTION |
|
GEOMETRY R Unit 13 – Circles
Mar 28 2018 Inscribed Angles (Day 2). 1.5. HW 13.1 Part 2. Wednesday. 4/11. Arcs and ... A central angle separates the circle into two arcs with measures. |
|
11.3 Arcs and Central Angles
a minor arc and a semicircle. 2. Draw a circle with a pair of congruent arcs. 3. What is the difference between arc measure and. |
|
Untitled
Per: ** This is a 2-page document! **. 2. A. D 164°. B C. X = X = 4. 6. Unit 10: Circles. Homework 2: Central Angles & Arc Measures. |
|
Untitled
Homework Review. Draw diagram & show your work! Return Cores! Unit 8 9.3 Arcs & Central Angles Directions: Find each angle and arc measures. 1. 2. |
|
Untitled
2. 11. If mZMPL = 63" find each measure. SA. C n. Intro to Circles |
|
11-Arcs and Central Angles.pdf
Arcs and Central Angles 2) ?1. H. I. J. 1. Name the central angle of the given arc. ... Find the measure of the arc or central angle indicated. |
|
Circles – Central Angles
Circles – Central Angles. G.C.A.2. Hw Section 12.3. Name__________________. Geometry. Page 1 of 2 #1) Determine the arc measure. . ? = ______. |
|
Unit 10 Test Study Guide (Circles)
2. Find the area and circumference of the circle to the right. d=16.6. A=YR (8?3) ². C= 16.690 Topic 3: Central Angles. 6. Find each arc measure. |
|
Solutions For Homework #2
If both ascending and descending passes are used the satellite swath crosses the equator twice in every orbit |
|
If an angle is inscribed in a circle then the measure of the angle
If two inscribed angles of a circle intercept the same arc or congruent arcs then the angles 2. (If minor arcs are |
|
Find the value of x. 1. SOLUTION: The sum of the measures of the
2. SOLUTION: The sum of the measures of the central angles of a circle with no interior points in common is 360. ANSWER: 10-2 Measuring Angles and Arcs ... |
|
Untitled
Kuta Software - Infinite Algebra 2. Name. Arc Length and Sector Find the measure of the arc or angle in Oo given mCD= 108° and mBE = 100°. 20. m ABC. |
|
Central Angles - Circles - GEOMETRY
#7) From the given diagram determine whether the arcs are Major Minor or Semi-Circle To describe the arc without giving it way through notation we will |
|
Solved 102 HW Name: Unit 10: Circles Date: Per: Homework 2
Question: 10 2 HW Name: Unit 10: Circles Date: Per: Homework 2: Central Angles Arc Measures ** This is a 2-page document! " Directions: Find the following |
|
Unit 10 homework 2 central angles and arc measures {MRTXF9}
Unit 10 homework 2 central angles and arc measures ) Divide the intercepted arc AB by 2 Two sides are radi and vertex at center of circle |
|
Unit 10: Circles Homework 2 Answer Key I55QNV
Per: Homework 2: Central Angles Arc Measures ** This is a 2-page document Pdf from AA 1Name: Laci White Unit 10: Date: Circles Homework 2: Bell: |
|
Unit 10 homework 6 arc and angle measures answers (DSMMI0)
Unit 10 Homework 2 Central Angles and Arc Measures [PDF] Untitled Unit 10 Homework 2 Central Angles and Arc Measures [PDF] Untitled Doctoral Training |
|
Unit 10 Circles Homework 3 Arc Lengths AS1AFB
Unit 10: Circles Homework 3: Arc Lengths Answer Key Pdf - Wakelet Unit 10: circles homework 2: Central angles arc measures and arc length |
|
Unit 10 Circles Homework 2 (7R2WZW)
Unit 10 Circles Homework 2 Central Angles Arc Measures [PDF] Untitled Unit 10 Circles Homework 2 Central Angles Arc Measures [PDF] Untitled |
|
Unit 10 Circles Homework 2 Central Angles Arc Measures Answer Key
Results 1 - 24 of 48 · Recorded with Answer The value of x is 16 degrees and the measure of the arc DFG for circles of homework 2 are 1 6 |
|
Central angles and arc measures - YouTube
11 mai 2021 · central angles and arc measures Mark Johnson Mark Johnson 2 48K subscribers Subscribe Durée : 12:51Postée : 11 mai 2021 |
Understanding Central Angles and Arc Measures
Explore the concepts of central angles and arc measures to understand their significance in geometry and trigonometry.
Examples of Central Angles and Arc Measures
Illustrate the relationship between central angles and arc measures:
- Example 1: A central angle of 90 degrees corresponds to a quarter-circle arc.
- Example 2: A central angle of 180 degrees corresponds to a semicircle arc.
- Example 3: A central angle of 360 degrees corresponds to a full-circle arc or circumference.
- Example 4: A central angle of 45 degrees corresponds to an eighth-circle arc.
- Example 5: A central angle of 270 degrees corresponds to a three-quarter-circle arc.
Practice Exercises
Enhance your understanding with these practice exercises:
- Determine the central angle corresponding to an arc measure of 120 degrees.
Correct Answer: 120 degrees - Calculate the arc length corresponding to a central angle of 45 degrees in a circle with a radius of 8 centimeters.
Correct Answer: \( \frac{1}{8} \times 2\pi \times 8 = 2\pi \) centimeters - Find the arc measure corresponding to a central angle of \( \frac{2}{3} \) radians.
Correct Answer: \( \frac{2}{3} \times \frac{180}{\pi} \) degrees - Given an arc length of 10 meters in a circle with a radius of 5 meters, calculate the central angle.
Correct Answer: \( \frac{10}{5} \) radians or \( \frac{10}{5} \times \frac{180}{\pi} \) degrees - Determine the radius of a circle given a central angle of 60 degrees and an arc length of 6 centimeters.
Correct Answer: \( \frac{6}{60} \times \frac{\pi}{180} \) meters
Case Studies
Explore real-life applications of central angles and arc measures:
- Case Study 1: Designing a Ferris wheel requires understanding central angles to ensure balanced weight distribution and safe rotation.
- Case Study 2: Planning road networks involves calculating arc lengths to determine the curvature of roads and optimize traffic flow.
- Case Study 3: Constructing arch bridges relies on central angles to determine the shape and dimensions of arches for structural stability.
- Case Study 4: Programming animations in video games utilizes arc measures to create realistic movements and trajectories for characters and objects.
- Case Study 5: Analyzing planetary orbits in astronomy employs central angles to model the positions and movements of celestial bodies in space.
Important Notes
Key points to remember when studying central angles and arc measures:
- A central angle is formed by two radii of a circle and measures the angle at the center of the circle.
- Arc measure refers to the portion of the circumference of a circle intercepted by a central angle.
- The arc length formula is given by \( \text{Arc Length} = \text{Central Angle} \times \text{Radius} \times \frac{\pi}{180} \).
- The arc measure formula is given by \( \text{Arc Measure} = \text{Central Angle} \times \frac{\pi}{180} \).
- Understanding central angles and arc measures is essential for various fields, including engineering, architecture, physics, and computer graphics.
By internalizing these notes, you can apply central angles and arc measures effectively in problem-solving and real-world scenarios.
Subcategories
Dive deeper into specific aspects of central angles and arc measures:
- Trigonometric Relationships: Explore the trigonometric functions and identities related to central angles and arc measures, such as sine, cosine, and tangent.
- Geometric Constructions: Learn techniques for constructing central angles and measuring arc lengths using geometric tools and principles.
- Application in Geometry: Discover how central angles and arc measures are used in geometric proofs, theorems, and problem-solving strategies.
- Advanced Topics: Delve into advanced concepts, such as sector areas, segment lengths, and circular motion, related to central angles and arc measures.
- Interdisciplinary Connections: Investigate the interdisciplinary applications of central angles and arc measures in fields such as art, architecture, navigation, and robotics.
Exploring these subcategories will deepen your understanding of central angles and arc measures and their relevance in various disciplines.
Step-by-Step Guide
Follow these steps to master central angles and arc measures:
- Review the basic concepts of circles, angles, and trigonometry to establish foundational knowledge.
- Understand the definitions and properties of central angles and arc measures in relation to circles.
- Practice solving problems involving central angles, arc measures, arc lengths, and radius calculations.
- Explore real-life applications and case studies to see how central angles and arc measures are used in different contexts.
- Engage in challenging exercises and problem-solving tasks to strengthen your skills and deepen your understanding.
FAQs
- Q: What is the relationship between a central angle and its corresponding arc measure?
A: The central angle and arc measure have a one-to-one correspondence, where the central angle in degrees equals the arc measure in radians. - Q: How do you calculate the length of an arc?
A: The arc length is calculated by multiplying the central angle (in radians) by the radius of the circle and the constant \( \frac{\pi}{180} \). - Q: What are some common applications of central angles and arc measures?
A: Applications include navigation systems, architectural designs, animation software, mechanical engineering, and astronomy.
Multiple Choice Questions
- What is the measure of a central angle that intercepts an arc of length 4π in a circle with a radius of 2?
Correct Answer: 360 degrees - Which formula is used to calculate the arc length?
Correct Answer: Arc Length = Central Angle × Radius × \( \frac{\pi}{180} \) - What is the arc measure of a semicircle?
Correct Answer: 180 degrees
About the Topic
The study of central angles and arc measures is essential in geometry, trigonometry, and various applied sciences. It provides insights into the geometry of circles, angular measurements, and spatial relationships, with wide-ranging applications in engineering, architecture, physics, and technology.
Key Elements to Remember
1. A central angle is an angle formed by two radii of a circle, with its vertex at the center of the circle.
2. Arc measure refers to the portion of the circumference of a circle intercepted by a central angle.
3. The arc length formula involves multiplying the central angle (in radians) by the radius of the circle.
4. Understanding central angles and arc measures is crucial for solving problems in geometry, trigonometry, physics, and engineering.
5. Practice, exploration of real-world applications, and interdisciplinary connections enhance mastery of central angles and arc measures.
|
Homework KEY
7 1 - HW Name: 7- Circle Angles and Arcs Date: Central Angles Homework TALVELUT 34 22 1 Identify and name each of the following from oo Be sure to |
|
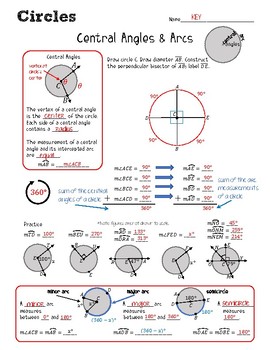
102 Central Angles and Arcs
Minor Arc measure = central angle measure Major Arc measure = 360 - central angle measure Semicircle measure = If 2 inscribed angles of a circle intercept the same arc, then the inscribed angles Homework for Tonight pg 655: 3-10 |
|
Central-angles-hw-key-2pdf
7 - Circle Angles and Arcs 7 1 - HW Name: NUTI Date: Central Angles Homework EVODOTTICOANS TO T Find each measure IL is a diameter 2 mík 30° |
|
The sum of the measures of the central angles of a circle with no
ANSWER: a 79 2 b 28 8 c major arc is a diameter of Find each measure eSolutions Manual - Powered by Cognero Page 2 10-2 Measuring Angles and Arcs |
|
STUDENT TEXT AND HOMEWORK HELPER
segments and angles of circles choosing from a variety of tools (5)(C) Use the circle are equidistant i Central angle – an angle whose Problem 2 The measure of the arc formed by two adjacent arcs is the sum of the measures of the two |
|
113 Arcs and Central Angles
measure of a major arc measure of a minor arc major arc minor arc 11 3 Arcs and Central Angles Find the measures of the arcs Are the arcs congruent? 1 BC s and EF s 2 BC s and CD s 3 CD Homework Help Extra Practice See p |
|
Day 2 - 93 Arcs and Central Anglespdf
Warm Up 2 HW Review 3 Arcs and Central Angles Notes 4 Classwork 5 Exit Ticket Objective: I can find the measure of a specific arc or central angle of a |
|
Circles – Central Angles
Page 1 of 2 41° 100° 55° #2) Determine the arc measure Circles – Central Angles G C A 2 Hw Section 12 3 Name__________________ |
|
Geometry_10-2pdf
the circle, so the length of an arc is a part of the circumference ffi Arc Longth High School say they speDd on homework each night, 1? lfyou were Lesson ' 10-2 Angles and Arcs 533 CRITICAL THINKING Central angles 1, 2, and 3 have |
|
Unit 10 Notes Keypdf
Lesson 2: Central Angles and Arcs > Lesson 3: Inscribed Angles and Arcs Lesson 4: Proving Circles Similar and Measures of Arcs Lesson 5: Circles, Chords, |