 Cours RDM: Torsion simple
Cours RDM: Torsion simple
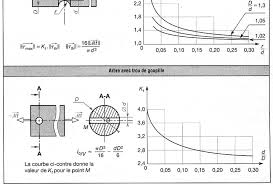
La poutre est supposée à section circulaire constante et de poids négligé. Le Figure 5.5 : Moment quadratique polaire en fonction de la section. Page 6 ...
 Cours RDM : Flambement des poutres comprimées
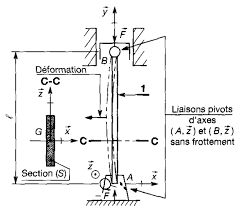
Cours RDM : Flambement des poutres comprimées
Pré-requis. Compression. Moments quadratiques par rapport aux axes de section. Eléments de contenu. Elancement. Charge critique. Condition de résistance
 Sans titre
Sans titre
Le solide est idéal : matériau homogène isotrope
 Cours de Mécanique des Milieux Continus
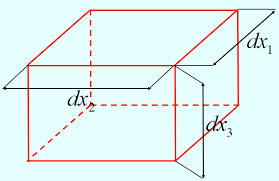
Cours de Mécanique des Milieux Continus
de section droite circulaire? Donner l'expression du tenseur Il en est de même pour le moment quadratique car la section droite de la poutre est constante.
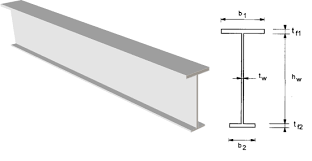 Table des Matières
Table des Matières
On définit le moment d'inertie ou moment quadratique d'une section comme le degré de Section rectangulaire. Section circulaire. Section composée. (en –I–) ...
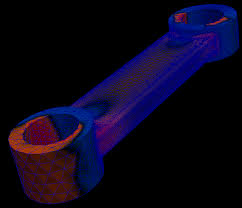 Résistance Des Matériaux
Résistance Des Matériaux
moment quadratique de sa section droite est IGz = 328cm4. Q3. Calculer dans ... Formulaire de trigonométrie circulaire. A. 1. B x. M. H. K cos(x) sin(x) tan(x).
 RDM : FLEXION des POUTRES
RDM : FLEXION des POUTRES
Pour caractériser ce comportement on utilise une grandeur appelée moment quadratique : Pour une section circulaire. IGz = . . 4. 64 x y z h b. Page 6. RDM ...
 Flexion et torsion dun tube rectangulaire droit
Flexion et torsion dun tube rectangulaire droit
On impose les conditions de géométrie du tube (hauteur largeur et épaisseur
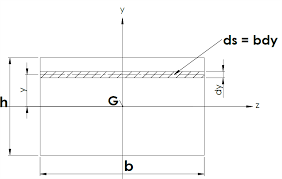 = = = = ds = =
= = = = ds = =
Définition: Moment quadratique par rapport à l'ax. • Poutre à section rectangulaire: Premier calcul: = ds = dy. La primitive de est.
 = = = = ds = =
= = = = ds = =
Définition: Moment quadratique par rapport à l'ax. • Poutre à section rectangulaire: Premier calcul: = ds = dy. La primitive de est.
 ?= dsz ?= dsy = ?
?= dsz ?= dsy = ?
1.1) Section circulaire : 1.2) Section elliptique : 1.3) Section rectangulaire : 1.4) Section demi-circulaire : Moment quadratique / axe (G y.
 RDM : FLEXION des POUTRES
RDM : FLEXION des POUTRES
situant sur l'axe Z on note le moment quadratique : IGz. Pour une section rectangulaire : IGz = .?. 3. 12. Pour une section circulaire.
 TORSION
TORSION
On exerce un moment MG1 dans la section droite (S1) et on mesure l'angle de rotation Le moment quadratique polaire de la surface (S) par rapport à l'axe.
 PROPRIÉTÉS DES SECTIONS
PROPRIÉTÉS DES SECTIONS
Moment d'inertie;. • Module de section;. • Rayon de giration. 8.1.2 Surface neutre et axe neutre. Lorsqu'une poutre est soumise à des forces qui tendent à
 Banque de Brevets: petits exercices avec résultats: théorie des
Banque de Brevets: petits exercices avec résultats: théorie des
16 mai 2012 1.257brevet 610 bis : Calcul numérique du moment quadratique en torsion d'une poutre de section circulaire creuse .
 ENSIM 4A Statique des poutres ( résistance des matériaux )
ENSIM 4A Statique des poutres ( résistance des matériaux )
12 févr. 2019 Pour cette démonstration vous noterez qu'est effectué un développement ... exemple Le calcul du moment polaire d'une section circulaire est ...
 Catalogue des tubes
Catalogue des tubes
Dimensions et caractéristiques des profils creux de section circulaire. I/V. Moment d'inertle de flexion. Module de Module de flexion flexion plastique.
 RESISTANCE DES MATERIAUX
RESISTANCE DES MATERIAUX
Pour chaque type de section : • Calculer le moment quadratique I0 s'il n'est pas donné. Section circulaire. Section rectangulaire. Section en T.
 Chapitre 8 : Torsion uniforme
Chapitre 8 : Torsion uniforme
TORSION (poutre à section circulaire "arbres") Généralisation : Couronne ou section circulaire creuse ... cylindrique) et que le moment de.
 [PDF] Moments quadratiques
[PDF] Moments quadratiques
Définition: Moment quadratique par rapport à l'ax • Poutre à section Poutre à section carrée de cotée "a" : Poutre à section circulaire :
 [PDF] PROPRIÉTÉS DES SECTIONS
[PDF] PROPRIÉTÉS DES SECTIONS
Pour les sections complexes ou composées de plusieurs sections simples le moment d'inertie est égal à la somme des moments d'inertie de chacune des sections
 [PDF] Table des Matières
[PDF] Table des Matières
Calculer analytiquement le moment quadratique polaire IO de la section S représentée sur la figure ci-contre Exercice N°4 1- Exprimer le moment d'inertie
 [PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
[PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
Calculer le moment statique et le moment d'inertie d'une section circulaire de diamètre d par rapport aux deux axes vertical (y) et horizontal (x) passant
 [PDF] RMChap4(MomentInertie)pdf
[PDF] RMChap4(MomentInertie)pdf
Ces caractéristiques sont : aire des sections transversales moment statique moment d'inertie moment résistant rayon de giration
 (PDF) Moment quadratique Brahim Elidrissi - Academiaedu
(PDF) Moment quadratique Brahim Elidrissi - Academiaedu
Moment quadratique Moment quadratique par rapport à l'axe z : r R Section rectangulaire : Section circulaire : Section circulaire creux :
 Moment quadratique - H7g6fr
Moment quadratique - H7g6fr
Le moment quadratique est une grandeur qui caractérise la géométrie d'une section et se définit par rapport à un axe ou un point
 [PDF] MÉCANIQUE 1/2 - Axes Industries
[PDF] MÉCANIQUE 1/2 - Axes Industries
Masse ponctuelle J = M R 2 Cylindre plein J = 1 2 M R 2 Cylindre annulaire J = 1 2 M ( R1 2 - R2 2 ) Cylindre annulaire mince
 [PDF] RDM-inertiespdf
[PDF] RDM-inertiespdf
Moment statique : c'est la somme des produits des surfaces par le bras de statiques de part et d'autre de cet quadratiques (moments of inertia): on
RDM- TORSION RDM 1/5
TORSION
6ROLGH LGpMO matériau homogène, isotrope, poutre rectiligne, de section constante et circulaire.
IHV MŃPLRQV H[PpULHXUHV dans les sections extrêmes sont modélisables par deux moments opposés,
portés par la ligne moyenne. La poutre est donc soumise à deux torseurs couples:I. DEFINITION
Une poutre est sollicitée à la torsion simple si le torseur associé aux forces de cohésion de la partie droite (II) sur la partie gauche (I) de la poutre peut se réduire en G, barycentre de la section droite (S) à un moment perpendiculaire à (S), tel que:Dans (G,x
,y ,z [Tcoh] = G 0 Mt avecN = 0, Ty = 0, Tz = 0
Mt0, Mfy = 0, Mfz = 0 donc =
G 0Mt 00 00REMARQUE:
[Tcoh] = -T(Actions ext.I) = +T(Actions ext.
II) donc R = 0 et Mt = -MAII. ETUDE DES DEFORMATIONS
On exerce un moment MG1
dans la section droite (S1) et on mesure l'angle de rotation des sections (S ) et (S1) par rapport à (S0). On constate que: x = 1 l1 = ...... = Cte. (S1) (S0) Ligne moyenne MB MA A B x z y G (S MA A MG z y Lf3II I Lf2II I Lf1II I G1 (S1) MG 1G0 (S) (S0)
M' M1'
M1 M 1 1 x l1Génératrice avant
déformationGénératrice après
déformationSection S0 parfaitement encastrée dans 1
RDM- TORSION RDM 2/5
On peut écrire:
1 l1 avec: = angle unitaire de torsion (rad/mm).1 = angle de rotation (S1)/(S0) (en rad).
l1 = distance séparant (S1) à la section de référence (S0) (mm)La courbe donnant l'angle
en fonction du moment MG1 fait apparaître deux zones : IM ]RQH 2$ GH GpIRUPMPLRQ pOMVPLTXH ou
domaine élastique: où l'angle de rotation est proportionnel au moment appliqué. IM ]RQH $% GH GpIRUPMPLRQ SHUPMQHQPH, ou domaine plastique; n'est pas proportionnel à MG1 III. REPARTITION DES CONTRAINTES DANS UNE SECTION DROITEEn un point M, la contrainte de torsion
M est proportionnelle à la distance
de ce point à la ligne moyenne. M = .G. . [Dans (O,x1 ,y1M > 0 si
> 0 et 0] M: contrainte tangentielle due à la torsion (MPa). G: module d'élasticité transversale (de Coulomb) (MPa). : angle de torsion unitaire (rad/mm). : distance de M au centre de la section (mm). La contrainte de torsion est nulle si M est sur la ligne moyenne ( = 0). La fibre neutre est confondue avec la ligne moyenne. La contrainte de torsion est maximale si M est sur la surface du solide ( = R = distance max.): max. = G. .R.IV. MOMENT QUADRATIQUE POLAIRE
Le moment quadratique polaire de la surface (S) par rapport à l'axe (O, z) perpendiculaire en O au plan de cette dernière est: I0 = s) I0: moment quadratique de (S) par rapport a (O,z) (mm4). : distance du point M au point O (mm). S: surface élémentaire entourant le point M(mm2). B MG1 A MA 0Déformation
permanenteDéformation
élastique
max maxM1 M x
1 y z y 1 x z y F G xSection droite
(S) MG0 G0 Mt z y O M x y M S S ODistance de M
ààààO O
Point M
considéréSurface
élémentaire
RDM- TORSION RDM 3/5
MOMENTS QUADRATIQUES PARTICULIERS
Oz x y d Oz x y D d I0 = .d4 32I0= 32
.(D4-d4)
V. ETUDE DES DEFORMATIONS
1- Equation de déformation
Dans le domaine élastique, le moment de torsion Mt est proportionnel à l'angle unitaire de torsion
Mt = G.
.I0 si > 0 Mt > 0Mt: moment de torsion (Nmm).
G: module d'élasticité transversal (de Coulomb) (MPa). : angle de torsion unitaire (rad/mm). I0: moment quadratique de (S) par rapport a (O, x) (mm4). * Voir valeurs de G pour différents matériaux dans cours cisaillement.2- Condition de rigidité
Pour les arbres de grande longueur (arbres de forage de puits de pétrole, arbres de naviresimportants) on évite de trop grandes déformations de torsion qui risqueraient d'engendrer des vibrations
trop importantes pour un fonctionnement correct. A cet effet, on impose un angle unitaire limite de torsion: lim. à ne pas dépasser ( lim: 0,25 °/m, par exemple). lim ou Mt G.Io lim. Mt: moment de torsion (Nmm). G: module d'élasticité transversale (de Coulomb) (MPa). I0: moment quadratique de (S) par rapport à (O,z) (mm4).VI. ETUDE DE LA RESISTANCE
3- Contraintes de torsion
Contrainte de torsion en fonction de Mt:
La contrainte en un point M d'une section
droite est:M = Mt
Io M : contrainte tangentielle due a la torsion (MPa)*.Mt: moment de torsion (Nmm).
I0: moment quadratique polaire de la section droite considérée (mm4). : distance du point M à la fibre neutre (mm). x GM d=2RValeur de
M en un point M
M G MG0 O Mt z y G (S) MO Mt O (S0) M' M x y zSens positif pour l'angle de
rotation l 0 0RDM- TORSION RDM 4/5
4- Contrainte maximale de torsion
Il faut rechercher la section (S) dans laquelle le moment de torsion est maximal. Dans celle-ci la contrainte est maximale au point le plus éloigné de l'axe ( = R). max. = Mtmax Io .R ou max. = Mtmax (I0 R)Tmax.: contrainte maximale tangentielle (MPa)*.
Mt max.: moment de torsion maximale (Nmm).
I0: moment quadratique polaire de la section (S) (mm4). R: distance du point le plus éloigne de la fibre neutre à cette dernière (mm). (I0R): module de torsion (mm3).
* 1 MPa = 1 N/mm2REMARQUE:
Ces relations sont valables uniquement pour les sections circulaires!5- Condition de résistance
Pour des raisons de sécurité, la contrainte de torsion doit rester inférieure à la résistance pratique
au glissement Rpg est le quotient de résistance élastique au glissement Rpg par le coefficient de
sécurité s. (Voir la relation entre Re et Reg dans le cours sur le cisaillement)Rpg = Reg
sRpg: résistance pratique au glissement (MPa).
Reg: résistance élastique au glissement (MPa). s: coefficient de sécurité (sans unité) (voir valeurs dans le cours sur le cisaillement).La condition de résistance est:
max.Rpg ou
Mt max (I0 R) RpgVII. SOLIDE REEL
les arbres présentent généralement de brusques variations de sections (gorges, épaulements,
rainures de clavettes. . .). Au voisinage de ces variations de section, la répartition des contraintes n'est
pas linéaire. Il y a concentration de contrainte. eff. max. = Kt. théorique eff. max.: contrainte maximale effective (MPa). théorique contrainte théorique sans concentration (MPa). Kt: coefficient de concentration de contrainte relatif a la torsion. Kt est déterminé par des tableaux ou abaques (voir les valeurs expérimentales dans tableau).Kt pour rainures de clavettes
Rayon congé
Profondeur rainure
= r c0.5 0.3 0.2 0.1
Coefficient Kt 2.1 2.7 3.5 5.4
c M' MRayon du
congé: r M'M théorique
eff max = Kt. théorique théorique Kt.M théorique
RDM- TORSION RDM 5/5
Kt pour épaulement et congé
0.0 50.1 0.1
50.2 0.2
5 0.31.09 1.3 1.1
8 1.1 51.1 1.1 1.1
1.2 1.6 1.3
5 1.2 51.2 1.1
8 1.1 51.5 1.7 1.4
51.3 1.2
5 1.2 2 1.22 1.8 1.6 1.3
51.3 1.2
5 1.2 2Kt pour gorge
0.0 50.1 0.1
50.2 0.2
5 0.31.02 1.3
51.3 1.5 1.7 1.1
5 1.1 51.05 1.5
51.5 1.7 2.5 1.2 1.2
1.3 1.8 1.7 2.2 2.7 1.3 1.2
5Kt pour arbre avec trou de goupille
d/D 0.0 50.1 0.1
50.2 0.2
5 0.3Kt 1.3
51.3 1.5 1.7 1.1
5 1.1 5 I0/V .d3 16 - d.D² 6MÉTHODE DE CALCUL
1. Calculer
m ou max.2. Analyser la nature ou la géométrie (épaulement, gorge...) et choisir la courbe ou le tableau
correspondant3. Calculer r
c , r D , D d4. Déterminer la valeur de Kt correspondante
5. Calculer
eff. max. = Kt. théorique6. Ecrire la condition de résistance
eff. max.quotesdbs_dbs16.pdfusesText_22[PDF] moment quadratique triangle
[PDF] moment quadratique poutre en t
[PDF] moment quadratique poutre en u
[PDF] moment quadratique formulaire
[PDF] ranger dans l'ordre synonyme
[PDF] modèle de fiche de suivi collège
[PDF] moments et actes fondateurs de la république stmg
[PDF] exemple fiche de suivi
[PDF] fiche de suivi attitude élève
[PDF] modèle de note de synthèse
[PDF] note de synthèse exemple pdf
[PDF] momo petit prince des bleuets lire en ligne
[PDF] ranger des nombres dans l'ordre croissant
[PDF] évaluation théâtre seconde
