 Cours RDM: Torsion simple
Cours RDM: Torsion simple
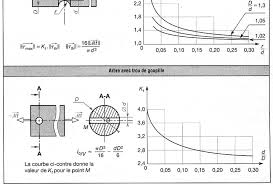
La poutre est supposée à section circulaire constante et de poids négligé. Le Figure 5.5 : Moment quadratique polaire en fonction de la section. Page 6 ...
 Cours RDM : Flambement des poutres comprimées
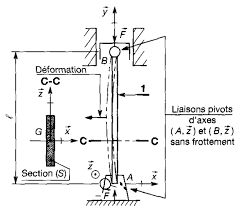
Cours RDM : Flambement des poutres comprimées
Pré-requis. Compression. Moments quadratiques par rapport aux axes de section. Eléments de contenu. Elancement. Charge critique. Condition de résistance
 Sans titre
Sans titre
Le solide est idéal : matériau homogène isotrope
 Cours de Mécanique des Milieux Continus
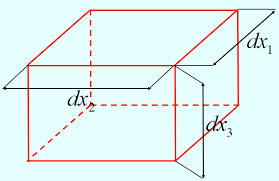
Cours de Mécanique des Milieux Continus
de section droite circulaire? Donner l'expression du tenseur Il en est de même pour le moment quadratique car la section droite de la poutre est constante.
 Table des Matières
Table des Matières
On définit le moment d'inertie ou moment quadratique d'une section comme le degré de Section rectangulaire. Section circulaire. Section composée. (en –I–) ...
 TORSION
TORSION
Tmax.: contrainte maximale tangentielle (MPa)*. Mt max.: moment de torsion maximale (Nmm). I0: moment quadratique polaire de la section (S) (mm4)
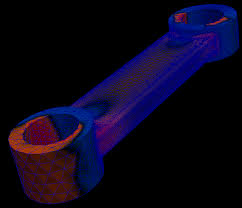 Résistance Des Matériaux
Résistance Des Matériaux
moment quadratique de sa section droite est IGz = 328cm4. Q3. Calculer dans ... Formulaire de trigonométrie circulaire. A. 1. B x. M. H. K cos(x) sin(x) tan(x).
 RDM : FLEXION des POUTRES
RDM : FLEXION des POUTRES
Pour caractériser ce comportement on utilise une grandeur appelée moment quadratique : Pour une section circulaire. IGz = . . 4. 64 x y z h b. Page 6. RDM ...
 Flexion et torsion dun tube rectangulaire droit
Flexion et torsion dun tube rectangulaire droit
On impose les conditions de géométrie du tube (hauteur largeur et épaisseur
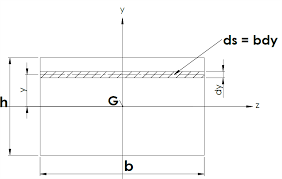 = = = = ds = =
= = = = ds = =
Définition: Moment quadratique par rapport à l'ax. • Poutre à section rectangulaire: Premier calcul: = ds = dy. La primitive de est.
 = = = = ds = =
= = = = ds = =
Définition: Moment quadratique par rapport à l'ax. • Poutre à section rectangulaire: Premier calcul: = ds = dy. La primitive de est.
 ?= dsz ?= dsy = ?
?= dsz ?= dsy = ?
1.1) Section circulaire : 1.2) Section elliptique : 1.3) Section rectangulaire : 1.4) Section demi-circulaire : Moment quadratique / axe (G y.
 RDM : FLEXION des POUTRES
RDM : FLEXION des POUTRES
situant sur l'axe Z on note le moment quadratique : IGz. Pour une section rectangulaire : IGz = .?. 3. 12. Pour une section circulaire.
 TORSION
TORSION
On exerce un moment MG1 dans la section droite (S1) et on mesure l'angle de rotation Le moment quadratique polaire de la surface (S) par rapport à l'axe.
 PROPRIÉTÉS DES SECTIONS
PROPRIÉTÉS DES SECTIONS
Moment d'inertie;. • Module de section;. • Rayon de giration. 8.1.2 Surface neutre et axe neutre. Lorsqu'une poutre est soumise à des forces qui tendent à
 Banque de Brevets: petits exercices avec résultats: théorie des
Banque de Brevets: petits exercices avec résultats: théorie des
16 mai 2012 1.257brevet 610 bis : Calcul numérique du moment quadratique en torsion d'une poutre de section circulaire creuse .
 ENSIM 4A Statique des poutres ( résistance des matériaux )
ENSIM 4A Statique des poutres ( résistance des matériaux )
12 févr. 2019 Pour cette démonstration vous noterez qu'est effectué un développement ... exemple Le calcul du moment polaire d'une section circulaire est ...
 Catalogue des tubes
Catalogue des tubes
Dimensions et caractéristiques des profils creux de section circulaire. I/V. Moment d'inertle de flexion. Module de Module de flexion flexion plastique.
 RESISTANCE DES MATERIAUX
RESISTANCE DES MATERIAUX
Pour chaque type de section : • Calculer le moment quadratique I0 s'il n'est pas donné. Section circulaire. Section rectangulaire. Section en T.
 Chapitre 8 : Torsion uniforme
Chapitre 8 : Torsion uniforme
TORSION (poutre à section circulaire "arbres") Généralisation : Couronne ou section circulaire creuse ... cylindrique) et que le moment de.
 [PDF] Moments quadratiques
[PDF] Moments quadratiques
Définition: Moment quadratique par rapport à l'ax • Poutre à section Poutre à section carrée de cotée "a" : Poutre à section circulaire :
 [PDF] PROPRIÉTÉS DES SECTIONS
[PDF] PROPRIÉTÉS DES SECTIONS
Pour les sections complexes ou composées de plusieurs sections simples le moment d'inertie est égal à la somme des moments d'inertie de chacune des sections
 [PDF] Table des Matières
[PDF] Table des Matières
Calculer analytiquement le moment quadratique polaire IO de la section S représentée sur la figure ci-contre Exercice N°4 1- Exprimer le moment d'inertie
 [PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
[PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
Calculer le moment statique et le moment d'inertie d'une section circulaire de diamètre d par rapport aux deux axes vertical (y) et horizontal (x) passant
 [PDF] RMChap4(MomentInertie)pdf
[PDF] RMChap4(MomentInertie)pdf
Ces caractéristiques sont : aire des sections transversales moment statique moment d'inertie moment résistant rayon de giration
 (PDF) Moment quadratique Brahim Elidrissi - Academiaedu
(PDF) Moment quadratique Brahim Elidrissi - Academiaedu
Moment quadratique Moment quadratique par rapport à l'axe z : r R Section rectangulaire : Section circulaire : Section circulaire creux :
 Moment quadratique - H7g6fr
Moment quadratique - H7g6fr
Le moment quadratique est une grandeur qui caractérise la géométrie d'une section et se définit par rapport à un axe ou un point
 [PDF] MÉCANIQUE 1/2 - Axes Industries
[PDF] MÉCANIQUE 1/2 - Axes Industries
Masse ponctuelle J = M R 2 Cylindre plein J = 1 2 M R 2 Cylindre annulaire J = 1 2 M ( R1 2 - R2 2 ) Cylindre annulaire mince
 [PDF] RDM-inertiespdf
[PDF] RDM-inertiespdf
Moment statique : c'est la somme des produits des surfaces par le bras de statiques de part et d'autre de cet quadratiques (moments of inertia): on
PROPRIÉTÉS DES SECTIONS
8.1.1 Généralités
Dans l'étude des déflexions des poutres ainsi que du flambage des colonnes, on est amené à utiliser
l'une ou l'autre des propriétés des sections droites, qui sont des caractéristiques purement
géométriques. On retrouve: • Axe neutre d'une surface; • Centre de gravité d'une surface; • Moment statique d'une surface; • Moment d'inertie; • Module de section; • Rayon de giration.8.1.2 Surface neutre et axe neutre
Lorsqu'une poutre est soumise à des forces qui tendent à la courber, les fibres situées a u-dessus (ouau-dessous) d'un certain plan de la poutre sont en compression et elles se raccourcissent, tandis que
les fibres situées au-dessous (ou au-dessus) de ce plan sont tendues et elles s'allongent. Le plan
intermédiaire en question est appelé surface neutre de la poutre (voir figure 8.1).Pour une section droite de la poutre, la li
gne correspondant à la surface neutre s'appelle axe neutrede cette section. L'axe neutre passe toujours par un point particulier "cg" de la section droite d'une
poutre nommé centroïde ou centre de gravité de cette section. 137Axe neutre (A.N.): C'est le plan qui ne subit aucun allongement pendant la flexion d'une poutre.
Fig. 8.1
L'axe neutre A.N. passe par le centre de gravité ou centroïde.8.1.3 Centre de gravité (cg)
Le centre de gravité (cg) ou centroïde d'un corps ou d'une surface est un point imaginaire où toute
cette surface peut être considérée comme concentrée. C'est aussi le point où le poids d'un corps est
concentré.Si un corps est homogène, c'est-à-dire constitué d'un seul matériau, le cg dépend seulement de la
forme du corps. Si un corps possède un axe de symétrie, son cg est situé sur cet axe (fig. 8.2).
Fig. 8.2
138L'axe de symétrie partage le corps en deux parties de même surface, de même poids. Si un corps
possède au moins deux axes de symétrie (ou médiane), son cg se trouve au point d'intersection de
ces axes. Le cg n'est pas toujours dans la matière. La figure 8.3 illustre le centre de gravité de
différentes surfaces régulièrement utilisées.Fig. 8.3
La position de quelques autres surfaces est donnée dans les tableaux à la fin du chapitre. D'autres cas
particuliers peuvent être retrouvés dans les "Handbooks" ou livres spécialisées. 1398.2 MOMENT D'INERTIE
8.2.1 Moment d'inertie
Considérons une surface plane A dans laquelle
un élément de surface a i infiniment petit est indiqué. Cet élément se trouve à une distance d i d'un axe quelconque "o". On appelle moment d'inertie I i de l'élément de surface a i par rapport à l'axe considéré "o", le produit de cet élément par le carré de la distance d i A a i d i oFig. 8.7
I i(o) = a i x d i 2 (8.3 a) Si la surface A est subdivisée en N éléments infiniment petits a 1 , a 2 , a 3 , ... , a N dont les distances respectives à l'axe sont d 1 , d 2 , d 3 , ... , d N alors le moment d'inertie de cette surface par rapport au même axe "o" est donné par la relation suivante: I o = I 1(o) + I 2(o) + ... + I N(o) I o = a 1 d 1 2 + a 2 d 2 2 + ... + a N d N 2 I o = a i d i 2 [m 4 ] (8.3) Le moment d'inertie des sections droites est d'une grande importance dans la conception des poutreset colonnes. Les tableaux à la fin du chapitre portant sur les propriétés des sections donnent des
valeurs des moments d'inertie de plusieurs profilés d'acier fréquemment utilisés dans la construction.
140Les autres moments d'inertie peuvent être trouvés dans des "handbooks". La figure suivante donne
quelques moments d'inertie de figures communes. cg axe b h I cg b h 3 12 cg axe I cg d 4 64b h cg axe I cg b h 3 36
Fig. 8.8
8.2.2 Théorème des axes parallèles
Si on connaît le moment d'inertie d'une surface par rapport à un axe qui passe par son centre de
gravité, on peut connaître son moment d'inertie par rapport à tout autre axe parallèle à ce dernier. Il
suffit d'ajouter la quantité As 2à son I
cgThéorème des axes parallèles:
I = I cg + As 2 (8.4) où s = distance entre l'axe choisi et l'axe qui passe par le cg.A = aire de la section
I cg = moment d'inertie par rapport à un axe qui passe par le cg. 141EXEMPLE 8.2: Calculer le moment d'inertie du rectangle ci-dessous par rapport à l'axe z passant par sa base.
Solution:
I z = I cg + As 2 b h 3 12 + (bh) h 2 2 b h 3 12 bh 3 4 b h 3 3 cg b h z h/2Fig. 8.9
Pour les sections complexes ou composées de plusieurs sections simples, le moment d'inertie estégal à la somme des moments d'inertie de chacune des sections. Si la surface composée possède une
surface creuse, le moment de la section creuse est alors négatif. Dans le cas des surfaces composées,
le théorème des axes parallèles est alors très utile. Comme par exemple, la section en T du premier
exemple, si on veut savoir le moment d'inertie de la surface totale, on doit utiliser le théorème, c'est
ce que nous ferons dans le prochain exemple. EXEMPLE 8.3: Calculer le moment d'inertie par rapport à l'axe neutre de la section en T ci- dessous. (fig. 8.10)Solution:
Nous avions déjà trouvé le cg de la surface totale dans le premier exemple, on sait que l'axe neutre passe par le centre de gravité. Maintenant on veut le moment d'inertie par rapport à cet axe. I AN = IAN(surface 1)
+ IAN(surface 2)
IAN(surface 1)
= I cg1 + A 1 s 1 2 IAN(surface 2)
= I cg2 + A 2 s 2 2 1 cm4,5 cm
A 22,59 cm
2 cm 5 cm 6 cm A.N. cg A 1Fig. 8.10
142I cg1
2 cm (5 cm)
3 12 = 20,833 cm 4 et I cg26 cm (2 cm)
3 12 = 4 cm 4 IAN(surf 1)
= 20,833 cmquotesdbs_dbs16.pdfusesText_22[PDF] moment quadratique triangle
[PDF] moment quadratique poutre en t
[PDF] moment quadratique poutre en u
[PDF] moment quadratique formulaire
[PDF] ranger dans l'ordre synonyme
[PDF] modèle de fiche de suivi collège
[PDF] moments et actes fondateurs de la république stmg
[PDF] exemple fiche de suivi
[PDF] fiche de suivi attitude élève
[PDF] modèle de note de synthèse
[PDF] note de synthèse exemple pdf
[PDF] momo petit prince des bleuets lire en ligne
[PDF] ranger des nombres dans l'ordre croissant
[PDF] évaluation théâtre seconde
