[PDF] Résumé des propriétés des fonctions trigonométriques

View - Download Résumé des propriétés des fonctions trigonométriques

Previous PDF

Next PDF

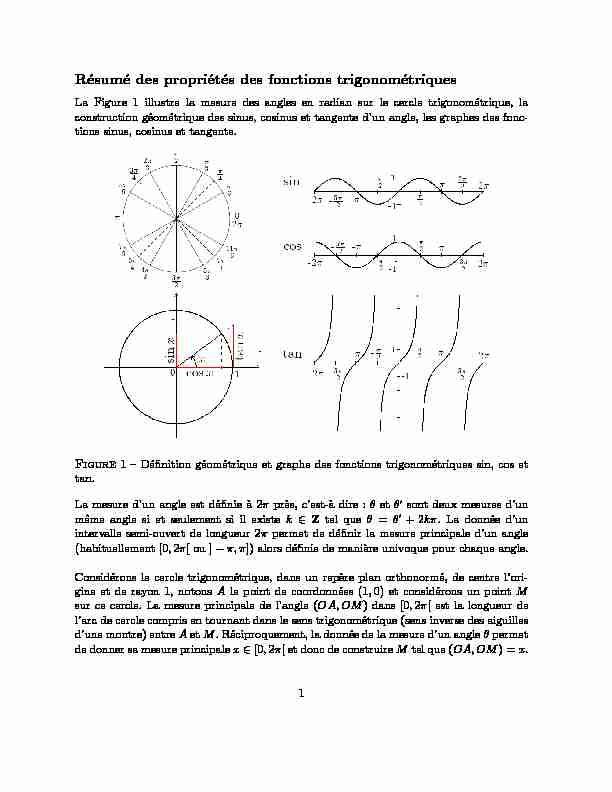Resume des proprietes des fonctions trigonometriques La Figure 1 illustre la mesure des angles en radian sur le cercle trigonometrique, la construction geometrique des sinus, cosinus et tangente d'un angle, les graphes des fonc-

tions sinus, cosinus et tangente.Figure1 { Denition geometrique et graphe des fonctions trigonometriques sin, cos et

tan. La mesure d'un angle est denie a 2pres, c'est-a dire :et0sont deux mesures d'un m^eme angle si et seulement si il existek2Ztel que=0+ 2k. La donnee d'un intervalle semi-ouvert de longueur 2permet de denir la mesure principale d'un angle (habituellement [0;2[ ou ];]) alors denie de maniere univoque pour chaque angle. Considerons le cercle trigonometrique, dans un repere plan orthonorme, de centre l'ori- gine et de rayon 1, notonsAle point de coordonnees (1;0) et considerons un pointM sur ce cercle. La mesure principale de l'angle (OA;OM) dans [0;2[ est la longueur de l'arc de cercle compris en tournant dans le sens trigonometrique (sens inverse des aiguilles d'une montre) entreAetM. Reciproquement, la donnee de la mesure d'un anglepermet de donner sa mesure principalex2[0;2[ et donc de construireMtel que (OA;OM) =x. 1 On denit les fonctions cos et sin de la maniere suivante. Soitx2R. On note alors l'angle de mesurex. Les coordonnees deMtel que (OA;OM) =denissent alors cosxet sinx:M= (cosx;sinx). Les fonctions sin et cos sont donc denies sur toutRa valeurs dans [1;1]. Comme deux reels dierant d'un multiple de 2sont deux mesures d'un m^eme angle et denissent donc le m^eme pointM, leur cosinus et leur sinus sont egaux. Les fonctions cos et sin sont donc 2-periodiques : pour toutx2R, pour toutk2Z, sin(x+ 2k) = sin(x) et cos(x+ 2k) = cos(x). Ces fonctions associent donc la m^eme valeur a toutes mesures d'un m^eme angle.Quelques valeurs particulieres : cos0 = 1;cos2 = 0;cos=1;cos32 = 0; sin0 = 0;sin2 = 1;sin= 0;sin32 =1; cos 6 =p3 2 ;cos4 =p2 2 ;cos3 =12 sin 6 =12 ;sin4 =p2 2 ;sin3 =p3 2 :Comme cosx= 0()x=2 +k;aveck2Z; la fonction-periodique tan =sincos est denie sur D tan=Rnn2 +kjk2Zo :Formulaire : cos(a) = cosa;sin(a) =sina;tan(a) =tana; cos(a) =cosa;sin(a) = sina;tan(a) =tana; cos(+a) =cosa;sin(+a) =sina;tan(+a) = tana; cos( 2 a) = sina;sin(2 a) = cosa;tan(2 a) = cotana=1tana; cos( 2 +a) =sina;sin(2 +a) = cosa;tan(2 +a) =cotana=1tana: cos(a+b) = cosacosbsinasinb;sin(a+b) = sinacosb+ cosasinb; cos(ab) = cosacosb+ sinasinb;sin(ab) = sinacosbcosasinb:

Propriete fondamentale :8a2R;cos2a+ sin2a= 1.Le formulaire et les valeurs particulieres permettent de retrouver toutes les valeurs de

cos, sin et tan de tous les angles materialises sur le cercle trigonometrique de la Figure 1 (en haut a gauche). 2 Les fonctions trigonometriques classiques induisent des bijections (voir Figures 1 et 2) : sin induit une bijection en tre[ 2 ;2 ] et [1;1], c osinduit une bijection en tre[0 ;] et [1;1], t aninduit une bijection en tre] 2 ;2 [ etR. Les bijections reciproques sont respectivement notees : a rcsin: [ 1;1]![2 ;2 a rccos: [ 1;1]![0;], a rctan: R!]2 ;2 [.Figure2 { Graphes des restrictions bijectives des fonctions sin, cos et tan et des bijections reciproques arcsin, arccos et arctan.

Resume de cours sur les nombres complexes

Le nombre imaginaireiest introduit comme solution dex2=1 et verie donc i 2=1: On construit l'ensembleCdes nombres complexes qui est en bijection avecRRa l'aide de iet des proprietes des operations (multiplication, addition) heritees de celles surR. Ainsi un nombre complexe s'ecrit sous sa forme dite \cartesienne" :z=a+ibavecaetbdes reels. Le reela=<(z) est appele la \partie reelle" dezetb==(z) sa \partie imaginaire". Le complexezest represente dans le plan (muni d'un repere cartesien d'origineO) par un unique pointM= (a;b) appele \image" dez. Reciproquement, le complexezest appele \l'axe" deM(voir Figure 3, panel de gauche). Le modulejzjdezest la distance entreOetM, soitja+ibj=pa

2+b22R+. Pourz6= 0,

c'est-a-direa6= 0 oub6= 0, un argument dezest une mesure de l'angle entre le demi-axe des abscisses positives [O;x) et la demi-droite [O;M). En prescrivant un intervalle de longueur 2, on denit l'argument (principal) dezcomme l'unique mesure de cet angle appartenant a l'intervalle prescrit, alors noteArg(z). 3

Figure3 {

Conjugue

Le conjugue dez=a+ibest le complexe z=aib. L'image de zest le symetrique de l'image dezpar rapport a l'axe des abscisses (voir Figure 3, panel de droite). Pour tous complexeszetz0, on a :zz=jzj2;z+z0= z+z0; zz 0=z z0;z n= (z)n; z+ z=<(z); zz0= 2i=(z); zest reel()z= z; zest imaginaire pur()z=z:Forme polaire Un complexe de modulejzj=r >0 et d'arguments'ecrit sous sa forme polaire z=rei Les proprietes de l'exponentielle reelle sont conservees dansC.

On a :z=rei=rcos+irsin. Ainsi :i= ei2

;1 = ei;i= ei32 = ei2 :Pour touszetz0complexes :jzz0j=jzjjz0j; Arg(zz0) =Arg(z) +Arg(z0) + 2kouk2Z: jznj=jzjn; Arg(zn) =nArg(z) + 2kouk2Z:4 Trouver l'argument d'un complexe sous forme cartesienne Soitz=a+ib,aetbreels. On peut calculer son module :jzj=pa 2+b2.

On trouve son argumenten resolvant :

jzjcos=a; jzjsin=b: On peut exprimer les solutions de plusieurs manieres en utilisant les bijections reciproques des fonctions trigonometriques. On suppose quea6= 0 etb6= 0 (dans le cas contraire, il est tres facile de trouver un argument parmi 0;2 ;;32 selon le cas... laisse en exercice). =8 :arctan ba + 2ksia >0 + arctanba + 2ksia <0=8 :arccos ajzj+ 2ksib >0 arccosajzj+ 2ksib <0=8 >:arcsin bjzj+ 2ksia >0 arcsinbjzj+ 2ksia <0

Racinen-ieme d'un complexe

Il existensolutions complexes dezn= 1 :

U n=n e i2kn jk2 f0;1;2;:::;n1go appelees racinesn-iemes de l'unite. Les images des racinesn-iemes de l'unite sont les som- mets du polygone regulier anc^otes inscrit dans le cercle trigonometrique et admettant 1 pour sommet. Pour toutz0=jz0jei2C, il existensolutions complexes dezn=z0: S n=n jz0j1n ei+2kn jk2 f0;1;2;:::;n1go Les images des racinesn-iemes dezsont les sommets du polygone regulier anc^otes inscrit dans le cercle de centreOet de rayonjz0j1n et admettantjz0j1n ein pour sommet. 5quotesdbs_dbs28.pdfusesText_34

[PDF] arctan(a+b)

[PDF] spectre continu

[PDF] la terre est éclairée par le soleil dont la température externe

[PDF] rigel température de surface

[PDF] ardèche rivière

[PDF] ardeche vallon pont d'arc

[PDF] ardeche tourisme

[PDF] departement 08

[PDF] type de roche ardeche

[PDF] guide ardeche

[PDF] aubenas

[PDF] carte touristique ardeche

[PDF] meteo ardeche

[PDF] exemple d'application arduino

[PDF] exemple d'application arduino pdf