 Différences entre Arrangements Permutations et Combinaisons
Différences entre Arrangements Permutations et Combinaisons
7 oct. 2021 En utilisant notre formule cela nous fait n!=3!=3 × 2=6 permutations. Arrangement. Un arrangement (sans répétition) sur un ensemble est le ...
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
Un restaurant propose sur sa carte 3 entrées 4 plats de résistance et 2 desserts. Pour résumer : Arrangement
 Dénombrement
Dénombrement
arrangements. Remarque : On retiendra que l'on utilise les combinaisons dans les problèmes de choix simultanés de p éléments choisis.
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Définition : Un combinaison de k éléments pris dans un ensemble `a n éléments ... Combien y a-t-il de répartitions possibles des cartes entre ces ...
 Adimaker Théorie des ensembles
Adimaker Théorie des ensembles
La différence entre un arrangement de k éléments de E et une combinaison de k éléments de E est la suivante : dans l'arrangement les éléments sont ordonnés
 Un certain regard sur le dénombrement et la loi binomiale
Un certain regard sur le dénombrement et la loi binomiale
combinaisons ? La différence fondamentale entre un arrangement et une combinaison est l'ordre. Les 3-combinaisons aef et eaf sont la même 3-combinaison.
 Sans titre
Sans titre
La différence entre arrangements et combinaisons correspond au fait que dans les combi- naisons on ne s'intéresse pas à l'ordre des éléments. Cette fois
 listes 2 Tirages successifs sans remise : arrangements
listes 2 Tirages successifs sans remise : arrangements
L'urne est celle du § 1.2. un exemple d'arrangement de 5 éléments choisis parmi 8 est 25347. Le résultat de ce tirage simultané est une combinaison de p ...
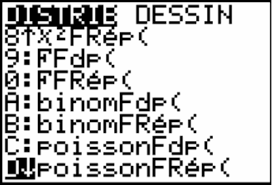 Usage des calculatrices de type TI-82 stats et TI-83+ 1 Calcul de la
Usage des calculatrices de type TI-82 stats et TI-83+ 1 Calcul de la
On l'obtient en tapant successivement : 10 MATH (sedéplaceràdroitedel'écran) PRB 3 (Combinaison)puistaperle3final. 2) sur 10 essais par exemple on entre dans ...
 1 Arrangements nombre Ap 2 Combinaisons
1 Arrangements nombre Ap 2 Combinaisons
https://imag.umontpellier.fr/~lleras/AnpCnp.pdf
 [PDF] COMBINATOIRE ET DÉNOMBREMENT - maths et tiques
[PDF] COMBINATOIRE ET DÉNOMBREMENT - maths et tiques
Elles sont au nombre de 8 et en effet : 2 = 8 Arrangement permutation combinaison : lequel choisir ? : Vidéo https://youtu be/hWkIwXXEECc
 [PDF] Analyse combinatoire
[PDF] Analyse combinatoire
6 mar 2008 · Définition : Un arrangement est une permutation de k éléments pris Notation : le nombre de combinaisons de k parmi n est noté Cnk ou
 [PDF] COMBINAISONS BINOME DE NEWTON - Pierre Lux
[PDF] COMBINAISONS BINOME DE NEWTON - Pierre Lux
Une permutation d'un ensemble E ayant n éléments est un arrangement des n éléments de E • Pour n ? 2 on appelle « factorielle n » et on note n ! le
 [PDF] Différences entre Arrangements Permutations et Combinaisons
[PDF] Différences entre Arrangements Permutations et Combinaisons
7 oct 2021 · Un arrangement (sans répétition) sur un ensemble est le nombre de possibilités de prendrek éléments dans un ensemble à n éléments (en
 [PDF] Chapitre 1 Analyse combinatoire
[PDF] Chapitre 1 Analyse combinatoire
Permutation sans répétition Définition Une permutation sans répétitions de ces n éléments est un arrangement sans répétitions de ces n éléments pris de nà
 [PDF] Comment aborder un problème de permutation arrangement et
[PDF] Comment aborder un problème de permutation arrangement et
Comment aborder un problème de permutation arrangement et combinaison Méthodes Ordre Nombre d'éléments Permutation Souvent utilisé avec AVEC
 [PDF] Dénombrement
[PDF] Dénombrement
arrangements Remarque : On retiendra que l'on utilise les combinaisons dans les problèmes de choix simultanés de p éléments choisis
 [PDF] 1Analyse Combinatoire 2Probabilités 3Variables Aléatoires 4Lois
[PDF] 1Analyse Combinatoire 2Probabilités 3Variables Aléatoires 4Lois
2 3 Arrangements sans Répétition 3 Permutations 3 1 Permutations sans Répétition 3 2 Permutations avec Répétitions 4 Combinaisons 4 1 Définition
 [PDF] Différences entre Arrangements Permutations et Combinaisons
[PDF] Différences entre Arrangements Permutations et Combinaisons
7 oct 2021 · Cet article présente les di érences entre les arrangements les permutations et les combinaisons en dénombrement illustrées de plusieurs
 [PDF] COMBINATOIRE ET DÉNOMBREMENT - maths et tiques
[PDF] COMBINATOIRE ET DÉNOMBREMENT - maths et tiques
Une combinaison de éléments de est un sous-ensemble de Propriété : Soit un ensemble à éléments Le nombre de combinaisons de éléments de
 [PDF] Analyse combinatoire
[PDF] Analyse combinatoire
6 mar 2008 · Définition : Un arrangement est une permutation de k éléments pris parmi n éléments distincts (k ? n) Les éléments sont pris sans
 [PDF] 1Analyse Combinatoire 2Probabilités 3Variables Aléatoires 4Lois
[PDF] 1Analyse Combinatoire 2Probabilités 3Variables Aléatoires 4Lois
2 2 Arrangements avec Répétitions 4 1 Définition 4 2 Combinaison sans Remise 4 3 Combinaison avec Remises 4 4 Propriétés des Combinaisons
 Fiche explicative de la leçon : Propriétés des combinaisons - Nagwa
Fiche explicative de la leçon : Propriétés des combinaisons - Nagwa
La principale différence entre une combinaison et un arrangement est que l'ordre n'a pas d'importance Pour un arrangement l'ordre est important
 Les permutations les arrangements et les combinaisons - Alloprof
Les permutations les arrangements et les combinaisons - Alloprof
Une disposition d'éléments peut être ordonnée pour tous les éléments (permutation) pour certains éléments (arrangement) ou non ordonnée (combinaison)
 Arrangement permutation combinaison : lequel choisir - YouTube
Arrangement permutation combinaison : lequel choisir - YouTube
6 oct 2020 · Dans cette vidéo tu pourras apprendre à utiliser les bons outils de dénombrement : nombre de p Durée : 18:18Postée : 6 oct 2020
 [PDF] Dénombrement
[PDF] Dénombrement
Soit E un ensemble à n éléments Un n-arrangement de E est appelé une permutation de E Une permutation est donc un n-uplet constitué dans un certain ordre
 [PDF] Combinatoire et dénombrement (II)
[PDF] Combinatoire et dénombrement (II)
? Un arrangement de k éléments de E est un k-uplet SANS répétition Par exemple (1;2) et (2;1) sont deux arrangements distincts ? Une combinaison de
Quel est la différence entre arrangement et combinaison ?
Une combinaison est une sélection de �� éléments choisis sans répétition parmi un ensemble de �� éléments pour laquelle l'ordre n'a pas d'importance. La principale différence entre une combinaison et un arrangement est que l'ordre n'a pas d'importance. Pour un arrangement, l'ordre est important.Comment reconnaître un arrangement ?
Les arrangements d'un ensemble se distinguent par l'ordre des éléments qui les composent. Par exemple, (A,C) et (C,A) sont 2 arrangements différents de l'ensemble {A,B,C}.Quand on utilise l'arrangement ?
La notion d'arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. et vaut : Akn est en fait le nombre d'injections que l'on peut faire d'un ensemble. à k éléments vers un ensemble à n éléments.- · Une permutation est donc un arrangement complet: de toutes les cartes parmi toutes les cartes. · Avec un arrangement, il y a (n – p) fois moins de cas que pour une permutation.
![[PDF] Combinatoire et dénombrement (II) [PDF] Combinatoire et dénombrement (II)](https://pdfprof.com/Listes/17/13557-17CombinatoireII.pdf.pdf.jpg)
Combinatoire et dénombrement (II)
I. Le compte est-il bon ?
1. Le scrabble...
a. Écrire tous les mots de deux lettres, ayant un sens ou pas, avec ces quatre lettres.b. Combien peut-on créer de mots de trois lettres, ayant un sens ou pas, avec ces quatre lettres ?
2. La marguerite...Chaque pétale peut être coloriée en rouge, en bleu ou en jaune.
Combien de fleurs différentes peut-on créer ?3. Les poignées de mains...
Sept amis se retrouvent et chacun salue l'autre d'une poignée de main. Combien de poignées de main échangées au total ?4. Le podium...
10 athlètes courent la finale du 100 m.
Combien de classements possibles sur le podium ?
5. La surprise...
Une surprise comprend 5 bonbons, tous de couleur différente. a. On pioche 2 bonbons au hasard en tenant compte de l'ordre : combien il-y-a-t-il de tirages possible ? b. Même question si cette fois sans tenir compte de l'ordre.Lycée S. Hessel - valérie Larose1/6
II - Les arrangements
On parle d'arrangement lorsqu'on fabrique un p-uplet (donc on tient compte de l'ordre) sans répétition.
Exemple 1 : Dans le cas du podium, l'ordre a de l'importance (les médailles n'ont pas la même couleur) et
il n'y a pas de répétition (chaque médaille n'est attribuée qu'une seule fois).Dans le cas du scrabble, l'ordre a de l'importance (pour que le mot ait un sens, l'ordre des lettres compte)
et il n'y a pas de répétition (chaque lettre n'est utilisée qu'une seule fois).Contre exemple : dans le cas de la marguerite, on choisit une couleur par pétale mais il y a des répétitions
donc ce n'est pas un 6-uplet. n et p sont deux entiers naturels avec p⩽n. E est un ensemble à n éléments.Définition : Un arrangement dep éléments d'un ensemble E de cardinaln est un p-uplet d'éléments
distincts de E. On note Anp le nombre d'arrangements de p éléments d'un ensemble E de cardinal n.Propriété : Anp=n×
(n-1)×(n-2)×...×(n-p+1)n possibilité pour le 1er choix, (n-1) pour le second, ... (n-p+1) pour le dernier choix.Ainsi pour le podium, on a 10 possibilités pour la médaille d'or, 9 pour celle d'argent et 8 pour celle de
bronze soit 10×9×8=720 possibilités : A103=10× (10-1)×(10-2).Pour le scrabble, on a 4 possibilités pour la 1ère lettre, 3 pour la seconde et 2 pour la dernière soit
4×3×2=12 possibilités : A43=4×(4-1)×(4-2).
Définition et notation : on appelle factorielle n, et on note n! le produit de tous les entiers de 1 à n.
n!=n×(n-1)×(n-2)×...×1 - Par convention 0!=1.Propriété : Anp=n×
(n-1)×(n-2)×...×(n-p+1)=n!(n-p)!preuve n°1Cas particulier : permutation
Définition : Dans le cas où
p=n, un arrangement des n éléments d'un ensemble E est une permutation. Propriété : Le nombre de permutations de E est Ann=n!Exercice n°1 : Un tournoi de tennis concerne 12 joueurs. Le palmarès récompense le gagnant du tournoi
ainsi que les 2e, 3e, 4e et 5e joueur. Combien de palmarès différents peut-il exister ? Exercice n°2 : Jules range sur une même étagère 5 romans, 3 polars et 2 BD. a. Combien existe-t-il de façons différentes de ranger ces 10 livres ? b. Même question si maintenant les livres sont rangés par catégorie. Exercice n°3 : calculer n! pour n de 1 à 10. Vérifier votre calcul avec la calculatrice.Lycée S. Hessel - valérie Larose2/6
III - Combinaisons
1. Activité
On dispose de 7 jetons numérotés de 1 à 7. L'objectif est de déterminerle nombre C de façons différentes
de choisir 4 jetons parmi les 7. Pour cela, on imagine une boîte de rangement à 4 cases.a. Déterminer le nombre de façons différentes de remplir les 4 cases en mettant un jeton dans chaque
case, l'un après l'autre, de gauche à droite (autrement dit, déterminer le nombre de 4-uplets possibles sans
répétition).b. Maintenant on choisit 4 jetons parmi les 7, par exemple 5 ; 7 ; 2 ; 1 (il y a C façons de le faire).
b1. Déterminer le nombre de façons de ranger ces 4 jetons 5 ; 7 ; 2 ; 1 dans le casier. b2. Exprimer en fonction de C le nombre total de façons de choisir 4 jetons puis de les ranger. b3. En déduire C.2. Combinaison de p éléments
n et p sont deux entiers naturels avec p⩽n. E est un ensemble à n éléments.Définition : Une combinaison de p éléments de E est un sous-ensemble (une partie) de E possédant p
éléments.
Exemple 2 : E est l'ensemble des 7 jetons de l'activité ci-dessus. L'ensemble {1 ; 2 ; 5 ; 7} est une combinaison de 4 éléments de E. L'ensemble {2 ; 4; 6} est une combinaison de 3 éléments de E.Notation et propriété
Le nombre de combinaisons de p éléments de E, noté (n p), est (n p)=Anp p!=n! p!(n-p)! (n p) est appelé coefficient binomial et se lit p parmi n. Si p>n, (n p)=0 par convention.Une autre notation existe : Cnp Exercice 4 : E = {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9} ABCDLe nombre de sous-ensembles
de E à 3 éléments est : (103)10!92310Le nombre de combinaisons
de 5 éléments de E est :10! 5! (105)105252
(23 5)=(523)(18
5)(2318)23×5Exercice 5 : On dispose d'un jeu de 32 cartes. Combien de façons différentes existe-t-il de choisir :
a. 6 cartes parmi les 32 ?b. 4 cartes parmi les trèfles ?c. 3 coeurs et 2 piques ? d. Le valet de coeur et 4 autres cartes.Exercice 6 : Remplir une grille de Loto consiste à choisir 5 numéros entre 1 et 49 (l'ordre ne compte pas)
puis un numéro " chance » de 1 à 10. a. Combien de grilles différentes peut-on remplir ? b. Parmi ces grilles, combien seront composées uniquement de numéro pairs ?Lycée S. Hessel - valérie Larose3/6
Avec une calculatrice :
ATTENTION, on ne confond pas arrangement, combinaison et k-upletSoit E={1 ; 2 ; 3}
Voici toutes les parties de E : ∅={} ; {1} ; {2} ; {3} ; {1 ; 2} ; {1 ; 3} ; {2 ; 3} ; {1 ; 2 ; 3}. Il y en a 8.
► Un arrangement de k éléments de E est un k-uplet SANS répétition. Par exemple (1;2) et (2;1) sont deux arrangements distincts. ► Une combinaison de partie de E. Par exemple {1;2} est une combinaison de 2 éléments de E ; c'est la même que {2;1}.►Un k-uplet est une liste ORDONNÉE de k éléments de E, éventuellement deux fois le même.
Par exemple (2;2) est un 2-uplet de E.
(1,2) et (2,1) sont deux 2-uplets différents.SANS ORDREORDONNÉ
SANS RÉPÉTITIONCombinaison
Exemple : le lotoArrangements
Exemple : le podium
AVEC RÉPÉTITIONS
POSSIBLESk-uplets
Exemple : le code secret à k chiffres
MéthodeOrdreNombre d'éléments
PERMUTATIONToujours AVEC ordreTous les éléments (n) ARRANGEMENTToujours AVEC ordreConcerne un sous-ensemble d'éléments (p). COMBINAISONSANS ordreConcerne un sous-ensemble d'éléments (p). Exemple : Il y a 8 athlètes qui participent aux 100 m.Combien pouvons-nous obtenir de
classements finaux ? Combien pouvons-nous obtenir de podiums ? De combien de façons possibles pouvons-nous choisir 4 athlètes dans le but de les convoquer à une réunion ? a) Est-ce que l'ordre est important? OUI b) Est-ce que cela concerne tous les éléments? OUI a) Est-ce que l'ordre est important? OUI b) Est-ce que cela concerne tous les éléments? NON a) Est-ce que l'ordre est important? NON b) Est-ce que cela concerne tous leséléments? NON
Donc, c'est une permutation
n!=8!=40320Donc, c'est un arrangement n=8 et p=3 A83=8×7×6=336Donc, c'est une combinaison
n=8 et p =3 (8 4)=70Lycée S. Hessel - valérie Larose4/6
IV - Calculer avec les coefficients binomiaux
Si p=0, alors (n
0)=1 car le seul sous-ensemble de E ayant 0 éléments est l'ensemble vide ∅
Si p=1 alors (n1)=n car il y a n sous-ensemble de E à 1 élément ( n singletons).
Si p=n alors
(n n)=1 car il y a un seul sous-ensemble de E à n élément : E.quotesdbs_dbs2.pdfusesText_2[PDF] arrangement combinaison permutation exercices corrigés
[PDF] methode arraylist java
[PDF] arraylist string java
[PDF] arraylist java example
[PDF] arraylist java open classroom
[PDF] exemple arraylist java
[PDF] créer une arraylist java
[PDF] constructeur arraylist java
[PDF] arraylist<int>
[PDF] droit d'arrestation article
[PDF] interpellation police a domicile
[PDF] arrestation enquête préliminaire
[PDF] arrestation procédure pénale
[PDF] heure légale arrestation
