 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
Limites usuelles lnx x. −−−−−→ x→+∞. 0 x lnx −−−−−→ x→0+. 0 ln(x) x sin(f (x)) ∼ x→a f (x) tan(f (x)) ∼ x→a f (x) cos(f (x))−1 ∼ x→a ...
 Feuille dexercices 10 Développements limités-Calculs de limites
Feuille dexercices 10 Développements limités-Calculs de limites
(3 )4. 4! ne sert à rien puisque le développement limité de sin(2 ) commence par 2 . ) + cos( )sin(. . 4. ) = √2. 2 sin( ) +. √2. 2 cos( ). = √2. 2.
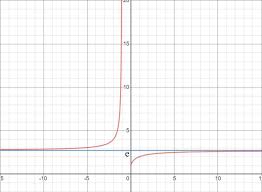 1. Limites
1. Limites
et cos(–x) = cos(x). Comme la limite à gauche est égale à la limite à droite sin(x)=sin( π. 3 )= √3. 2. Limite du quotient de deux fonctions. 1er cas ...
 Limites et dérivées de fonctions trigonométriques
Limites et dérivées de fonctions trigonométriques
Question 2. Évaluer et simplifier les expressions suivantes. a) sin. (π. 2. ) b) cos. (7π.
 I) Développements limités usuels
I) Développements limités usuels
I) Développements limités usuels. Tous les DL usuels suivants sont au (cos(x) = (eix)) sin(x) = x. − x3. 3! + ... + (−1)n x2n+1. (2n + 1)!. + o(x2n+ ...
 Tableaux des dérivées
Tableaux des dérivées
%20primitives
 Les Développements Limités
Les Développements Limités
Exemple. Calculons le DL de la fonction f(x) = sin x/ cos x à l'ordre 3 au point 0. Comme
 Limites usuelles fonctions trigonométriques pdf
Limites usuelles fonctions trigonométriques pdf
(sin) cosinus (En mathématiques les fonctions trigonométriques sont des fonctions d'angle importantes pour) (cos) tangente (tg = sin/cos) (notée aussi ...
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Les fonctions sinus et cosinus - Lycée dAdultes
Les fonctions sinus et cosinus - Lycée dAdultes
26 juin 2013 3.2 Application aux calculs de limites . ... sin′ x = cos x et cos′ x = − sin x. Remarque : On admettra ces ...
 Les fonctions sinus et cosinus - Lycée dAdultes
Les fonctions sinus et cosinus - Lycée dAdultes
26 juin 2013 3.2 Application aux calculs de limites . ... Remarque : ?x ? R ? 1 ? sin x ? 1 et ? 1 ? cos x ? 1. 2.2 Propriétés. 2.2.1 Parité.
 FONCTIONS USUELLES
FONCTIONS USUELLES
u Un certain nombre de limites usuelles doivent être connues : cos(x) = eix + e–ix. 2 sin(x) = eix – e–ix. 2i tan(x) = sin(x) cos(x).
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? cos(f (x))?1 ? x?a? (.
 Développements limités
Développements limités
4. exp(sin(x)) à l'ordre 4. 5. sin6(x) à l'ordre 9. 6. ln(cos(x)) à l'ordre 6. 7. 1 cosx à l'ordre 4. 8. tanx à l'ordre 5 (ou 7 pour les plus courageux).
 Les Développements Limités
Les Développements Limités
Calculons le DL de la fonction f(x) = cos x. sin x à l'ordre 5 au point 0.Ona: sin x = x ? x3. 6.
 DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
DEVELOPPEMENTS LIMITÉS USUELS. Le développement limité de MAC LAURIN au voisinage de x = 0 à l'ordre "n" pour une fonction "f" indéfiniment dérivable
 Feuille dexercices 10 Développements limités-Calculs de limites
Feuille dexercices 10 Développements limités-Calculs de limites
avec cos(0) = 1 ? 0 donc il suffit de déterminer les développements limités de sin( ) et de cos( ) à l'ordre 5 en 0. la division suivant les puissances
 fonctions-usuelles.pdf
fonctions-usuelles.pdf
f(x)=cos(x) g(x)=sin(x) h(x)=tan(x)??. Page 3. D'autres fonctions usuelles a) Réciproques des fonctions limite en +? de p(x)= limite en +? de x24.
 Recherche de la limite lorsque x tend vers 0 de la fonction f(x) =
Recherche de la limite lorsque x tend vers 0 de la fonction f(x) =
Limite de sinx / x. 5. L'aire du triangle OAD est (cos . sin )/2 ; celle du secteur OAC est /2 et enfin l'aire du triangle OBC est (1 . tan )/2.
 Développements limités
Développements limités
Nous verrons que toutes les fonctions usuelles admettent un développement limité Partez avec les développements limités de sin et cos à l'ordre 5 :.

DERNIÈRE IMPRESSION LE26 juin 2013 à 15:06
Les fonctions sinus et cosinus
Table des matières
1 Rappels2
1.1 Mesure principale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Résolution d"équations. . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.3 Signe des lignes trigonométriques. . . . . . . . . . . . . . . . . . . 3
2 Fonctions sinus et cosinus3
2.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2 Propriétés. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2.1 Parité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2.2 Périodicité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.3 De sinus à cosinus. . . . . . . . . . . . . . . . . . . . . . . . 4
3 Étude des fonctions sinus et cosinus4
3.1 Dérivées. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.2 Application aux calculs de limites. . . . . . . . . . . . . . . . . . . . 5
3.3 Variation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.4 Courbes représentatives. . . . . . . . . . . . . . . . . . . . . . . . . 6
3.5 Compléments. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
4 Application aux ondes progressives6
4.1 Onde sonore. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
4.2 Harmoniques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
PAULMILAN1 TERMINALES
1 RAPPELS
1 Rappels
1.1 Mesure principale
Définition 1 :On appelle mesure principale d"un angleα, la mesurexqui se trouve dans l"intervalle]-π;π] Exemple :Trouver la mesure principale des angles dont les mesures sont :17π
4et-31π6
17π4estunmesuretropgrande(>π),ilfautdoncluienleveruncertainnombre
kde tours (2π) pour obtenir la mesure principale :17π
4-k2π=π(17-8k)4=π4aveck=2
-31π6est une mesure trop petite(?-π), il faut donc lui rajouter un certain nombrekde tours (2π) pour obtenir la mesure princimale :31π
6+k2π=π(-31+12k)6=5π6aveck=3
1.2 Résolution d"équations
Théorème 1 :Équations trigonométriques L"équation cosx=cosaadmet les solutions suivantes surR: x=a+k2πoux=-a+k2πaveck?Z L"équation sinx=sinaadmet les solutions suivantes surR: x=a+k2πoux=π-a+k2πaveck?Z Exemple :Résoudre dansRles équations suivantes : a)⎷2cosx-1=0 b) 2sinx-⎷3=0
a)⎷2cosx-1=0?cosx=1⎷2?cosx=cosπ4On obtient les solutions :x=π
4+k2πoux=-π4+k2πaveck?Z
b) 2sinx-⎷3=0?sinx=⎷3
2?sinx=sinπ3
On obtient les solutions :
x=π3+k2πoux=π-π3+k2π=2π3+k2πaveck?Z
PAULMILAN2 TERMINALES
1.3 SIGNE DES LIGNES TRIGONOMÉTRIQUES
1.3 Signe des lignes trigonométriques
Théorème 2 :On a sur]-π;π],
sinx>0?x?]0 ;π[ cosx>0?x??2;π2?
O0π
2 2π sinx>0 cosx>02 Fonctions sinus et cosinus
2.1 Définition
Définition 2 :À tout réelx, on as-
socie un point unique M du cercle unité ou cercle trigonométrique de centre O, dont les coordonnées sont :M(cosx; sinx)
sinx cosx xM O Définition 3 :On appelle fonctions sinus et cosinus les fonctions respectives : x?→sinxetx?→cosxRemarque :?x?R-1?sinx?1 et-1?cosx?1
2.2 Propriétés
2.2.1 Parité
Théorème 3 :D"après les formules de trigonométrie, La fonction sinus est impaire :?x?Rsin(-x) =-sinx La fonction cosinus est paire :?x?Rcos(-x) =cosx ConséquenceLa courbe représentative de la fonction sinus est symétrique par rapport à l"origine, et la courbe représentative de la fonction cosinus est symé- trique par rapport à l"axe des ordonnées.PAULMILAN3 TERMINALES
3 ÉTUDE DES FONCTIONS SINUS ET COSINUS
2.2.2 Périodicité
Théorème 4 :D"après la définition des lignes trigonométriques dans le cercle, les fonctions sinus et cosinus sont 2πpériodiques :T=2π ?x?Rsin(x+2π) =sinxet cos(x+2π) =cosx ConséquenceOn étudiera les fonctions sinus et cosinus sur un intervalle de 2π, par exemple]-π;π].2.2.3 De sinus à cosinus
Théorème 5 :D"après les formules de trigonométrie, on a : sin 2-x? =cosxet cos?π2-x? =sinx Exemple :Résoudre dans l"intervalle]-π;π], l"équation suivante : sin x+π 4? =cosx On transforme par exemple le cosinus en sinus, l"équation devientalors : sin? x+π 4? =sin?π2-x? DansR, on trouve les solutions suivantes :x+π4=π2-x+k2π
x+π4=π-?π2-x?
+k2π?2x=π4+k2π
0x=π-π
2-π4+k2π
La deuxième série de solutions étant impossible, on trouve alors dansR x=π8+kπ
Dans l"intervalle]-π;π], on prendk=-1 etk=0 , soit les solutions x=-7π8oux=π8
3 Étude des fonctions sinus et cosinus
3.1 Dérivées
Théorème 6 :Les fonctions sinus et cosinus sont dérivables surR: sin ?x=cosxet cos?x=-sinxRemarque :On admettra ces résultats.
PAULMILAN4 TERMINALES
3.2 APPLICATION AUX CALCULS DE LIMITES
Exemple :Déterminer la dérivée de la fonction suivante : f(x) =cos2x+cos2x La fonctionfest dérivable surRcar composée et produit de fonctions dérivables surR f ?(x) =-2sin2x-2sinxcosx =-2sin2x-sin2x =-3sin2x3.2 Application aux calculs de limites
Théorème 7 :D"après les fonctions dérivées des fonctions sinus et cosinus, on a : limx→0sinx x=1 et limx→0cosx-1x=0 ROCDémonstration :On revient à la définition du nombre dérivée en 0. sin ?0=limx→0sinh-sin0 h=limh→0sinhh or on sait que : sinquotesdbs_dbs2.pdfusesText_2[PDF] Les limites:Les limites limites
[PDF] les lions du cratère ngorongoro svt correction
[PDF] les lipides biochimie pdf
[PDF] les lipides dans l'organisme
[PDF] les lipides pdf
[PDF] les liquides et la conduction électrique
[PDF] Les lithosphères
[PDF] les littoraux espaces convoités conclusion
[PDF] les littoraux espaces convoités croquis
[PDF] les littoraux espaces convoités etude de cas
[PDF] les littoraux espaces convoités problématique
[PDF] les littoraux espaces convoités seconde
[PDF] Les littoraux exposé
[PDF] les livres gratuits pdf
