 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
1 + tan2( ). = 2sin( ) cos( ). × cos2( ) = 2sin( )cos( ) = sin(2 ). 3. sin(2arctan(. 1. 3. )) = 2tan(arctan (. 1. 3)).
 350 exercices corrigés dAnalyse
350 exercices corrigés dAnalyse
√1. − x2. . ∀x ∈] − 1
 Feuille dexercices du cours dAnalyse 2 DUMI2E — Premi`ere année
Feuille dexercices du cours dAnalyse 2 DUMI2E — Premi`ere année
Exercice 6 Calculer le DL d'ordre 5 de la fonction log(1 + sinx) au voisinage du point x = 0. Exercice 7 Soit g la fonction x → arctan x. (sin x)3. −. 1 x2.
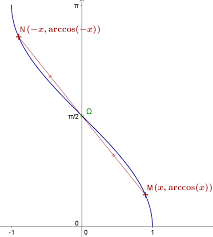 Corrigés des exercices 7 Applications & Fonctions circulaires
Corrigés des exercices 7 Applications & Fonctions circulaires
Cf cours : on peut procéder comme précédemment (via une étude de fonction) ou utiliser la concavité de arctan sur R+. Exercice 6. Simplifier les expressions
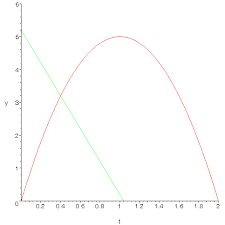 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
Exercices corrigés Fonctions b. 2. 2. ( ) sin cos sin La courbe γ est la courbe représentative d'une fonction appelée arc tangente notée arctan (tan−1 sur.
 Walanta
Walanta
Daniel Alibert – Cours et Exercices corrigés – Volume 5. 18. ˘ tangente et arctangente. La fonction arctan (ou arctg) est définie sur R: arctan : R →. −π. 2.
 Fonctions circulaires et hyperboliques inverses
Fonctions circulaires et hyperboliques inverses
Exercice 1. Vérifier arcsinx+arccosx = π. 2 et arctanx+arctan. 1 x. = sgn(x) π. 2 . Indication ▽. Correction ▽. Vidéo □. [000752]. Exercice 2. Une
 2 Fonctions trigonométriques
2 Fonctions trigonométriques
(c) Même questions pour les fonctions cosinus et arccosinus. (d) Même questions pour les fonctions tangente et arctangente. Exercice 2.4. Calculez arcsin(. √.
 Exercices sur les fonctions trigonométriques réciproques
Exercices sur les fonctions trigonométriques réciproques
19 Calculer la dérivée de la fonction f : x. Arctan(Arctan x). 20 Donner une Il faut reprendre le corrigé avec l'énoncé modifié.. 16 cos sin. 65.
 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
Correction exercice 1. Car arctan est strictement croissante donc. 0 < arctan ( ... Sur quel ensemble cette fonction est-elle définie et continue ?
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Exercice 9 ** Mines de DOUAI 1984. On considère la fonction numérique f telle que : f(x)=(x2 ?1)arctan. 1. 2x?1. et on appelle (C)
 Devoir de Mathématiques 3 : corrigé Exercice 1.Étude dune fonction
Devoir de Mathématiques 3 : corrigé Exercice 1.Étude dune fonction
Exercice 1. Dans cet exercice on étudie deux équations différentielles du second ordre. ... + et de la fonction arctan dérivable sur R) ; sa dérivée est.
 Chapitre 4 FONCTIONS USUELLES Enoncé des exercices
Chapitre 4 FONCTIONS USUELLES Enoncé des exercices
Exercice 4.10 Résoudre l'équation arccos(x) + arcsin(x2 ? x + 1) = ?. 2. Exercice 4.11 Montrer que arctan 2?2! + 2 arctan?2! = ?.
 Corrigé du Devoir Surveillé n?2
Corrigé du Devoir Surveillé n?2
Exercice 2 : Autour de la fonction Arc tangente. 1. Soit x ? R. On pose t = Arctan (x) de sorte que x = tan(t) et ??. 2 <t< ?. 2 . Il s'ensuit que.
 Fonctions élémentaires Pascal Lainé 1
Fonctions élémentaires Pascal Lainé 1
2 arctan (. 1. 3. ) Allez à : Correction exercice 27. Exercice 28. Soit la fonction définie par. ( ) = . 1. Sur quel ensemble cette fonction
 Fonctions circulaires inverses Exercice 3. Arcsin Exercice 4
Fonctions circulaires inverses Exercice 3. Arcsin Exercice 4
14 nov. 2017 Le Pascal ne dispose pas des fonctions Arcsin et Arccos. Définir Arcsinx et Arccosx à l'aide de la fonction arctan. Exercice 2.
 Fonctions circulaires et hyperboliques inverses
Fonctions circulaires et hyperboliques inverses
Corrections de Léa Blanc-Centi. 1 Fonctions circulaires inverses. Exercice 1. Vérifier arcsinx+arccosx = ?. 2 et arctanx+arctan.
 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
Exercices corrigés Fonctions 4-29 : Arctangente ... courbe ? est la courbe représentative d'une fonction appelée arc tangente notée arctan (tan?1 sur.
 Chapitre 4 Fonctions usuelles
Chapitre 4 Fonctions usuelles
6 Exercices corrigés Rappeler les dérivées des fonctions Arccos Arcsin et Arctan ainsi qu'un ... Exercice 1 - Un peu de trigonométrie hyperbolique.
 [PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
[PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
1 + tan2( ) = 2sin( ) cos( ) × cos2( ) = 2sin( )cos( ) = sin(2 ) 3 sin(2arctan( 1 3 )) = 2tan(arctan ( 1 3))
 Fonction arctan exercices corrigés - etude-generalecom
Fonction arctan exercices corrigés - etude-generalecom
11 avr 2022 · Fonction arctan exercices corrigés pdf (2ème année bac sm/ Terminale) Exercice 1 Simplifier les expressions suivantes : A = arctan2 +
 [PDF] [PDF] Exo7 - Exercices de mathématiques
[PDF] [PDF] Exo7 - Exercices de mathématiques
Exercice 9 ** Mines de DOUAI 1984 On considère la fonction numérique f telle que : f(x)=(x2 ?1)arctan 1 2x?1 et on appelle (C)
 [PDF] Chapitre 4 FONCTIONS USUELLES Enoncé des exercices
[PDF] Chapitre 4 FONCTIONS USUELLES Enoncé des exercices
Exercice 4 15 Simplifier la fonction f (x) = arccos thx + 2 arctanex 2 arctan 1 ?2 + arctan 1 2?2 = ? 2 Exercice 4 25 Résoudre arg sh (x ? 1)
 [PDF] Feuille dexercices du cours dAnalyse 2 DUMI2E — Premi`ere année
[PDF] Feuille dexercices du cours dAnalyse 2 DUMI2E — Premi`ere année
Feuille 1 de TD Fonctions trigonométriques et hyperboliques Exercice 1 1 Calculer (i) arcsin(sin(1)) (ii) arcsin(sin( 19? 5 )) (iii) arctan(tan(
 [PDF] Exercices sur les fonctions trigonométriques réciproques
[PDF] Exercices sur les fonctions trigonométriques réciproques
b) Démontrer que g est dérivable en 1 Arctan 2 b et calculer 'g b QUESTIONS DE COURS 1 Simplifier Arccos(cos x) et cos(Arccos x) 2 Démontrer
 Exercices corrigés -Fonctions usuelles : fonctions trigonométriques
Exercices corrigés -Fonctions usuelles : fonctions trigonométriques
Exercices corrigés - Fonctions usuelles : fonctions trigonométriques et des fonctions suivantes : 1 arctan(tanx) 2 arccos(cosx) 3 arcsin(sinx)
 [PDF] 2 Fonctions trigonométriques - Université de Rennes
[PDF] 2 Fonctions trigonométriques - Université de Rennes
(d) Même questions pour les fonctions tangente et arctangente Exercice 2 4 Calculez arcsin( ? 3 2 ) arcsin(? ?
 [PDF] ( ) Exercices avec solutions : LIMITE ET CONTINUITE - AlloSchool
[PDF] ( ) Exercices avec solutions : LIMITE ET CONTINUITE - AlloSchool
Exercices avec solutions : Limite et continuité Exercices d'applications et de réflexions PROF: ATMANI NAJIB 2BAC SM BIOF Exercice1 :Soit la fonction :
 [PDF] Correction exercices complémentaires TD5
[PDF] Correction exercices complémentaires TD5
6 nov 2020 · Donner le domaine de définition et calculer les fonctions suivantes : 4 x ?? arccos(cos(x)) 5 x ?? tan(arctan(x))
Comment calculer l'arc tangente ?
La règle de la fonction arc tangente de base est f(x)=arctan(x). f ( x ) = arctan ? On note aussi cette fonction f(x)=tan?1(x). f ( x ) = tan ? 1 ?- Simplifier arctan(a)+arctan(b) pour a,b?0. On a tan(arctan(a)+arctan(b))=a+b1-ab donc arctan(a)+arctan(b)=arctan(a+b1-ab)[?]. Si ab=1 alors arctan(a)+arctan(b)=?/2.
Trigonométrie hyperbolique
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours Exercice 1***ITDomaine de définition et calcul des fonctions suivantes :1.x7!sin(arcsinx),
2.x7!arcsin(sinx),
3.x7!cos(arccosx),
4.x7!arccos(cosx),
5.x7!tan(arctanx),
6.x7!arctan(tanx).
2.Calculer arctan x+arctan1x
pourxréel non nul. 3. Calculer cos (arctana)et sin(arctana)pouraréel donné. 4. Calculer ,pour aetbréels tels queab6=1, arctana+arctanben fonction de arctana+b1ab(on étudiera d"abord cos(arctana+arctanb)et on distinguera les casab<1,ab>1 eta>0,ab>1 eta<0).Rsin2x
0arcsinpt dt+Rcos2x
0arccospt dt.
1.f1(x) =arcsinxp1+x2
2.f2(x) =arccos1x21+x2
13.f3(x) =arcsinp1x2arctan
q1x1+x4.f4(x) =arctan12x2arctanxx+1+arctanx1x
12 +arctan15 +arctan182+arctan22
2+:::+arctan2n
(Utiliser l"exercice 2 4)) f(x) = (x21)arctan12x1; et on appelle(C)sa courbe représentative dans un repère orthonormé. 1.Quel est l"ensemble de définition Ddef?
2. Exprimer ,sur Dnf0g, la dérivée defsous la forme :f0(x) =2xg(x). 3. Montrer que : 8x2R;2x44x3+9x24x+1>0 et en déduire le tableau de variation deg. 4.Dresser le tableau de v ariationde f.
2. En déduire la v aleurde un=20th(20x)+21th(21x)++2nth(2nx)pournentier naturel non nul etx réel non nul donnés puis calculer la limite de(un). 1. sin (2arcsinx), 22.cos (2arccosx),
3. sin2arccosx2
4. ln (px2+1+x)+ln(px
2+1x),
5. ar gsh x212x 6. ar gch(2x21), 7. ar gth qchx1chx+1 8. ch(lnx)+sh(lnx)x 1. ch x=2, 2. arcsin (2x) =arcsinx+arcsin(xp2), 3.2 arcsinx=arcsin(2xp1x2).
Correction del"exer cice1 Narcsinxexiste si et seulement sixest dans[1;1]. Donc, sin(arcsinx)existe si et seulement sixest dans[1;1]
et pourxdans[1;1], sin(arcsinx) =x. arcsin(sinx)existe pour tout réelxmais ne vautxque sixest dansp2 ;p2 . • S"il existe un entier relatifktel quep2 +2kp6xDe plus, on ak6x2p+14
0(x) =1p1x21p1x2=0:
Doncfest constante sur[1;1]et pourxdans[1;1],f(x) =f(0) =p28x2[1;1];arccosx+arcsinx=p2
:2ème solution. Il existe un unique réelqdans[0;p]tel quex=cosq, à savoirq=arccosx. Mais alors,
arccosx+arcsinx=q+arcsin sin(p2 q) =q+p2 q=p2 (car p2 qest dans[p2 ;p22.1ère solution. Pourxréel non nul, posonsf(x) =arctanx+arctan1x
.fest impaire.fest dérivable surRet pour tout réelxnon nul,f0(x) =11+x21x211+1x
2=0.fest donc constante sur]¥;0[et sur
]0;+¥[(mais pas nécessairement surR). Donc, pourx>0,f(x) =f(1) =2arctan1=p2 , et puisquef est impaire, pourx<0,f(x) =f(x) =p2 . Donc,8x2R;arctanx+arctan1x
p2 six>0 p2 six<0=p2 sgn(x):42èmesolutionPourxréelstrictementpositifdonné, ilexisteununiqueréelqdans0;p2
telquex=tanqà savoirq=arctanx. Mais alors,
arctanx+arctan1x =q+arctan1tanq =q+arctan tan(p2 q) =q+p2 q=p2 (carqetp2 qsont éléments de0;p2 3. cos2(arctana) =11+tan2(arctana)=11+a2. De plus , arctanaest dans]p2
;p2 [et donc cos(arctana)>0. On en déduit que pour tout réela, cos(arctana) =1p1+a2puis sin(arctana) =cos(arctana)tan(arctana) =ap1+a2:8a2R;cos(arctana) =11+a2et sin(arctana) =ap1+a2:4.D"après 3),
cos(arctana+arctanb) =cos(arctana)cos(arctanb)sin(arctana)sin(arctanb) =1abp1+a2p1+b2;ce qui montre déjà , puisqueab6=1, que cos(arctana+arctanb)6=0 et donc que tan(arctana+arctanb)
existe. On a immédiatement, tan(arctana+arctanb) =a+b1ab:Maintenant, arctana+arctanbest dansp;p2
[p2 ;p2 [p2 ;p.1er cas.Siab<1 alors cos(arctana+arctanb)>0 et donc arctana+arctanbest dansp2
;p2 . Dans ce cas, arctana+arctanb=arctana+b1ab.2ème cas.Siab>1 alors cos(arctana+arctanb)<0 et donc arctana+arctanbest dansp;p2
[p2 ;p.Si de plusa>0, arctana+arctanb>p2
et donc arctana+arctanbest dansp2 ;p. Dans ce cas, arctana+arctanbpest dansp2 ;p2 et a même tangente que arctana+b1ab. Donc, arctana+ arctanb=arctana+b1ab+p. Sia<0, on trouve de même arctana+arctanb=arctana+b1abp.En résumé,
arctana+arctanb=8 >:arctan a+b1absiab<1 arctan a+b1ab+psiab>1 eta>0 arctan a+b1abpsiab>1 eta<0:Correction del"exer cice3 Nch(a+b) =chachb+shashbet ch(ab) =chachbshashb; sh(a+b) =shachb+chashbet sh(ab) =shachbshbcha th(a+b) =tha+thb1+thathbet th(ab) =thathb1thathb:5Deux démonstrations :
chachb+shashb=14 ((ea+ea)(eb+eb)+(eaea)(ebeb)) =12 (ea+b+eab) =ch(a+b): th(a+b) =sh(a+b)ch(a+b)=shachb+shbchachachb+shashb=tha+thb1+thathbaprès division du numérateur et du dénominateur par le nombre non nul chachb. En appliquant àa=b=x,
on obtient :8x2R;ch(2x) =ch2x+sh2x=2ch2x1=2sh2x+1;sh(2x) =2shxchxet th(2x) =2thx1+th2x:En additionnant entre elles les formules d"addition, on obtient les formules de linéarisation :
chachb=12 (ch(a+b)+ch(ab));shashb=12 (ch(a+b)ch(ab))et shachb=12 (sh(a+b)+sh(ab)); et en particulier ch2x=ch(2x)+12
et sh2x=ch(2x)12 :Correction del"exer cice4 NPourxréel, on posef(x) =Rsin2x0arcsinpt dt+Rcos2x
0arccospt dt.
La fonctiont7!arcsinptest continue sur[0;1]. Donc, la fonctiony7!Ry0arcsinpt dtest définie et dérivable
sur[0;1]. De plus,x7!sin2xest définie et dérivable surRà valeurs dans[0;1]. Finalement, la fonction
x7!Rsin2x0arcsinpt dtest définie et dérivable surR. De même, la fonctiont7!arccosptest continue sur[0;1].
Donc, la fonctiony7!Ry
0arccospt dtest définie et dérivable sur[0;1]. De plus, la fonctionx7!cos2xest
définie et dérivable surR, à valeurs dans[0;1]. Finalement, la fonctionx7!Rcos2x0arccospt dtest définie et
dérivable surR. Donc,fest définie et dérivable surRet, pour tout réelx, f0(x) =2sinxcosxarcsin(psin
2x)2sinxcosxarccos(pcos
2x) On note alors quefestp-pérodique et paire. Pourxélément de[0;p2 ],f0(x) =2sinxcosx(xx) =0.fest donc constante sur[0;p2 ]et pourxélément de[0;p2 ],f(x) =fp4 =R1=20arcsinpt dt+R1=2
0arccosptdt=R1=2
0p2 dt=p4 . Mais alors, par parité etp-périodicité,8x2R;Rsin2x
0arcsinpt dt+Rcos2x
0arccospt dt=p4
:Correction del"exer cice5 N1.1ère solution.Pour tout réelx,px2+1>px
2=jxjet donc1 2+1<1. Ainsif1est définie et
dérivable surR, impaire, et pour tout réelx, f 01(x) =1px
2+112 x2x(x2+1)px 2+1 1q 1x21+x2=11+x2=arctan0(x):
Donc il existe une constante réelleCtelle que pour tout réelx,f1(x) =arctanx+C.x=0 fournitC=0 et donc, 6 8x2R;arcsinxpx
2+1 =arctanx:2ème solution.Pourxréel donné, posonsq=arctanx.qest dansp2 ;p2 etx=tanq. xpx 2+1=tanqp1+tan2q=pcos
2qtanq=cosqtanq(car cosq>0)
=sinq et donc f 1(x) =arcsin(sinq) =q(carqest dansi
p2 ;p2 h =arctanx: 2.1ère solution.Pour tout réelx,1<1+21+x2=1x21+x261+2=1 (avec égalité si et seulement si
x=0).f2est donc définie et continue surR, dérivable surR. Pour tout réelxnon nul, f 02(x) =2x(1+x2)2x(1x2)(1+x2)21r
11x21+x2
2=4x1+x21p4x2=2e1+x2
oùeest le signe dex. Donc il existe une constante réelleCtelle que pour tout réel positifx,f2(x) =
2arctanx+C(y comprisx=0 puisquefest continue en 0).
x=0 fournitC=0 et donc, pour tout réel positifx,f2(x) =2arctanx. Par parité, 8x2R;arccos1x21+x2
=2arctanjxj:2ème solution.Soitx2Rpuisq=arctanx.qest dansp2 ;p2 etx=tanq. 1x21+x2=1tan2q1+tan2q=cos2q(1tan2q) =cos2qsin2q=cos(2q):
Donc f 2(x) =arccos(cos(2q)) =2qsiq20;p2
2qsiq2p2
;0=2arctanxsix>0 2arctanxsix60=2arctanjxj:
3. La fonction x7!arcsinp1x2est définie et continue sur[1;1], dérivable sur[1;1]nf0gcar pourx élément de[1;1], 1x2est élément de[0;1]et vaut 1 si et seulement sixvaut 0.1x1+xest défini et positif
si et seulement sixest dans]1;1], et nul si et seulement six=1.f3est donc définie et continue surquotesdbs_dbs11.pdfusesText_17
2+1<1. Ainsif1est définie et
dérivable surR, impaire, et pour tout réelx, f01(x) =1px
2+112 x2x(x2+1)px 2+1 1q1x21+x2=11+x2=arctan0(x):
Donc il existe une constante réelleCtelle que pour tout réelx,f1(x) =arctanx+C.x=0 fournitC=0 et donc, 68x2R;arcsinxpx
2+1 =arctanx:2ème solution.Pourxréel donné, posonsq=arctanx.qest dansp2 ;p2 etx=tanq. xpx2+1=tanqp1+tan2q=pcos
2qtanq=cosqtanq(car cosq>0)
=sinq et donc f1(x) =arcsin(sinq) =q(carqest dansi
p2 ;p2 h =arctanx:2.1ère solution.Pour tout réelx,1<1+21+x2=1x21+x261+2=1 (avec égalité si et seulement si
x=0).f2est donc définie et continue surR, dérivable surR. Pour tout réelxnon nul, f02(x) =2x(1+x2)2x(1x2)(1+x2)21r
11x21+x2
2=4x1+x21p4x2=2e1+x2
oùeest le signe dex. Donc il existe une constante réelleCtelle que pour tout réel positifx,f2(x) =
2arctanx+C(y comprisx=0 puisquefest continue en 0).
x=0 fournitC=0 et donc, pour tout réel positifx,f2(x) =2arctanx. Par parité,8x2R;arccos1x21+x2
=2arctanjxj:2ème solution.Soitx2Rpuisq=arctanx.qest dansp2 ;p2 etx=tanq.1x21+x2=1tan2q1+tan2q=cos2q(1tan2q) =cos2qsin2q=cos(2q):
Donc f2(x) =arccos(cos(2q)) =2qsiq20;p2
2qsiq2p2
;0=2arctanxsix>02arctanxsix60=2arctanjxj:
3. La fonction x7!arcsinp1x2est définie et continue sur[1;1], dérivable sur[1;1]nf0gcar pourxélément de[1;1], 1x2est élément de[0;1]et vaut 1 si et seulement sixvaut 0.1x1+xest défini et positif
si et seulement sixest dans]1;1], et nul si et seulement six=1.f3est donc définie et continue surquotesdbs_dbs11.pdfusesText_17[PDF] comment la terre d'israël fut inventée pdf
[PDF] origine des juifs d'israel
[PDF] appareil circulatoire cours
[PDF] système circulatoire
[PDF] comment la terre d'israël fut inventée
[PDF] appareil circulatoire schéma
[PDF] histoire peuple hebreu
[PDF] mozart wikipedia
[PDF] tp mps poudre blanche
[PDF] exemple programme mblock arduino
[PDF] fonction de production pdf
[PDF] projet de recherche master
[PDF] fonction cobb douglas microéconomie
[PDF] fonction de production ces
