[PDF] [PDF] Limites et comportement asymptotique Exercices corrigés - E-monsite





Previous PDF Next PDF



Limites et asymptotes

f(x) = f(a). Exemple : Si a > 0 lim x→a. √x = √a. Si P est un polynôme on dit que la droite D d'équation x = a est asymptote verticale à la courbe Cf .



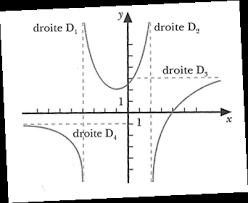Chapitre 9: Identifier la position des asymptotes dune fonction grâce Chapitre 9: Identifier la position des asymptotes dune fonction grâce

Cependant il suffisait de vérifier qu'une de ces deux limites égales 4 pour conclure la présence d'une asymptote horizontale. Page 5. Exemple 9.3. Soit la 



I Asymptote Oblique II Branches paraboliques

Exemple 1 : f : R∗ −→ R x ↦− → 2x +1+. 1 x. • Cf admet-elle une droite comme asymptote en +∞? • Justifier. Exemple 2 : f : Df −→ R x ↦− → √x2 − 1+ 



LIMITES DES FONCTIONS

( ) = −∞ la droite d'équation = est appelée asymptote verticale à la courbe de la fonction . 2) Limite à gauche



Chapitre 4 - Limites et Asymptotes

On trouve les asymptotes oblique en effectuant la division euclidienne. Exemple 3.1 Les fonctions suivantes admettent-elles une asymptote oblique ? 1. f(x) 



Les asymptotes verticales et les limites infinies

Asymptote verticale. La droite x = a est une asymptote verticale si lim x→a− f(x) = ±∞ ou lim x→a+ f(x) = ±∞. Page 4. Exemple 1 f(x) = x. (x − 1)2(x − 3).



Untitled

asymptote horizontale d'équation y = 3. il me peut y avoin qu'ume éventuelle asymptote oblique. Exemple de tableau avec valeur interdite.



5. Études de fonctions

Par exemple on a vu que sin(x) x a un trou en x = 0. Les asymptotes verticales



Limites de fonctions (3) : asymptotes horizontales asymptotes

Reconnaissance d'asymptote horizontale et d'asymptote verticale. 1°) Règle. On Faire un exemple avec x→ 4+ et x→ 4 . On change non pas de courbe mais de ...



Limites de fonctions

Pour les deux exemples précédents nous aurions pu formuler la question autrement : « déterminez l'asymptote verticale éventuelle au graphique de cette fonction 



[PDF] Identifier la position des asymptotes dune fonction grâce aux limites

Exemple 9 1 Pour savoir si une fonction possède une asymptote verticale il faut déterminer les valeurs de x qui annulent le dénominateur



[PDF] Chapitre 4 - Limites et Asymptotes - BDRP

Notes du cours donné par M Gelsomino (2005-2008) Gymnase de Burier 1 Valeurs interdites et asymptotes verticales Exemple 1 1 Etudier la fonction f(x) =



[PDF] 1ère S Cours AH et AVpdf

asymptotes horizontales asymptotes verticales 2°) Exemple La courbe admet l'axe des abscisses pour asymptote horizontale (en +? et en – ?) et 



[PDF] Asymptotes verticales et horizontales

Cette droite est donc une asymptote verticale La fonction g est un bel exemple qui nous montre que le calcul de la limite n'est pas nécessairement 



[PDF] asymptotespdf

déterminer une asymptote verticale de Cf déterminer une asymptote horizontale de Cf exemple 3 (on donne l'équation de la droite dans l'énoncé)



[PDF] Chapitre 2: Limites et Asymptotes

voisinage d'un trou ou d'un bord (point limite ou asymptote verticale) de son domaine de Exemple: En étudiant les graphiques les fonctions f ci-dessous 



[PDF] Limites et asymptotes

par exemple f définie sur R par f (x) = cos(x) n'a de limite ni en on dit que la droite D d'équation x = a est asymptote verticale à la courbe Cf



[PDF] Limites et comportement asymptotique Exercices corrigés - E-monsite

Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe (asymptote verticale et asymptote horizontale)



[PDF] Limites et asymptotes

on dit que la droite D d'équation x = a est asymptote verticale à la courbe Cf P et M sont ici les deux points de même ordonnée et la distance PM tend vers 



[PDF] Chapitre 4 - Limites et Asymptotes - BDRP

Notes du cours donné par M Gelsomino (2005-2008) Gymnase de Burier 1 Valeurs interdites et asymptotes verticales Exemple 1 1 Etudier la fonction f(x) =



[PDF] Compléments sur les limites asymptotes et continuité

27 fév 2017 · La droite ? d'équation x = a est dite asymptote verticale à Cf au point a Remarque : L'intervalle D =]b ; a[?]a ; c[ est appelé voisinage 



[PDF] Limites et comportement asymptotique Exercices corrigés - E-monsite

Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe (asymptote verticale et asymptote horizontale)



[PDF] Identifier la position des asymptotes dune fonction grâce aux limites

Exemple 9 1 Pour savoir si une fonction possède une asymptote verticale il faut déterminer les valeurs de x qui annulent le dénominateur



[PDF] LIMITES & ASYMPTOTES ( )

f(x)=± õ et/ou si lim x?a x>a f(x)=± õ Alors on dit que la droite () d'équation x=a est asymptote verticale à Cf exemples : a) f(x)=



[PDF] Asymptotes verticales et horizontales

Cette droite est appelée asymptote verticale Esquissons le graphique de la fonction pour des valeurs de x près de cette asymptote verticale d'équation



[PDF] cours-asymptotespdf

Définition 10 : La droite d'équation x = a est une asymptote verticale à droite du graphique ?f Exemple : soit la fonction f définie par y = f(x) =



[PDF] les-limites-de-fonction-et-les-asymptotespdf - CoursMathsAixfr

droite horizontale asymptote en t droite verticale asymptote en o Définition et propriété Il y a trois types différents d'asymptotes (mais en Terminale 

  • Comment trouver une asymptote verticale ?

    Pour savoir si une fonction poss? une asymptote verticale, il faut déterminer les valeurs de x qui annulent le dénominateur. donc lorsque la fonction f s?approche de 1 par la gauche,???? prend des valeurs qui tendent vers ? ?. Cela confirme aussi l'asymptote verticale en x = 1 car la condition 1 est vérifiée.

  • Comment trouver les asymptotes verticales et horizontales ?

    Une asymptote horizontale : on l'obtient en étudiant une fonction en +? et -? qui tend vers un chiffre. Une asymptote verticale : on l'obtient en étudiant la limite d'une fonction en un point précis, par exemple en 2+ et 2-.

  • Comment montrer qu'une fonction admet une asymptote verticale ?

    f est définie à droite et à gauche de -2 et les limites à droite et à gauche de f en -2 sont infinies. De même, f est définie à droite et à gauche de 3 et les limites à droite et à gauche de f en 3 sont infinies. On peut donc conclure que les droites d'équation x=-2 et x=3 sont asymptotes verticales à C_{f}.
  • On cherche la limite de y(t)/x(t) quand t tend vers t0. Si cette limite est égale à un réel a non nul, on cherche alors la limite de y(t) – ax(t) quand t tend vers t0. Si cette limite est égale à un réel b, alors la droite d'équation y = ax + b est asymptote à la courbe.
1

Sont abordés dans cette fiche :

Exercice 1 : détermination graphique e équation courbe (asymptote verticale et asymptote horizontale) Exercice 2 : étude de limites, asymptotes verticales et horizontales

Exercice 3 : étude de limites de fonctions composées, formes indéterminées, expression conjuguée,

asymptotes horizontales

Exercice 4 :

Exercice 5 :

On a tracé ci-dessous en vert , la courbe représentative dfonction . Déterminer graphiquement ,

, puis une équation de chacune des asymptotes à .

Limites et comportement asymptotique

Exercices corrigés

Exercice 1 (2 questions) Niveau : facile

0

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

2

1) Ci-dessous est tracée en vert .

Rappel :

Soient

Continuité en un point : :

-à-dire et en particulier

Continuité sur un intervalle :

Graphiquement, on lit :

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

3

Remarque Notation :

et 2)

Rappel : Asymptotes à une courbe

Asymptote horizontale :

Soit asymptote horizontale asymptote horizontale

Asymptote verticale :

Si asymptote verticale

Asymptote oblique :

Soit asymptote oblique

Graphiquement, on lit :

Donc la droite - est asymptote verticale à .

désigne la limite à gauche de en désigne la limite à droite de en

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

Limites et comportement asymptotique Exercices corrigés

© SOS DEVOIRS CORRIGES (marque déposée)

4

Par ailleurs,

Donc la droite - est asymptote verticale à

Enfin,

Donc la droite est asymptote horizontale à en et en . 0 0 tend vers - par valeurs inférieures tend vers - par valeurs supérieures

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

Limites et comportement asymptotique Exercices corrigés

© SOS DEVOIRS CORRIGES (marque déposée)

5

Déterminer les limites suivantes et .

Remarque préalable : Le verbe " déduire » signifie " partir de propositions prises pour prémisses

1) Déterminons

, par quotient, On en déduit que la courbe représentative de la fonction - admet une asymptote verticale - (représentée ci-dessous en bleu).

Exercice 2 (2 questions) Niveau : facile

0

Si -, alors :

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

6

Remarque :

Cette étude de limite aurait également permis la courbe représentative de la fonction admet une asymptote verticale - (représentée ci-dessus en bleu). Autre remarque : La courbe représentative de la fonction - admet également une asymptote horizontale (représentée ci-dessous en rose) - en et en . En effet, 0

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

Limites et comportement asymptotique Exercices corrigés

© SOS DEVOIRS CORRIGES (marque déposée)

7

2) Déterminons

Et , par quotient,

Donc la courbe représentative de la fonction

admet une asymptote verticale . Remarque : On aurait asymptote verticale à la courbe représentative de la fonction en montrant que :

Autre remarque : La courbe représentative de cette fonction admet également une asymptote horizontale

en et en . En effet, on a :

Rappel : Soient , , et .

La limite en définie par :

- est égale à la limite en du quotient de ses monômes de plus haut degré 0

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

8

3) Déterminons

, par quotient, Et

Donc, par somme,

On en déduit que la courbe représentative de la fonction - admet une asymptote verticale Remarque : On pouvait également montrer en étudiant

Autre remarque : La courbe représentative de cette fonction admet également une asymptote oblique

- au voisinage de et de . En effet,

4) Déterminons

Donc , la courbe représentative de la fonction - , admet une asymptote horizontale - au voisinage de .

Remarques :

- est une asymptote horizontale à en .

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

9

5) Déterminons

Il résulte de cette étude de limite que la courbe représentative de la fonction - asymptote horizontale -.

Remarque :

6) Déterminons

Donc la courbe représentative de la fonction -

-- pas horizontale.

Remarque : La courbe représentative de cette fonction admet en revanche deux asymptotes verticales

respective - et --.

Asymptote verticale

Asymptote verticale

Asymptote oblique

Courbe représentative de

la fonction

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

10

Déterminer la limite de chacune des fonctions suivantes puis en déduire si la courbe représentative de la

fonction admet une asymptote. Rappel : Limite d fonction composée de deux fonctions

Soit une fonction définie sur un intervalle , soit une fonction définie sur un intervalle , telle que .

La fonction définie sur telle que (ou ) est la fonction composée de la fonction suivie de la fonction . , et désignent chacun soit un réel, soit , soit . Si Et si Alors

1) Déterminons

est la composée, définie sur , de la fonction suivie de la fonction . Et

Exercice 3 (2 questions) Niveau : moyen

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

11 , par composition, Et , par composition, Donc, par différence, on aboutit à une forme indéterminée de la forme ; en effet : . Pour cela, on la multiplie par son expression conjuguée, afin de mettre en évidence la forme factorisée de ((. est dite " » de . Or, d , par somme,

Donc, par quotient,

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

12 On en déduit que la courbe représentative de la fonction admet une asymptote horizontale - au voisinage de .

2) Déterminons -(

, par composition, Par conséquent, la courbe représentative de la fonction -( (- admet une asymptote horizontale au voisinage de . Remarque : On peut également montrer que la courbe représentative de la fonction -( (- admet une - au voisinage de .

3) Déterminons

, par composition, , par composition, Donc on aboutit à une forme indéterminée :

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

13 n --. Pour cela, on la multiplie par son expression conjuguée. Et , par somme, Donc Par conséquent, la courbe représentative de la fonction -- dmet pas asymptote horizontale au voisinage de .

Rappel : Formes indéterminées

Les cas de formes indéterminées (

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

14

Soit -

1) Etudier les limites de aux bornes de son ensemble de définition. En déduire les asymptotes

éventuelles.

2) Montrer que , la courbe représentative de comme asymptote

oblique.

3) Tracer et ses asymptotes afin de contrôler les résultats obtenus aux questions précédentes.

Soit -

1) Etudions les limites de aux bornes de son ensemble de définition.

On a : , , et

Etude en :

, par composition,

Exercice 4 (4 questions) Niveau : facile

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

15 , par quotient,

Donc, par somme,

Donc , la courbe représentative de , admet pas horizontale au voisinage de

Etude en :

, par composition, , par quotient,

Donc, par somme,

Donc , la courbe représentative de , admet la droite comme asymptote verticale.

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

16

Etude en :

, par composition, , par quotient,

Donc, par somme,

Donc , la courbe représentative de , admet la droite comme asymptote verticale. (résultat déjà obtenu ci-dessus)

Etude en :

, par somme, , par composition,

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

17 , par quotient,

Donc, par somme,

Donc , la courbe représentative de , admet pas horizontale au voisinage de

2) Montrons que comme asymptote oblique.

Pour tout ,

Donc Par conséquent, la droite est asymptote oblique à au voisinage de . Remarque : On peut également montrer que la droite est asymptote oblique à au voisinage de

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

18

3) Traçons (en vert) et ses asymptotes.

-dessus, on constate que les résultats obtenus aux questions précédentes sont conformes.

Soit la fonction définie sur - par :

On note sa courbe représentative dans un repère orthonormal .

1) Déterminer les réels , et tels que, pour tout réel de ,

2) Déterminer les limites de aux bornes de . En déduire les éventuelles asymptotes à parallèles aux

axes du repère.

3) Montrer que

Soit la fonction définie sur - par :

Exercice 5 (5 questions) Niveau : moyen

0

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

19 On note sa courbe représentative dans un repère orthonormal .

1) Déterminons les réels , et tels que, pour tout réel de ,

Pour tout réel de ,

Ainsi, on doit obtenir :

Par identification des coefficients (uniques) des monômes du numérateur, on a :

Résolvons ce système :

Donc, pour tout réel de ,

2) Déterminons les limites de aux bornes de déduire les éventuelles asymptotes à

parallèles aux axes du repère. Remarque : sont les asymptotes horizontales et verticales. Une asymptote horizontale est par des abscisses ; une asymptote verticale est des ordonnées.

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

20

Etudions la limite de en :

, par quotient,

Donc, par somme,

Etudions la limite de en - et en - :

, par quotient,

Donc, par somme,

Par conséquent, -

Etudions la limite de en :

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

21
, par quotient,

Donc, par somme,

3) Montrer que

de ,

Ainsi, pour tout réel de ,

Nous avons en outre établi à la question 2) que : Donc

Par conséquent au voisinage de .

Remarque : On a de surcroît :

-à-dire que au voisinage de .

PROF: ATMANI NAJIBhttp:// abcmaths.e-monsite.com

quotesdbs_dbs11.pdfusesText_17
[PDF] asymptote pdf

[PDF] asymptote cours

[PDF] asymptote formule

[PDF] asymptote limite

[PDF] hyperbole maths 2nde corrigé

[PDF] fonction hyperbole maths

[PDF] comment déterminer une asymptote

[PDF] les asymptotes cours

[PDF] exemple asymptote oblique

[PDF] asymptote exercices

[PDF] asymptote oblique graphique

[PDF] asymptote oblique exercices

[PDF] asymptote oblique pdf

[PDF] notion d asymptote pdf

[PDF] branches infinies d une fonction