 Les fonctions sinus et cosinus - Lycée dAdultes
Les fonctions sinus et cosinus - Lycée dAdultes
26 juin 2013 3.2 Application aux calculs de limites . ... • La fonction cosinus est paire : ∀x ∈ R cos(−x) = cos x. Conséquence La courbe représentative de ...
 sh(x) = b) La fonction cosinus hyperbolique : ch(x)
sh(x) = b) La fonction cosinus hyperbolique : ch(x)
sh(x)=+∞. • Limite en −∞ : lim x→−∞ ex = 0 et lim.
 Les Développements Limités
Les Développements Limités
Calculons le DL de la fonction f(x) = sin x/ cos x à l'ordre 3 au point 0. Comme lim x→0 cos x = 0 on peut appliquer le critère précédent. On
 Les fonctions sinus et cosinus
Les fonctions sinus et cosinus
17 nov. 2017 . Limites utiles - ROC. Limites qui reviennent aux nombres dérivés en 0 : • lim x→0 sin x x. = lim x→0 sin x − sin 0 x − 0. = sin′(0) = cos( ...
 Feuille dexercices 10 Développements limités-Calculs de limites
Feuille dexercices 10 Développements limités-Calculs de limites
est un développement limité dont le premier terme non nul est . 4. il suffit de faire un développement limité de 1 − cos( ) + ln(cos( )) à l'ordre 4
 Développements limités
Développements limités
−. 1. 4 x4 + o(x7). Remarque : ici il est suffisant de prendre des DL de cos et ch d'ordre 5 : cos x - 1
 LIMITES DES FONCTIONS – Chapitre 2/2
LIMITES DES FONCTIONS – Chapitre 2/2
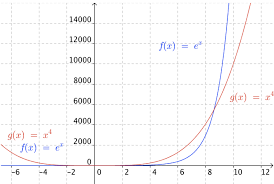
cos( ). 2+1. = 0. Partie 3 : Cas de la fonction exponentielle. 1) Limites aux bornes. Propriétés : lim. → E. = +∞ et lim. → E. = 0. Démonstration
 REVISION DEVELOPPEMENTS LIMITES LUNDI 5 JANVIER 2004
REVISION DEVELOPPEMENTS LIMITES LUNDI 5 JANVIER 2004
5 janv. 2004 ... petit des deux avant de les sommer. Application : Ecrire le développement limité de cos(x) + isin(x) `a l'ordre 5 : cos(x) + isin(x)= ...
 DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
Le développement limité de MAC LAURIN au voisinage de x = 0 à l'ordre "n" pour une fonction "f" indéfiniment dérivable s'écrit : /(x) = /(0) + x/'(0) +x2.
 Les fonctions sinus et cosinus - Lycée dAdultes
Les fonctions sinus et cosinus - Lycée dAdultes
26 jui. 2013 3 Étude des fonctions sinus et cosinus. 4. 3.1 Dérivées . ... 3.2 Application aux calculs de limites .
 sh(x) = b) La fonction cosinus hyperbolique : ch(x)
sh(x) = b) La fonction cosinus hyperbolique : ch(x)
donc par somme de limites
 Développements limités
Développements limités
La figure 3 représente les fonctions sinus et cosinus avec leurs premiers polynômes Partez avec les développements limités de sin et cos à l'ordre 5 :.
 Recherche de la limite lorsque x tend vers 0 de la fonction f(x) =
Recherche de la limite lorsque x tend vers 0 de la fonction f(x) =
Limite de sinx / x. 5. L'aire du triangle OAD est (cos . sin )/2 ; celle du secteur OAC est /2 et enfin l'aire du triangle OBC est (1 . tan )/2.
 Les fonctions sinus et cosinus
Les fonctions sinus et cosinus
17 nov. 2017 La fonction cos est paire : ?x ? R cos(?x) = cos x. Ccos admet l'axe des ordonnées pour axe de symé- trie. Limites utiles - ROC.
 Formule de Taylor développements limités
Formule de Taylor développements limités
http://www.gm.univ-montp2.fr/spip/IMG/pdf/mathsTD4.pdf
 Les Développements Limités
Les Développements Limités
Calculons le DL de la fonction f(x) = cos x. sin x à l'ordre 5 au point 0.Ona: sin x = x ? x3. 6.
 DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
DEVELOPPEMENTS LIMITÉS USUELS Le développement limité de
Le développement limité de MAC LAURIN au voisinage de x = 0 à l'ordre "n" pour une fonction "f" indéfiniment dérivable s'écrit : /(x) = /(0) + x/'(0) +x2.
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? cos(f (x))?1 ? x?a? (.
 Feuille dexercices 10 Développements limités-Calculs de limites
Feuille dexercices 10 Développements limités-Calculs de limites
avec cos(0) = 1 ? 0 donc il suffit de déterminer les développements limités de sin( ) et de cos( ) à l'ordre 5 en 0. la division suivant les puissances
Devoir à la maison n°4. TS
Limites remarquables de sinus et cosinus.Partie A. Calcul d'aire.Soit x un réel de l'intervalle ]0 ;
2 [,et M un point du cercle trigonométrique tel que la
mesure en radians de l'angleOI;OMsoit égale à x. Les éléments géométriques utilisés par la
suite sont décrits dans la figure ci-dessous. x1 Exprimer, en fonction de x, les longueurs OC, CM et IT.2 Exprimer, en fonction de x, les aires des triangles MOI et TOI.
3 Exprimer, en fonction de x, l'aire du secteur circulaire MOI.
Page 1 de 2
0I J 0 M C S TDevoir à la maison n°4. TS
4 Déduire des questions précédentes que pour tout x∈]0 ;
2 [ :sinxxtanx.Partie B. Deux limites remarquables.On admettra que les fonctions sinus et cosinus sont continues sur
ℝ.1 Déduire de la question A. 4 que pour tout x∈]0 ; 2 [ : cosxsinx x12 En déduire la limite en 0 par valeurs supérieures de sinx x3 Démontrer que la fonction f : x∈ℝ*sinx xest paire.En déduire la limite en 0 de sinx x4 Démontrer que pour tout x∈]-2 ; 0 [∪]0 ;
2 [: 11 cosxsinx
x2 =1 -cosx x25 En déduire la limite en 0 de1 -cosx
x2puis de cosx-1 x6 En déduire le nombre dérivé de sinus et de cosinus en 0.Quelques rappels. Pour x∈[0 ;2 ],la mesure en radians d'un angle est la longueur de l'arc du cercletrigonométrique.L'aire d'un secteur circulaire est proportionnelle à son angle (pour un même disque).Revoir les propriétés des inégalités et inéquations. ( cours de seconde sur le site ).Page 2 de 2
quotesdbs_dbs5.pdfusesText_10[PDF] Limites d'une fonction rationnelle en x=a
[PDF] Limites d'une suite par unicité de la limite
[PDF] limites d'une étude quantitative
[PDF] limites d'une étude scientifique
[PDF] Limites de fonction
[PDF] Limites de fonction à calculer
[PDF] Limites de fonctions
[PDF] Limites de fonctions (Terminale)
[PDF] Limites de fonctions - Reconnaître des courbes (problème pour trouver l'extremum)
[PDF] Limites de fonctions - reconnaître des courbes - (problème pour trouver l'extremum)
[PDF] limites de fonctions cours
[PDF] limites de fonctions exercices corrigés
[PDF] limites de fonctions formes indeterminées
[PDF] limites de fonctions rationnelles exercices
