 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
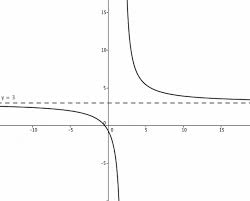
Calculer la limite de la fonction en +∞. Correction. On a : lim. →. 1. . = 0
 Limites de fonctions
Limites de fonctions
Les théorèmes suivants sont très pratiques pour calculer une limite d'une fonction compliquée en la comparant à des fonctions plus simples dont on connaît la
 Les Développements Limités
Les Développements Limités
cela d'après ce qui précède
 Limites de fonctions
Limites de fonctions
Ce qui exprime bien que la limite de f en +∞ est l. Correction de l'exercice 2 △. Généralement pour calculer des limites faisant intervenir des sommes de
 Chapitre 3 Dérivabilité des fonctions réelles
Chapitre 3 Dérivabilité des fonctions réelles
théorie notamment en utilisant la dérivée pour calculer une limite dans le cas de formes On voudrait `a présent calculer les dérivées des fonctions usuelles.
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
Déterminer les limites des fonctions suivantes aux valeurs demandées (en distinguant si besoin
 Chapitre 2 - Limites et continuité pour une fonction de plusieurs
Chapitre 2 - Limites et continuité pour une fonction de plusieurs
Limites et continuité pour une fonction de plusieurs variables. Puisque la L2 Parcours Spécial - S3 - Calcul différentiel et intégral. Exemple 2.21. On ...
 Corrigé du TD no 9
Corrigé du TD no 9
petites de ε quand on manipule la définition de limite d'une fonction en un point. De plus on calcule que : f3(x) = 1. 1 − x. −. 2. 1 − x2. = 1 + x − 2.
 ficall.pdf
ficall.pdf
Fonction continue par morceaux. 362. 72 123.06 Fonctions équivalentes ... Calculer les limites des suites (u2n)n et (u2n+1)n. Indication ▽. Correction ...
 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
On dit que la fonction admet pour limite L en +? si ( ) est aussi proche de L que l' Partie 4 : Calculs de limites par composition et comparaison.
 Limites de fonctions
Limites de fonctions
Les théorèmes suivants sont très pratiques pour calculer une limite d'une fonction compliquée en la comparant à des fonctions plus simples dont on connaît la
 Les Développements Limités
Les Développements Limités
C'est clair il suffit de calculer la limite. Ce critère sert généralement à démontrer Calculons le DL de la fonction f(x) = cos x à l'ordre 3 au point ?.
 Feuille dexercices 10 Développements limités-Calculs de limites
Feuille dexercices 10 Développements limités-Calculs de limites
Etablir pour chacune des fonctions proposées ci-dessous un Calculer un développement limité de la fonction pour chacun des cas suivants :.
 LIMITES DES FONCTIONS (Chapitre 2/2)
LIMITES DES FONCTIONS (Chapitre 2/2)
Calculer la limite de la fonction f en . On a : lim. ? E. 1. . = 0 donc lim.
 Limites de fonctions
Limites de fonctions
Ce qui exprime bien que la limite de f en +? est l. Correction de l'exercice 2 ?. Généralement pour calculer des limites faisant intervenir des sommes de
 Chapitre 1 - Fonctions de plusieurs variables. Limites dans R
Chapitre 1 - Fonctions de plusieurs variables. Limites dans R
Montrer que ces fonctions sont de classe C1 sur R ou R2 et calculer leurs dérivées (partielles) en fonction des dérivées partielles de f. Exercice 17. On
 Corrigé du TD no 9
Corrigé du TD no 9
petites de ? quand on manipule la définition de limite d'une fonction en un point. Revenons à nos moutons : si l'on suppose que 1 ? ? > 0 alors.
 Fiche technique sur les limites
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +? et en 0. En + ? lim x?+? ln(x) x. =
 ficall.pdf
ficall.pdf
69 123.03 Limite de fonctions 82 125.04 Développements limités implicites ... Calculer les restes de la division euclidienne de 14
LIMITES DES FONCTIONS - Chapitre 2/2
Tout le cours en vidéo : https://youtu.be/YPwJyYDsmxMPartie 1 : Limite d'une fonction composée
Méthode : Déterminer la limite d'une fonction composéeVidéo https://youtu.be/DNU1M3Ii76k
Soit la fonction ��� définie sur !
;+∞! par : ��� 2- 1 Calculer la limite de la fonction ��� en +∞.Correction
On a : lim
1 =0, donc lim 2- 1 =2 Donc, comme limite d'une fonction composée : lim 2- 1 2 En effet, si ���→+∞, on a : ���=2- 1 →2 et donc : lim 2.Partie 2 : Limites et comparaisons
1) Théorèmes de comparaison
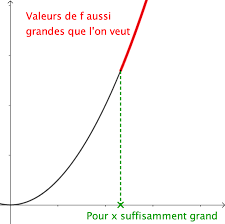
Théorèmes : Soit ��� et ��� deux fonctions définies sur un intervalle ���= - Si pour tout ��� de ���, on a : 9 lim alors lim =+∞ (Fig.1) - Si pour tout ��� de ���, on a 9 lim alors lim =-∞ (Fig.2) Remarque : On obtient des théorèmes analogues en -∞.Figure 1
Par abus de langage, on
pourrait dire que la fonction ��� pousse la fonction ��� vers +∞ pour des valeurs de ��� suffisamment grandes.Figure 2
2Démonstration dans le cas de la figure 1 :
lim =+∞ donc tout intervalle , ��� réel, contient toutes les valeurs de ���(���) dès que ��� est suffisamment grand, soit : ��� Donc dès que ��� est suffisamment grand, on a : ���Et donc lim
2) Théorème d'encadrement
Théorème des gendarmes :
Soit ���, ��� et ℎ trois fonctions définies sur un intervalle ���=Si pour tout ��� de ���, on a : >
lim lim alors lim Remarque : On obtient un théorème analogue en -∞.Par abus de langage, on pourrait dire que les fonctions ��� et ℎ (les gendarmes) se resserrent
autour de la fonction ��� pour des valeurs de ��� suffisamment grandes pour la faire tendre vers
la même limite. Ce théorème est également appelé le théorème du sandwich. Méthode : Utiliser les théorèmes de comparaison et d'encadrementVidéo https://youtu.be/OAtkpYMdu7Y
Vidéo https://youtu.be/Eo1jvPphja0
Calculer : 1) lim
���+sin��� 2) lim ���cos��� 2 +1 3Correction
1) • lim
sin��� n'existe pas. Donc sous la forme donnée, la limite cherchée est indéterminée.Levons l'indétermination :
•lim ���-1=+∞ donc d'après le théorème de comparaison : lim ���+sin���=+∞2) • lim
cos��� n'existe pas. Donc sous la forme donnée, la limite cherchée est indéterminée.Levons l'indétermination :
Et donc :
+1 ���cos(���) +1 +1 +1 F G 1 lim 1 =0 donc lim 1Et donc : lim
1 1 =0, comme limite d'un quotient.On a donc :lim
2 +1 =lim 2 +1 =0 D'après le théorème des gendarmes, on a : lim ���cos(���) 2 +1 =0.Partie 3 : Cas de la fonction exponentielle
1) Limites aux bornes
Propriétés :
lim =+∞ et lim =0Démonstration au programme :
Vidéo https://youtu.be/DDqgEz1Id2s
- La suite est une suite géométrique de raison ���>1. 4Donc, on a : lim
Si on prend un réel ��� quelconque (aussi grand que l'on veut), il existe un rang ���à partir
duquel tous les termes de la suite dépassent ���, soit : ��� La fonction exponentielle étant strictement croissante, on a également, pour toutDonc, pour tout ���>���
, on a : ���Ainsi, tout intervalle
contient toutes les valeurs de ��� , dès que ��� est suffisamment grand.Soit : lim
-lim =lim =lim , en posant ���=-���Or, lim
=+∞, donc : lim =0, comme limite d'un quotient.Soit : lim
=0. Méthode : Déterminer la limite d'une fonction contenant des exponentielsVidéo https://youtu.be/f5i_u8XVMfc
Calculer les limites suivantes :
a) lim b) lim 1Correction
a) lim -3���=-∞ • Donc, comme limite d'une fonction composée : lim =0 En effet, si ���→+∞, on a : ���=-3���→-∞ et donc : lim =0. • lim • Comme limite d'une somme : lim b) lim 1 =0, donc : lim 1- 1 =1 Donc, comme limite d'une fonction composée : lim2) Croissance comparée des fonctions exponentielles et puissances
Exemple :
Observons la fonction exponentielle et la fonction puissance ���⟼��� dans différentes fenêtres graphiques. 5 Dans cette première fenêtre, la fonction puissance semble l'emporter devant la fonction exponentielle. Mais on constate que pour ��� suffisamment grand, la fonction exponentielle dépasse la fonction puissance ���⟼��� Remarque : Dans le cas de limites infinies, la fonction exponentielle impose sa limite devant les fonctions puissances. Sa croissance est plus rapide.Propriétés (croissances comparées) :
a) lim =+∞ et pour tout entier ���, lim b) lim =0 et pour tout entier ���, lim =0Démonstration au programme du a :
Vidéo https://youtu.be/_re6fVWD4b0
- On pose ���On a : ���
6 On calcule la dérivée de la dérivée ��� -1.Et on note ���
-1Pour tout ��� strictement positif, ���
-1>0.On dresse alors le tableau de variations :
On en déduit que pour tout ��� strictement positif, ��� >0 et donc ���Soit encore :
Comme lim
2 =+∞, on en déduit par comparaison de limites que lim - Dans le cas général, on a :F���
G =N O =N 1 OOr : lim
=+∞ car on a vu que limDonc : lim
=+∞, car ��� est positif.Et donc lim
Q R =+∞, comme produit de ��� limites infinies.Soit : lim
Méthode : Calculer une limite par croissance comparéeVidéo https://youtu.be/GoLYLTZFaz0
Calculer la limite suivante : lim
2Correction
Le dénominateur comprend une forme indéterminée de type "∞-∞".Levons l'indétermination :
1+ 1- 1+ 1- 7 Par croissance comparée : lim =+∞ et de même : lim 2Donc, comme inverse de limites : lim
=lim 2 =0, donc lim 1+ =lim 1- 2 =1. Donc, lim 1+ 1- 2 1 1 =1 et donc lim 2 =1.quotesdbs_dbs47.pdfusesText_47[PDF] Limites de fonctions (Terminale)
[PDF] Limites de fonctions - Reconnaître des courbes (problème pour trouver l'extremum)
[PDF] Limites de fonctions - reconnaître des courbes - (problème pour trouver l'extremum)
[PDF] limites de fonctions cours
[PDF] limites de fonctions exercices corrigés
[PDF] limites de fonctions formes indeterminées
[PDF] limites de fonctions rationnelles exercices
[PDF] Limites de fonctions svp
[PDF] limites de fonctions terminale s
[PDF] limites de fonctions terminale s exercices
[PDF] Limites de l'organisme ? l'effort -VO2max
[PDF] limites de l'étude mémoire
[PDF] limites de l'onu
[PDF] limites de la croissance économique cours
