[PDF] Outils pour létude des fonctions

View - Download Outils pour létude des fonctions

Previous PDF

Next PDF

Outils pour l"étude des fonctions

Exercice 1Pour chacune des fonctions suivantes, préciser l"ensemble de définition et

étudier la parité.

f

1(x) = cos(x3),f2(x) = ecos(x),f3(x) = esin(x)-1,f4(x) =⎷x

4-4x2+ 3,

f

5(x) = tan?1x

,f6(x) = sin(x)ch(tanx),f7(x) =1 +x2sh(x),f8(x) =1 + ex1-ex.Exercice 2Pour chacune des fonctions suivantes, déterminer les variations sans utiliser

de dérivée, puis tracer sans calcul la courbe représentative. f

1(x) = (x-2)3,f2(x) =⎷-x,f3(x) =-1x+ 1,f4(x) = 3sin(x)sur[0,2π],

f

5(x) = sin(2x)sur[0,2π],f6(x) = 2ex-3,f7(x) = 1 + sh(-x).Exercice 3Pour chacune des fonctions suivantes, préciser l"ensemble de définition et

déterminer les variations sans calcul de dérivée : f

1(x)=ln(1+e-x),f2(x)=ch?ln(x-2)?,f3(x)=?sh(⎷x+ 3)?3,f4(x)=⎷x

2-5x+ 6.Exercice 4Soitf:R-→Rl"application définie pour toutx?Rpar

f(x) = 2|x-2| -4|x+ 1|+ 3|x|. Donner une écriture def(x)sans valeur absolue. Tracer le graphe defpuis résoudre l"équationf(x) =-3.Exercice 5 (Fonction " partie entière ») Pour tout réelx?R, il existe un unique entierntel quen6x < n+ 1. On note cet entierE(x). L"applicationE:R-→Zest appelée " fonction partie entière ».

1. CalculerE(5),E(-5),E(0,02),E(-0,02),E(3,8),E(-3,8). La fonctionEest-elle

impaire?

2. Soitx?Retn?Z. ExprimerE(x+n)en fonction deE(x)etn.

3. Tracer le graphe de l"applicationEsurR.

4. Montrer que les applicationsf:x?-→x-E(x)etg:x?-→E(4x)-4E(x)sont

périodiques et tracer leur graphe sur[-2,2].Exercice 6 (Fonctions " puissances »)

1. Simplifier les expressions suivantes :

?149 -3/2,?132 -0,8,?32243 -2/5,?272 ⎷2 2/3.

2. Donner l"allure des représentations graphiques des fonctions suivantes :

f

1:x?-→x0,25, f2:x?-→x-0,7, f3:x?-→x⎷2

, f4:x?-→πx, f5:x?-→?13? x.Exercice 7Pour chacune des applications suivantes, dire si elle est injective, surjective, bijective. f

1:?N-→N

n?-→n+ 1f2:?Z-→Z n?-→n+ 1f3:?R-→R x?-→cosx f

4:?[0,π]-→[-1,1]

x?-→cosxf5:?R-→R x?-→x4+ 3x2-5f6:?C-→R+ z?-→|z|Exercice 8Soita?R. On considère l"applicationf:R2-→R2définie, pour tout (x,y)?R2parf(x,y) = (x-y,ax+y).

1. On supposea?=-1. Montrer quefest bijective et déterminer sa réciproque.

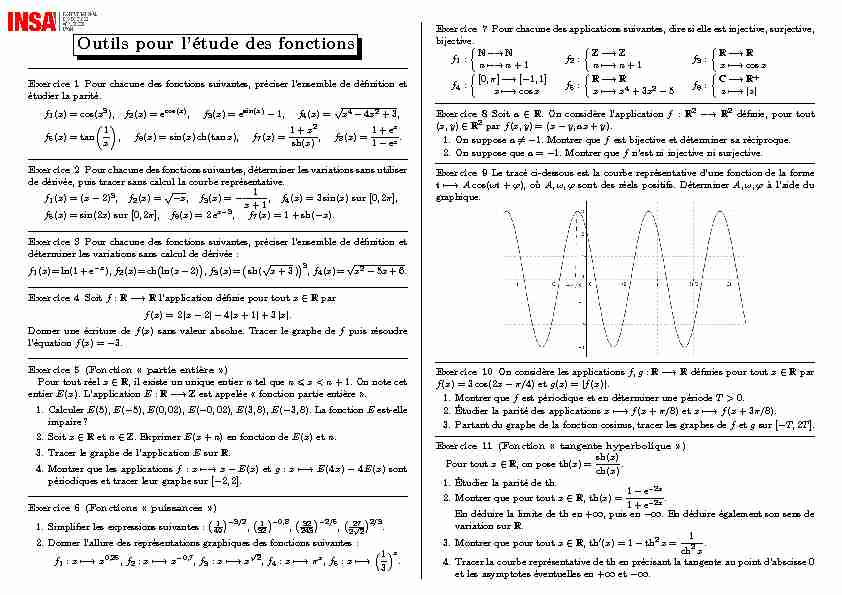
2. On suppose quea=-1. Montrer quefn"est ni injective ni surjective.Exercice 9Le tracé ci-dessous est la courbe représentative d"une fonction de la forme

t?-→Acos(ωt+?), oùA,ω,?sont des réels positifs. DéterminerA,ω,?à l"aide du graphique.Exercice 10On considère les applicationsf,g:R-→Rdéfinies pour toutx?Rpar f(x) = 3cos(2x-π/4)etg(x) =|f(x)|.

1. Montrer quefest périodique et en déterminer une périodeT >0.

2. Étudier la parité des applicationsx?-→f(x+π/8)etx?-→f(x+ 3π/8).

3. Partant du graphe de la fonction cosinus, tracer les graphes defetgsur[-T,2T].Exercice 11 (Fonction " tangente hyperbolique »)

Pour toutx?R, on poseth(x) =sh(x)ch(x).

1. Étudier la parité deth.

2. Montrer que pour toutx?R,th(x) =1-e-2x1 + e

-2x. En déduire la limite dethen+∞, puis en-∞. En déduire également son sens de variation surR.

3. Montrer que pour toutx?R,th?(x) = 1-th2x=1ch

2x.

4. Tracer la courbe représentative dethen précisant la tangente au point d"abscisse0

et les asymptotes éventuelles en+∞et-∞. Exercice 12Soitf:R-→Rl"application définie pour toutx?Rpar f(x) =1⎷x

2+x+ 1.

1. Écrire le trinômex2+x+ 1sous forme canonique.

2. Montrer que la fonctionx?-→f(x-1/2)est paire. Quelle propriété géométrique

peut-on en déduire sur le graphe def?

3. Sans utiliser la dérivée def, étudier les variations defsurRet tracer son graphe.

4. Déterminer graphiquement l"ensemblef(R).

5. Soity?R. Résoudre dansRl"équation d"inconnuexsuivante :y=f(x).

6. Déterminer alorsf(R)puis trouver les deux intervalles maximaux sur lesquels la

restriction defréalise une bijection versf(R). On écrira explicitement les bijections réciproques.Exercice 13SoitE,Fdeux ensembles etf:E-→Fune application. On suppose qu"il existe deux applicationsg:F-→Eeth:F-→Etelles queh◦f= idEet f◦g= idF. Montrer quefest bijective, queg=het quef-1=g. Application. - On noteE=R\{1,-1}. Soitf:E-→Edéfinie parf(z) =z-3z+ 1.

1. Montrer que l"on a bienf(E)?E, puis calculer(f◦f◦f)(z)pour toutz?E.

2. En déduire quefest bijective et donner l"expression de sa réciproque.Exercice 14On considère les fonctions polynômesPetQdéfinies parP(x) = 5x3-

2x+ 1etQ(x) = 2x2-1.

Calculer les fonctions polynômes suivantes et donner leurs degrés respectifs :P+Q,

P×Q,x?-→P(x2),P2,Q3,P◦Q,Q◦P,x?-→Q(x+ 1)-Q(x).Exercice 15 (Une courbe de Lissajous)

Pour chaquet?R, on définit dans un repère orthonormé le pointM(t)de coordonnées (cos(3t),sin(2t)).

1. Étudier la courbe paramétréet?[0,π/2]?-→M(t).

2. Examiner les symétries de la courbe paramétréet?[0,2π]?-→M(t); on pourra

regarder les pointsM(π-t),M(t+π).

3. Tracer alors cette courbe (courbe de Lissajousobservée par exemple sur un oscillo-

scope).

Pour les insatiables...

Exercice 16

1. Montrer que l"applicationf:N-→Zdéfinie pour toutn?Nparf(n) =n/2

sinest pair etf(n) =-(n+ 1)/2sinest impair, est bijective et déterminer sa réciproque.

2. Même question pour l"applicationg:N2-→N?définie pour tout(p,q)?N2par

g(p,q) = 2p(2q+ 1).Exercice 17Soitp,q?N?etT >0. On considère deux applicationsf,g:R-→R telles quefsoitpT-périodique etgsoitq T-périodique. Montrer que l"applicationf+g est périodique et en déterminer une période. Exemple. - Soith:R-→Rl"application définie pour toutx?Rparh(x) = 2sin( x2 )-3sin(x3 ). Déterminer une périodeTdeh. Étudier les variations dehsur[0,T] puis tracer le graphe dehsur[-T,2T].Exercice 18 (Fonctions " cosinus et sinus hyperboliques »)

1. Montrer les formules suivantes : pour tousx,y?R,

ch(x+y) = ch(x) ch(y) + sh(x) sh(y), sh(x+y) = sh(x) ch(y) + ch(x) sh(y).

2. Exprimerch(2x)en fonction dech(x), puissh(2x)en fonction dech(x)etsh(x).

3. Montrer que pour toutx?R,ch(3x) =P(ch(x))oùPest une fonction polynôme

de degré3que l"on déterminera.Exercice 19

1. Déterminer une fonction polynômePde degré3telle que l"on ait pour toutx?R,

P(x)-P(x-1) =x2. En déduire la valeur de la sommen? k=1k2pour toutn?N?.

2. Déterminer une fonction polynômePde degré4telle que l"on ait pour toutx?R,

P(x)-P(x-1) =x3. En déduire la valeur de la sommen? k=1k3pour toutn?N?.

Vérifier que

n? k=1k3=? n? k=1k? 2 .Exercice 20 (L"" astroïde ») Pour chaquet?[0,2π], on définit dans un repère orthonormé les pointsP(t),Q(t) etm(t)de coordonnées respectives(cost,0),(0,sint)et(cost,sint). On construit le pointM(t)pied de la hauteur du triangleP(t)Q(t)m(t)issue dem(t)(voir la figure ci-dessous).

1. Montrer que les coordonnées du pointM(t)sont données par(cos3t,sin3t).

2. Étudier la courbe paramétréet?[0,π/2]?-→M(t), puis examiner les symétries de

la courbe paramétréet?[0,2π]?-→M(t); on pourra regarder les pointsM(π-t), M(t+π). Tracer alors cette courbe (il s"agit d"uneastroïde, hypocycloïde à 4 points de rebroussements).-6 S SSS O xy

P(t)Q(t)m(t)

M(t)quotesdbs_dbs28.pdfusesText_34

[PDF] realiser l 'etude financiere - Formasup

[PDF] L #8482 évaluation formative

[PDF] COMMENT REALISER UNE FICHE METIER ?

[PDF] la viabilite des radios de proximite

[PDF] CONSEILS POUR REDIGER UNE FICHE DE LECTURE

[PDF] M -Guid - Méditation Chrétienne du Québec

[PDF] Construire et exporter un schéma avec X Mind - WordPresscom

[PDF] Définir une problématique de recherche - Université de Moncton

[PDF] La progression pédagogique La fiche de préparation de - Eduscol

[PDF] Pyramide des biomasses

[PDF] COMMENT FAIRE UNE RECHERCHE SUR INTERNET ?

[PDF] Comment écrire une rédaction: quelques conseils utiles

[PDF] fiche de methode : realiser une synthese ou paragraphe argumente

[PDF] LE ROUTAGE

[PDF] 7P Translations Travail avec la règle, l 'équerre et le compas Tu dois