 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
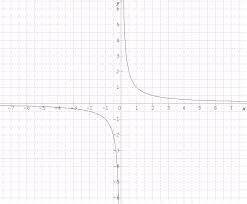
FICHE DE RÉVISION DU BAC. MATHÉMATIQUES – TOUTES SÉRIES. ÉTUDES DE FONCTIONS. LE COURS. [Série – Matière – (Option)]. 16. Limite de fonction composée : Soit f
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
Séries S – ES/L – STI2D – STL – ST2S – Mathématiques. INTÉGRATION. 1. LE COURS. [Série LE COURS. [Série – Matière – (Option)]. Dérivées de fonctions composées ...
 [PDF] Algèbre - Exo7 - Cours de mathématiques
[PDF] Algèbre - Exo7 - Cours de mathématiques
mathématiques comme les anneaux les corps
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
Plan du cours. 1. Vocabulaire. 2. Probabilités d'événements indépendants. 3 Mathématiques – Séries S – ES/L – ST2S – STMG. PROBABILITÉS DISCRETES. 6. FICHE DE ...
 Mathématiques Cours exercices et problèmes Terminale S
Mathématiques Cours exercices et problèmes Terminale S
Questions de cours. Les points suivants peuvent être abordés dans le cadre d'une restitution organisée de connais- sances (ROC) à l'épreuve écrite du bac.
 Résumé : Nombres complexes Niveau : Bac sciences
Résumé : Nombres complexes Niveau : Bac sciences
Bac Sc. expérimentales – Résumé : Nombres complexes. Définition : Remarque : Soit = + un nombre complexe donné sous forme cartésienne. - Si = 0
 fondmath1.pdf
fondmath1.pdf
La Mathématique est la reine des sciences et l'Arithmétique est la reine des Analyse
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC. Séries S – ES/L – STI2D – STL – ST2S – ST2A – hôtellerie – Mathématiques. FONCTIONS EXPONENTIELLES ET LOGARITHMES. 1. LE COURS. [Série
 Cours de probabilités et statistiques
Cours de probabilités et statistiques
IREM de Lyon - Département de mathématiques. Stage ATSM - Août 2010. Cours de bac... 65. Page 66. 66. ANNEXE C. STATISTIQUE DESCRIPTIVE UNIVARI´EE. Exemple 78 ...
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
MATHÉMATIQUES – TOUTES SÉRIES. Statistiques. LE COURS. [Série – Matière – (Option)] Plan du cours. 1. Pourcentages. 2. Moyenne et écart-type. 3. Médiane et ...
 [PDF] Études de fonction sur studyrama - FICHE DE RÉVISION DU BAC
[PDF] Études de fonction sur studyrama - FICHE DE RÉVISION DU BAC
MATHÉMATIQUES – TOUTES SÉRIES ÉTUDES DE FONCTIONS LE COURS [Série – Matière – (Option)] 1 Note liminaire Programme selon les sections :
 [PDF] TOUTES SÉRIES Statistiques - FICHE DE RÉVISION DU BAC
[PDF] TOUTES SÉRIES Statistiques - FICHE DE RÉVISION DU BAC
MATHÉMATIQUES – TOUTES SÉRIES Statistiques LE COURS [Série – Matière – (Option)] FICHE DE RÉVISION DU BAC Note liminaire
 [PDF] livre-algebre-1pdf - Exo7 - Cours de mathématiques
[PDF] livre-algebre-1pdf - Exo7 - Cours de mathématiques
proposons de partir à la découverte des maths de leur logique et de leur beauté physiques ou mécaniques des sciences du vivant de la chimie
 [PDF] fondmath1pdf
[PDF] fondmath1pdf
Licence Sciences Technologies Santé Fondamentaux des mathématiques 1 Apprendre ses cours et s'entraîner : en mathématiques le talent a ses
 [PDF] 1er BAC Sciences Mathématiques BIOF - AlloSchool
[PDF] 1er BAC Sciences Mathématiques BIOF - AlloSchool
1er BAC Sciences Mathématiques BIOF Série avec correction ensembles et application PROF : ATMANI NAJIB Application : injective et surjective et bijective
 [PDF] Cours de Mathématiques
[PDF] Cours de Mathématiques
23 mar 2011 · Cours de Mathématiques et le site http://www les-mathematiques net Dans son dictionnaire raisonné des sciences des arts et des
 [PDF] Première année du cycle du Baccalauréat international section
[PDF] Première année du cycle du Baccalauréat international section
Cours et Exercices Première année du cycle du Baccalauréat international section - sciences expérimentales Préparé par AZIZ AFAADAS Professeur
 [PDF] Cours complet de mathématiques pures T 1 / par L-B Francoeur
[PDF] Cours complet de mathématiques pures T 1 / par L-B Francoeur
Professeur de la Faculté des Sciences de Paris de l'Écolenormale et du Lycée versées dans les Mathématiques des Géographes des Marins
 [PDF] Nombres complexes Niveau : Bac sciences expérimentales Réalisé
[PDF] Nombres complexes Niveau : Bac sciences expérimentales Réalisé
Bac Sc expérimentales – Résumé : Nombres complexes Définition : Remarque : Soit = + un nombre complexe donné sous forme cartésienne
 [PDF] Cours danalyse 1 Licence 1er semestre
[PDF] Cours danalyse 1 Licence 1er semestre
Une relation porte sur des objets mathématiques comme des nombres des fonctions des figures géométriquesetc Voici quelques exemples de relations On indique
Cours et
Exercices
Première année du cycle du
Baccalauréat international
section - sciences expérimentalesPréparé par AZIZ AFAADAS Professeur
d™enseignement secondaire qualifiant au lycée OUED SAKIA EL HAMRAES - SMARA
Sommaire
Chapitre 1........................................................................ ............................................................................................... 1 La logique ........................................................................ ................. 1 Exercices ........................................................................ ............... 9 Chapitre 2........................................................................ ............................................................................................. 12Généralités sur les fonctions numériques ........................................................................
..................................................... 12 Exercices ........................................................................ ............. 24 Chapitre 3........................................................................ ............................................................................................. 25 Barycentre dans le plan ........................................................................ ...................................................................................... 25 Exercices ........................................................................ ............. 32 Chapitre 4........................................................................ ............................................................................................. 46Analytique du produit scalaire ........................................................................
........................................................................ 46 Exercices ........................................................................ ............. 57 Chapitre 5........................................................................ ............................................................................................. 49Application du produit scalaire ........................................................................
........................................................................ 49 Exercices ........................................................................ ............. 56 Chapitre 6........................................................................ ............................................................................................. 83 Les suites numériques ........................................................................ ........................................................................................ 83 Exercices ........................................................................ ............. 90 Chapitre 7........................................................................ ........................................................................................... 102 Trigonométrie ........................................................................ ...... 102 Exercices ........................................................................ ........... 109 Chapitre 8........................................................................ ........................................................................................... 112 La rotation dans le plan ........................................................................ ................................................................................... 112 Chapitre 9........................................................................ ........................................................................................... 117Limite d'une fonction numérique ........................................................................
................................................................... 117 Exercices ........................................................................ ........... 123 Chapitre 10 ........................................................................ ........................................................................................ 139La dérivabilité d'une fonction numérique ........................................................................
................................................. 139 Exercices ........................................................................ ........... 152 Chapitre 11 ........................................................................ ........................................................................................ 158Etude des fonctions numériques ........................................................................
..................................................................... 158Exercices ........................................................................................................
........................................................................... 167 Chapitre 12 ........................................................................ ........................................................................................ 191 Vecteurs de l'espace ........................................................................ ......................................................................................... 191 Chapitre 13 ........................................................................ ........................................................................................ 194Droites et plans dans l'espace ........................................................................
........................................... 194Exercice
s ........................................................................................................
........................................................................... 209 ................ 221 1. Uneassertionest une phrase soit vraie, soit fausse, pas les deux en même temps.Exemples :
-"Il pleut.» -"Je suis plus grand que toi.» -" 2Å2AE4 » -" 2£3AE7 » construites à partir dePet deQ.L"opérateur logique "et»
L'assertion "PetQ» est vraie siPest vraie etQest vraie. L'assertion "P et Q» est fausse sinon.On résume ceci en unetable de vérité:
P\QVF VVF FF FFIGURE1 - Table de vérité de "P et Q»
Par exemple siPest l'assertion "Cette carte est un as» etQl'assertion "Cette carte est cur» alors
l'assertion "P et Q» est vraie si la carte est l'as de coeur et est fausse pour toute autre carte.
L"opérateur logique "ou»
L'assertion "PouQ» est vraie si l'une des deux assertionsPouQest vraie. L'assertion "PouQ» est fausse si les deux assertionsPetQsont fausses.On reprend ceci dans la table de vérité :
P\QVF VVV FV FSiPest l"assertion "Cette carte est un as» etQl"assertion "Cette carte est coeur» alors l"assertion
"PouQ» est vraie si la carte est un as ou bien un coeur (en particulier elle est vraie pour l"as de
coeur).RemarquePour dénir les opérateurs "ou», "et» on fait appel à une phrase en français utilisant les
motsou,et! Les tables de vérités permettent d"éviter ce problème.La négation "non»
L"assertion "nonP» est vraie siPest fausse, et fausse siPest vraie.PV FnonPF VFIGURE3 - Table de vérité de "non P»
L'im?licationAE)
La dénition mathématique est la suivante :
L"assertion "(non P) ou Q» est notée "PAE)Q».Sa table de vérité est donc la suivante :
P\QVF VVF FVVFIGURE4 - Table de vérité de "PAE)Q»
L"assertion "PAE)Q» se lit en français "P implique Q». Elle se lit souvent aussi "si P est vraie alors Q est vraie» ou "si P alors Q».Par exemple :
-" 0ÉxÉ25AE)pxÉ5 » est vraie (prendre la racine carrée). -"x2]¡1,¡4[AE)x2Å3x¡4È0 » est vraie (étudier le binôme). -" sin(µ)AE0AE)µAE0 » est fausse (regarderpourµAE2¼par exemple).
-p2AE2 » est vraie! Eh oui, siPest fausse alors l"assertion "PAE)Q» est" 2Å2AE5AE)
toujours vraie.L'équivalence()
L"équivalenceest dénie par :
"P()Q» est l"assertion "(PAE)Q) et (QAE)P)».On dira "Pest équivalent àQ» ou "Péquivaut àQ» ou "Psi et seulement siQ». Cette assertion
est vraie lorsquePetQsont vraies ou lorsquePetQsont fausses. La table de vérité est :P\QV FVVF FF VExemples :
-Pourx,x??R, l"équivalence "x·x?=0??(x=0ou x?=0) » est vraie.-Voici une équivalencetoujours fausse(quelque soit l"assertionP) : "P??non(P) ».On s"intéresse davantage aux assertions vraies qu"aux fausses, aussi dans la pratique et en dehors
de ce chapitre on écrira "P??Q» ou "P=?Q» uniquement lorsque ce sont des assertions vraies. Par exemple si l"on écrit "P??Q» cela sous-entend "P??Qest vraie». Attention rien ne dit quePetQsoient vraies. Cela signie quePetQsont vraies en même temps ou fausses en même temps.Proposition 1 SoientP,Q,Rtrois assertions. Nous avons les équivalences (vraies) suivantes :1.P??non(non(P))
2. (P et Q)??(Q et P)
3. (P ou Q)??(Q ou P)
4.non(P et Q)??(non P)ou(non Q)
5.6.P et(Q ou R)non(P
ou Q)??(non P)et(non Q)¡¢??(P et Q)ou(P et R)7.
¡P ou(Q et R)¢??(P ou Q)et(P ou R)
8. "P=?Q»??"non(Q)=?non(P) »Démonstration
Voici des exemples de démonstrations :
4. Il suft de comparer les deux assertions "non(P et Q) » et " (non P)ou(non Q) » pour toutes les valeurs possibles dePetQ. Par exemple siPest vrai etQest vrai alors "PetQ» est vrai donc "non(P et Q)» est faux; d"autre part (nonP) est faux, (nonQ) est faux donc "(non P)ou(non Q)» est faux. Ainsi dans ce premier cas les assertions sont toutes les deux fausses. On dresse ainsiles deux tables de vérités et comme elles sont égales les deux assertions sont équivalentes.
P\QVF VFV FV V FIGURE6 - Tables de vérité de "non(P et Q) » et de " (non P)ou(non Q) » 6.On fait la même chose mais il y a trois variables :P,Q,R. On compare donc les tables de vérité
¢pd"abord dans le cas oùPest vrai¡(à gauche), uis dans le cas oùPest faux (à droite). Dans les
deux cas les deux assertions " P et(Q ou R) » et " (P et Q)ou(P et R) » ont la même table de vérité donc les assertions sont équivalentes.Q\RV FVVV FVF Q\RVF VFF FFF8. Par dénition, l"implication "P=?Q» est l"assertion "(non P) ou Q».
Donc l"implication "non(Q)=?non(P)» est équivalente à "non(non(Q))ou non(P)» qui équivaut
encore à "Q ou non(P) » et donc est équivalente à "P=?Q». On aurait aussi pu encore une
1.2. Quanticateurs
Le quanticateur8: "pour tout»Une assertionP?eut dé?endre d'un ?aramètrex, ?ar exem?le "x?Ê1 », l'assertionP?x? est vraie
ou fausse selon la valeur dex.L'assertion
8x2E P?x?
est une assertion vraie lorsque les assertionsP?x? sont vraies ?our tous les élémentsxde l'en- sembleE. On lit "Pour toutxappartenant àE,P?x? », sous-entendu "Pour toutxappartenant àE,P?x?est vraie».Par exem?le :
-"8x2[1,Å1[ ?x?Ê1? » est une assertion vraie. -"8x2R?x?Ê1? » est une assertion fausse. -"8n2Nn?nÅ1?est divisible par? » est vraie.Le quanticateur9: "il existe»
L'assertion
9x2E P?x?
est une assertion vraie lorsque l'on ?eut trouver au moins unxdeE?our lequelP?x? est vraie. On lit "il existe x appartenant à E tel que P?x??soit vraie)».Par exem?le :
-"9x2R?x?x¡1?Ç?? » est vraie ??ar exem?lexAE1 ?vérie bien la ?ro?riété?.- "9n2Nn?¡nÈn» est vraie ?il y a ?lein de choix, ?ar exem?lenAE3 convient, mais aussi nAE1? ou mêmenAE1??, un seul suft ?our dire que l'assertion est vraie?. -"9x2R?x?AE¡1? » est fausse ?aucun réel au carré ne donnera un nombre négatif?.La négation des quanticateurs
La négation de "8x2E P?x? » est "9x2E non P?x? » .Par exemple la négation de "8x2[1,Å1[ ?x?Ê1? » est l'assertion "9x2[1,Å1[ ?x?Ç1? ». En
effet la négation dex?Ê1 est non?x?Ê1? mais s'écrit ?lus sim?lementx?Ç1. La négation de "9x2E P?x? » est "8x2E non P?x? ».Voici des exemples : -La négation de "9z2C?z?ÅzÅ1AE?? » est "8z2C?z?ÅzÅ16AE?? ». -La négation de "8x2R?xÅ12Z? » est "9x2R?xÅ1ÝZ? ». -Ce n'est ?as ?lus difcile d'écrire la négation de ?hrases com?lexes. Pour l'assertion :8x2R9yÈ? ?xÅyÈ1??
sa négation est9x2R8yÈ?
Remarques
L'ordre des quanticateurs est très important. Par exemple les deux phrases logiques8x2R9y2R(xÅyÈ0) et9y2R8x2R(xÅyÈ0).sont différentes. La première est vraie, la seconde est fausse. En effet une phrase logique se lit de
gauche à droite, ainsi la première phrase afrme "Pour tout réelx, il existe un réely?qui ?eut donc
dé?endre dex? tel quexÅyÈ0.» (par exemple on peut prendreyAExÅ1). C'est donc une phrase
vraie. Par contre la deuxième se lit : "Il existe un réel y, tel que ?our tout réelx,xÅyÈ0.» Cette phrase est fausse, cela ne peut pas être le mêmeyqui convient pour tous lesx!On retrouve la même différence dans les phrases en français suivantes. Voici une phrase vraie
"Pour toute ?ersonne, il existe un numéro de télé?hone», bien sûr le numéro dépend de la personne.
Par contre cette phrase est fausse : "Il existe un numéro, ?our toutes les ?ersonnes». Ce serait le
même numéro pour tout le monde!Terminons avec d'autres remarques.
Quand on écrit "9x2R(f(x)AE0) » cela signie juste qu'il existe un réel pour lequelf s'annule. Rien ne dit que cexest unique. Dans un premier temps vous pouvez lire la phrase ainsi : "il existeau moinsun réelxtel quef(x)AE0 ». An de préciser quefs'annule en une unique valeur, on rajoute un point d'exclamation : 9 !x2R(f(x)AE0). Pour la négation d'une phrase logique, il n'est pas nécessaire de savoir si la phrase estfausse ou vraie. Le procédé est algorithmique : on change le "?our tout» en "il existe» et
inversement, puis on prend la négation de l'assertionP.Pour la négation d'une proposition, il faut être précis : la négation de l'inégalité stricte "Ç»
est l'inégalité large "Ê», et inversement. Les quanticateurs ne sont pas des abréviations. Soit vous écrivez une phrase en français : "Pour tout réel x, si f(x)AE1alors xÊ0.» , soit vous écrivez la phrase logique :8x2R(f(x)AE1AE)xÊ0).
Mais surtout n'écrivez pas "8xréel, sif(x)AE1AE)x?ositif ou nul». Enn, pour passer d'une ligne à l'autre d'un raisonnement, préférez plutôt "donc» à "AE)». -Il est défendu d'écrire69,6AE). Ces symboles n'existent pas!Mini-exercices 1. Écrire la table de vérité du "ou exclusif». (C'est leoudans la phrase "fromage ou dessert», l'un ou l'autre mais pas les deux.)2. Écrire la table de vérité de "non ?P et Q?». Que remarquez vous?
3. Écrire la négation de "PAE)Q».
4. Démontrer les assertions restantes de la proposition1.
5. Écrire la négation de "
¡¢P et(Q ou R) ».
6. Écrire à l'aide des quanticateurs la phrase suivante : "Pour tout nombre réel, son carré2. Raisonnements
Voici des méthodes classiques de raisonnements.2.1. Raisonnement directOn veut montrer que l'assertion "P=?Q» est vraie. On suppose quePest vraie et on montre
qu'alorsQest vraie. C'est la méthode à laquelle vous êtes le plus habitué.Exemple 1Montrer que sia,b?Qalorsa+b?Q.Démonstration
Prenonsa?Q,b?Q. Rappelons que les rationnelsQsont l'ensemble des réels s'écrivantqpavec p?Zetq?N?.? q avecp??Zetq??N?.Alorsa=qppour un certainp?Zet un certainq?N?. De mêmeb=pMaintenanta+b=pq
+p? q ?=pq?+qp?qqOr le numérateurpq?+qp?est bien un élément deZ; le dénominateurqq?est lui un élément de
N?. Donca+bs'écrit bien de la formea+b=p??q
??avecp???Z,q???N?. Ainsia+b?Q.2.2. Cas par cas
Si l'on souhaite vérier une assertionP(x) pour tous lesxdans un ensembleE, on montre l'asser- tion pour lesxdans une partieAdeE, puis pour lesxn'appartenant pas àA. C'est la méthode de disjonctionou ducas par cas.Exemple 2 Montrer que pour toutx?R,|x-1|Éx2-x+1.DémonstrationSoitx?R. Nous distinguons deux cas.
Premier cas ?xÊ1.Alors|x-1|=x-1. Calculons alorsx2-x+1-|x-1|. x2-x+1-|x-1|=x2-x+1-(x-1)
=x2-2x+2 =(x-1)2+1Ê0.Ainsix 2 -x+1-|x-1|Ê0etdoncx2-x+1Ê|x-1|.Deuxième
cas x 1 Alors x 1 x 1). Nous obtenons x 2 -x+1-|x-1|=x2-x+1+(x-1)=x2Ê0. Et donc x 2 -x+1Ê|x-1|.Conclusion.
Dans tous les cas x 1 x 2 alors non(P)DémonstrationNous supposons quenn'est pas pair. Nous voulons montrer qu'alorsn2n'est pas pair. Comme
nn'est pas pair, il est impair et donc il existek?Ntel quen=2k+1. Alorsn2=(2k+1)2=4k2+4k+1=2`+1 avec`=2k2+2k?N. Et doncn2est impair.
Conclusion : nous avons montré que sinest impair alorsn2est impair. Par contraposition ceci est équivalent à : sin2est pair alorsnest pair.2.4. Absurde
Leraisonnement par l'absurdepour montrer "P=?Q» repose sur le principe suivant : on suppose à la fois quePest vraie et queQest fausse et on cherche une contradiction. Ainsi siPest vraie alorsQdoit être vraie et donc "P=?Q» est vraie.Exemple 4 Soienta,bÊ0. Montrer que sia1+b=b1+aalorsa=b.Démonstration Nous raisonnons par l'absurde en supposant quea1+b=b1+aeta?=b. Commea1+b=b1+aalors a(1+a)=b(1+b) donca+a2=b+b2d'oùa2-b2=b-a. Cela conduit à (a-b)(a+b)=-(a-b). Commea?=balorsa-b?=0 et donc en divisant para-bon obtienta+b=-1. La somme de deux nombres positifs ne peut être négative. Nous obtenons une contradiction.Conclusion : si
a1+b=b1+aalorsa=b. Dans la pratique, on peut choisir indifféremment entre un raisonnement par contraposition ou parl'absurde. Attention cependant de bien écrire quel type de raisonnement vous choisissez et surtout
de ne pas changer en cours de rédaction!2.5. Contre-exemple
Si l'on veut montrer qu'une assertion du type "8x?E P(x) » est vraie alors pour chaquexdeE il faut montrer queP(x) est vraie. Par contre pour montrer que cette assertion est fausse alors il suft de trouver x?Etel queP(x) soit fausse. (Rappelez-vous la négation de "8x?E P(x) » est "9x?E non P(x) »). Trouver un telxc'est trouver uncontre-exempleà l'assertion "8x?
E P(x) ».Exemple 5
Montrer que l'assertion suivante est fausse "Tout entier positif est somme de trois carrés». (Les carrés sont les 02, 12, 22, 32,... Par exemple 6=22+12+12.)Démonstration
Un contre-exemple est 7 : les carrés inférieurs à 7 sont 0, 1, 4 mais avec trois de ces nombres on
ne peut faire 7.2.6. Récurrence
Leprincipe de récurrencepermet de montrer qu'une assertionP(n), dépendant den, est vraie pour tout n?N. La démonstration par récurrence se déroule en trois étapes : lors del'initialisationon prouveP(0). Pour l'étape d'hérédité, on supposenÊ0 donné avecP(n) vraie,
et on démontre alors que l'assertionP(n+1) au rang suivant est vraie. Enn dans laconclusion,Exemple 6
Montrer que pour toutn?N, 2n>n.Démonstration
PournÊ0, notonsP(n) l'assertion suivante :
2 n>n. Nous allons démontrer par récurrence queP(n) est vraie pour toutnÊ0. Initialisation.Pourn=0 nous avons 20=1>0. DoncP(0) est vraie. Hérédité.FixonsnÊ0. Supposons queP(n) soit vraie. Nous allons montrer queP(n+1) est vraie. 2 n+1=2n+2n >n+2ncar parP(n) nous savons 2n>n, >n+1 car 2nÊ1.DoncP(n+1) est vraie.
Conclusion.
Par le principe de récurrenceP(n) est vraie pour toutnÊ0, c'est-à-dire 2n>npour toutnÊ0.Remarques :
La rédaction d'une récurrence est assez rigide. Respectez scrupuleusement la rédaction proposée : donnez un nom à l'assertion que vous souhaitez montrer (iciP(n)), respectez les
trois étapes (même si souvent l'étape d'initialisation est très facile). En particulier méditez
et conservez la première ligne de l'hérédité " FixonsnÊ0. Supposons queP(n) soit vraie.
Nous allons montrer queP(n+1) est vraie. »
Si on doit démontrer qu'une propriété est vraie pour toutnÊn0, alors on commence l'initia-
lisation au rangn0. Le principe de récurrence est basé sur la construction deN. En effet un des axiomes pour dénir Nest le suivant : "SoitAune partie deNqui contient0et telle que sin?Aalors n+1?A. Alors A=N».xercice 1. (Raisonnement direct) Soienta,b?R+. Montrer que siaÉbalorsaÉa+b2ÉbetaÉ?abÉb.
2. (Cas par cas) Montrer que pour toutn?N,n(n+1) est divisible par 2 (distinguer lesn pairs desnimpairs). 3. (Contraposée ou absurde) Soienta,b?Z. Montrer que sib?=0 alorsa+b?2ÝQ. (On utilisera que?2ÝQ.)4. (Absurde) Soitn?N?. Montrer que?n
2+1 n'est pas un entier.
5. (Contre-exemple) Est-ce que pour toutx?Ron ax<2=?x2<4?
6. (Récurrence) Montrer que pour toutnÊ1, 1+2+···+n=n(n+1)2
Exercices de logique
Exercice 1Ecrire les contraposees des implications suivantes et les demontrer.nest un entier naturel,xetysont des nombres reels.1.npremier)n= 2 ounest impair ,
2.xy6= 0)x6= 0 ety6= 0 ,
3.x6=y)(x+ 1)(y1)6= (x1)(y+ 1) .
Exercice 2Ecrire les reponses aux questions suivantes, portant sur des entiers naturels, sous la forme d'assertions mathematiques (ecrites avec les symboles \?", \et", \ou", \)", \,") et les prouver.1. Le produit de deux nombres pairs est-il pair?
2. Le produit de deux nombres impairs est-il impair?
3. Le produit d'un nombre pair et d'un nombre impair est-il pair ou impair?
4. Un nombre entier est-il pair si et seulement si son carre est pair?
Exercice 3Soient les quatre assertions suivantes :1.9x2R,?y2R,x+y >0 ,
2.?x2R,9y2R,x+y >0 ,
3.9x2R,?y2R,y2> x,
4.?"2R+,92R+,jxj< ) jx2j< ".
Les assertions 1, 2, 3 et 4 sont elles vraies ou fausses? Donner leurs negations. Exercice 41. Soitn>2 un entier. Montrer par l'absurde que, sinn'est pas premier, il admet un diviseur premier?qui est inferieur ou egal apn.2. A l'aide de ce critere, determiner si les nombres 89, 167 et 191 sont premiers.
Exercice 5Montrer quep89 est irrationnel.
Exercice 6Soitn2N. Montrer que soit 4 divisen2, soit 4 divisen21.Exercice 7* Demontrer que pour toutn2N:
1.n3nest divisible par 6 ,
2.n5nest divisible par 30 ,
3.n7nest divisible par 42 .
Indication : Pour 1, on peut factorisern3npour voir que ce nombre est multiple de 2 et deExercice 8Demontrer par recurrence que :
8n2N f0;1;2;3g; n262n:
Exercice 9Pourn2N, on denit deux proprietes :
P n: 3 divise 4n1 etQn: 3 divise 4n+ 1:1. Prouver que pour toutn2N,Pn)Pn+1etQn)Qn+1.
2. Montrer quePnest vraie pour toutn2N.
3. Que penser, alors, de l'assertion :9n02N;8n2N; n>n0)Qn?
θЫЮЮСПаХЫЪCorrection 11.npair,n6= 2)nnon premier. Demo : sinpair,n6= 2 alors 2 divisen
etnn'est pas premier.2.x= 0 ouy= 0)xy= 0. D
emo triviale.3. (x+ 1)(y1) = (x1)(y+ 1))x=y. Demo : si (x+ 1)(y1) = (x1)(y+ 1) alors
en d eveloppantx+y=xy, d'ou 2y= 2x,x=y.Correction 21.
Oui.n;mpairs)nmpair. Demo :9
i;n= 2idoncnm= 2(im) est pair.2. Oui.n;mimpairs)nmimpair. Demo :9i;|,n= 2i+ 1,m= 2|+ 1 doncnm=
2(2 i|+i+|) + 1 est impair (ou par contraposee).3. Pair. (
npair,mimpair))nmpair (cf 1).4. Oui.npair,n2pair. Demo : sinpair alorsn2=nnest pair
par 1) (sens)); Sin impair alorsn2est impair par 2), ce qui donne le sens(par contraposee.1. Faux.
Negation :8x2R;9y2R;x+y60 (demo : soitx2R, on prendCorrection 3 y=x).2. Vrai (demo:y=
x+ 1). Negation :9x2R;8y2R;quotesdbs_dbs9.pdfusesText_15[PDF] cours math bac video
[PDF] cours math pdf
[PDF] cours mathematique 3eme pdf
[PDF] cours mathématique appliquée pdf
[PDF] cours mathematique bac economie pdf
[PDF] cours mathematique pdf
[PDF] cours mathematique terminale pdf
[PDF] cours maths 2 bac svt
[PDF] cours maths 6ème pdf
[PDF] cours maths bac
[PDF] cours maths bac maroc
[PDF] cours maths bts
[PDF] cours maths bts electrotechnique pdf
[PDF] cours maths bts pdf
