[PDF] 1 Lois de Kepler lois de Newton

View - Download 1 Lois de Kepler lois de Newton

Previous PDF

Next PDF

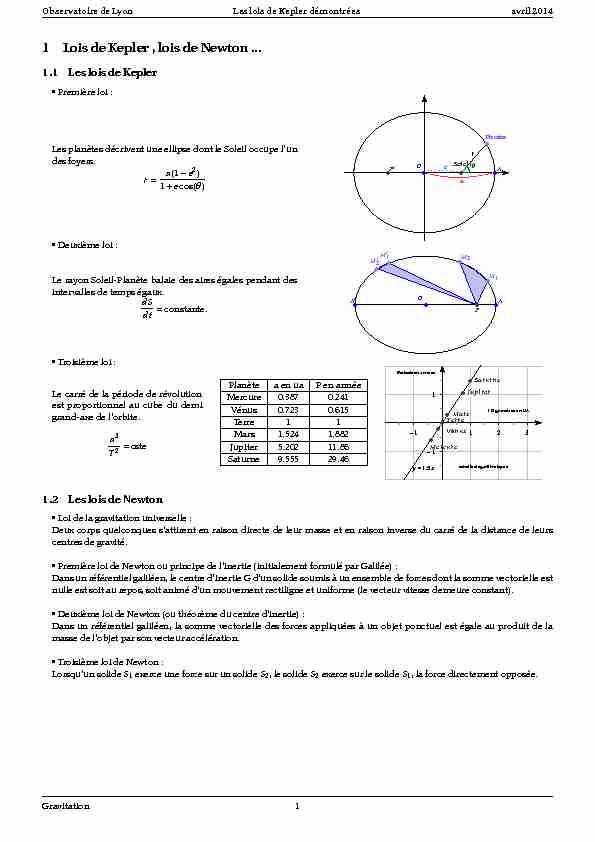
Observatoirede Lyon Leslois de Keplerdémontréesavril2014

1 Lois deKepler , lois de Newton ...

1.1 Les loisde Kepler

• Première loi : Les planètes décrivent une ellipse dont le Soleil occupe l"un des foyers. ra(1e2)

1ecos(θ)

?O ?Soleil ?F ?A ?Planète r c a • Deuxième loi : Le rayon Soleil-Planète balaie des aires égales pendant des intervalles de temps égaux. dS dtconstante. ?O F ?A ?M1 ?M2?M1 ?M2 ?A • Troisième loi :

Le carré de la période de révolution

est proportionnel au cube du demi grand-axe de l"orbite. a 3

T2cste

Planètea en uaP en année

Mercure0.3870.241

Vénus0.7230.615

Terre11

Mars1.5241.882

Jupiter5.20211.86

Saturne9.55529.46

1

11 2 311/2 grandaxe enUAPériode en années

échelleslogarithmiques

Mercure?

Vénus?

Terre?Mars?

Jupiter?

Saturne

Mercure?

Vénus?

Terre?Mars?

Jupiter?

Saturne

y1.5x

1.2 Les loisde Newton

• Loi de la gravitation universelle :

Deux corps quelconques s"attirent en raison directe de leurmasse et en raison inverse du carré de la distance de leurs

centres de gravité. • Première loi de Newton ou principe de l"inertie (initialement formulé par Galilée) :

Dansun référentiel galiléen, le centre d"inertie G d"un solide soumis à un ensemble de forcesdont la somme vectorielle est

nulle est soit au repos, soit animé d"un mouvement rectiligne et uniforme (le vecteur vitesse demeure constant).

• Deuxième loi de Newton (ou théorème du centre d"inertie) :

Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un objet ponctuel est égale au produit de la

masse de l"objet par son vecteur accélération. • Troisième loi de Newton :

Lorsqu"un solideS1exerce une force sur un solideS2, le solideS2exerce sur le solideS1, la force directement opposée.

Gravitation1

Observatoirede Lyon Leslois de Keplerdémontréesavril2014

2 Deuxième loi de Kepler: la loi des aires

On considère un corps célestePde massemsoumis à l"attraction d"un corps céleste S de masseM. Il est soumis à une force

d"attraction ?F. r rdθ (rdr)dθrdr

Sθ?

Passons en coordonnées polaires.

On arf(θ) et l"aire balayée par le rayon vecteur?rpendant l"intervalle de tempsdtest telle que : 1

2rrdθdS12(rdr)(rdr)dθ.

On en déduit :

dS1

2r2dθ.

Et : dS dt12r2dθdt.(1) ?rSP ?F S× P? S Pv v rvn D"après le principe fondamental de la dynamique, on a : Fmd?v dt(variation de la quantité de mouvement).

Le moment cinétique

?σest le moment de la quantité de mouvement, au- trement dit :

σ?rm?v.

Comme ?Fet?rsont colinéaires, on a : d dt?rmd?vdt?0.

Le moment cinétique est constant.

On a?v?vr?vn.

vret?rsont colinéaires et?σ?rm?vn..

Mais?vnrdθ

dt, alors

σmr2dθ

dtconstante.(1)

De (1) et (1"), on déduit :

dS dtσ2m12r2dθdtconstante.(2)

3 Première loi de Kepler.

3.1 Trajectoire d"un corps soumisà une accélération centrale.

ur x× S× P On considèreun corps célestePde massemsoumis àl"attrac- tion d"un corps céleste S de masseM.

On note :SPr,SP?ret?u1

r?r.

Le rayon vecteur

SP?rdu corps céleste P de massemsou-

ment mais l"énergie totale de P reste constante. On sait que l"énergie totale est :EtotECEPavec l"énergie cinétique :EC1

2mv2et l"énergie potentielle :EPGMmr.

Gravitation2

Observatoirede Lyon Leslois de Keplerdémontréesavril2014 u? v r S× P

On considère le repère mobile

P,?u,?u

. DeSPr?u, on déduit par dérivation : vdr dt?urdθdt?u.

On a donc :?v2dr

dt 2 r2dθdt 2

Et par conséquent :

E tot1

2mv2GMmr12mdrdt

2 r2dθdt 2 GMmr.

D"après la loi des aires :

dS dtest une constante, on en déduit donc que :r2dθdtconstanteK.

Et finalement :dθ

dtKr2. En remplaçant dans l"expression de l"énergie totale, on obtient : E tot1

2mdrdt

2 r2Kr2 2 GMmr.

Ou encore :

E tot1

2mdrdt

2 K2r2 GMmr.

Effectuons un changement de variable...On a :

dr dtdrdθdθdtKr2drdθ. On en déduit une autre expression de l"énergie totale : E tot1

2mKr2drdθ

2 K2r2 GMmr 1

2mK2r2

1r2drdθ

2 1 GMmr Effectuons un autre changement de variable en posant : 1 ru. On a alors en différenciant par rapport àθ:1 r2drdθdudθdont on déduit :drdθr2dudθ. On en tire une autre expression de l"énergie totale en fonction deu: E tot1

2mK2u2

r

2dudθ

2 1 GMmu 1

2mK2dudθ

2 u2 GMmu

L"énergie totale est constante, alors si on dérive l"expression précédente par rapport àθ, on obtient :

01 2mK2

2dudθd

2udθ22ududθ

GMmdudθ

0mK2du

dθd

2udθ2ududθ

GMmdudθ

0mdu dθ K

2d2udθ2u

GM

0K2d2u

dθ2u GM K2d2u dθ2u GM d2u dθ2uGMK2

Gravitation3

Observatoirede Lyon Leslois de Keplerdémontréesavril2014 Cette équation différentielle admet comme solution :u1rAcos(θθ0)GMK2.

On en déduit :r1

Acos(θθ0)GMK2.

On pose :(3)

1 pGMK2,(4)eAp; ce qui donne : rp ecos(θθ0)1.

On reconnait l"équation polaire d"une conique d"excentricitée, de paramètrep, oùθ0est l"angle que fait le grand axe de la

conique avec l"axe polaire à l"origine des temps. • Sie0, la conique est un cercle. • Si 0e1, la conique est une ellipse. • Sie1, la conique est une parabole. • Sie1, la conique est une hyperbole.

3.2 Cas de l"ellipse

p OFc OAa? F? F A? P O

Prenons :θ00 etrpecosθ1.

Avecθπ

2,rpPF.

Par définition de l"ellipse on a :PFp,PFPF2aet

comme

PFF90o:FF2PF2PF2.

On en déduit :

pPF2a p

2(2c)2PF2PF2ap

p

2(2c)2(2ap)2

PF2ap p

24c24a24app2PF2ap

c 2a2ap

Maisec

aetc2e2a2, alorspaae2a(1e2) et finalement : ra(1e2) ecosθ1. • Périhélie pourθ0, cosθ1 etra(1e) • Aphélie pourθ180o, cosθ1 etra(1e)

4 Troisième loi deKepler

On a vu que :

rp ecos(θθ0)1,oùpa(1e2).

D"après (2)

dS dtK2et en intégrant :S(t)σ2mtK2t. Sur une périodePpour une ellipse de grand axeaet de petit axeb, on a :S(P)πabK

2Pet (6) :(πab)2K2P

2

On a vu au 3.2 que :pa(1e2).

De (3), on déduit :K2GMpetK2GMa(1e2).

D"autre part :b2a2(1e2), alors (6) donne :

πa2a2(1e2)K2

4P2π2a2a2(1e2)K2P24

π2a2a2(1e2)GMa(1e2)P2

4

GMa(1e2)P2

4π2a3GMP24

a3

P2GM4π2.

Gravitation4

Observatoirede Lyon Leslois de Keplerdémontréesavril2014

5 Orbite des planèteset équation deKepler.

E est une ellipse d"excentricitée, de centre O de grand axea, de petit axeba

1e2et de foyersFetF.

On considère C le cercle de centre O et de rayona. M" est le point de C qui a même abscisse que le point M de l"ellipse. On va remplacerretθpar une variable unique : l"anomalie excentriqueu, oùuest l"angle que forme le rayonOMavec avec l"axe des abscisses.

On va exprimerren fonction deuetdθ

dten fonction deu. ×O C

×M?

M

A×P×F×F

×H r uθ

5.1 Expression deren fonction deu.

Soityl"ordonnée de M etycelle de M".

Pour M, on a :

x2 a2y2b21.

Pour M" on a :

x2 a2y2a21. En soustrayant terme à terme ces deux relations, on obtient : y2 b2y2a2yyba. Orba

1e2, alorsyy1e2.

De OMOFFM, on déduit :xacosucrcosθrcosθacosuca(cosue).

DeOMOFFM, on déduit :yasinuy

On a les deux relations :

rcosθa(cosue) rsinθasinu 1e2
On élève au carré et on ajoute terme à terme; on obtient : r

On a finalement :

(I):ra(1ecosu).

5.2 Expression de

dθ dten fonction deu. rcosθa(cosue) ra(1ecosu)r cos 2θ 2 sin2θ2 a(cosue) r cos 2θ 2 sin2θ2 a(1ecosu) Par addition et par soustraction des égalités précédentes,on obtient :quotesdbs_dbs28.pdfusesText_34

[PDF] Chimie : 2nde Contrôle : Classification périodique des éléments

[PDF] EAJE - JIRP

[PDF] Evaluation Français : La poésie engagée - Eklablog

[PDF] Corrigé - Académie en ligne

[PDF] Classe 3ème MATHEMATIQUES NOM : 22/04/10 CONTROLE n° 13

[PDF] CLASSE : 3ème CONTROLE sur le chapitre : PUISSANCES ET

[PDF] PYRAMIDES ET CONES La calculatrice est autorisée EXERCICE 1

[PDF] Université Hassan II - Casablanca Présentation - FSTM

[PDF] Les 7 outils du Contrôle de la Qualité - UTC

[PDF] LA REGLEMENTATION DES CHAUDIÈRES

[PDF] Evaluation3 : Solutions et concentrations massiques CORRECTION

[PDF] ENTRETIENS, CONTROLES ET VERIFICATIONS TECHNIQUES

[PDF] Principales vérifications périodiques - INRS

[PDF] Corrigé Fiches d 'activités Sciences et techniques - EM consulte

[PDF] CLASSE : 3ème CONTROLE sur le chapitre : STATISTIQUES ET