 de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n˚1
de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n˚1
Calculer la fonction dérivée de f et étudier son signe. 4. Dresser le tableau de variations de f. 5. Tracer la courbe représentative de f. Corrigé. Exercice n˚2
 TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
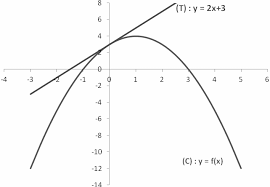
Tracer sommairement la courbe (C) et la tangente (T). Exercice 2. Etude d'une fonction polynôme du 3ème degré. Soit la fonction de la variable réelle définie
 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
2001 . 4. Soit f la fonction trinôme telle que ( ). 2. f x ax bx c.
 TD-ETUDE DES FONCTIONS
TD-ETUDE DES FONCTIONS
TD- ETUDE DES FONCTIONS avec exercices d'applications et réflexions avec solutions. PROF: ATMANI NAJIB. 1BAC SM BIOF. Exercice1 : Soit la fonction f définie
 exercices-avec-solutions-sur-l-etude-des-fonctions.pdf
exercices-avec-solutions-sur-l-etude-des-fonctions.pdf
Exercices corrigés. 1. PROF : ATMANI NAJIB. 1er BAC Sciences Expérimentales BIOF http://xriadiat.e-monsite.com etude de fonctions. Page 2. Correction de l'
 ficall.pdf
ficall.pdf
Fonction continue par morceaux. 362. 72 123.06 Fonctions équivalentes ... Exercice 868. Trouver un polynôme P de degré ⩽ 2 tel que. P(1) = −2 et P(−2) ...
 FONCTION LOGARITHME NEPERIEN EXERCICES CORRIGES
FONCTION LOGARITHME NEPERIEN EXERCICES CORRIGES
L'étude du signe de. ( ) 2. 2 1. g x x x. = −. + est plus simple puisque pour tout réel x . ( ) ( )2. 1. g x x. = −.
 Corrigé des exercices sur létude de fonctions h h h h h
Corrigé des exercices sur létude de fonctions h h h h h
Corrigé des exercices sur l'étude de fonctions. TS. Corrigé des exercices sur l'étude de fonctions. Dérivabilité. La fonction f définie par f x =x x est
 Etude de fonctions
Etude de fonctions
Etude de fonctions. Exercices de Jean-Louis Rouget. Retrouver aussi cette fiche Correction de l'exercice 1 Α. 1. f1 est définie et de classe C∞ sur R∗ en ...
 Corrigé du TD no 9
Corrigé du TD no 9
Par un raisonnement semblable à celui de l'exercice précédent on en déduit que la fonction x ↦→ cos. (1 x. ) n'admet pas de limite en 0. Exercice 8 a) D
 de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n?1
de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n?1
Calculer la fonction dérivée de f et étudier son signe. 4. Dresser le tableau de variations de f. 5. Tracer la courbe représentative de f. Corrigé. Exercice
 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
Exercices corrigés Fonctions. Exercices corrigés. Fonctions. 1. Généralités + sur (calcul de la dérivée étude de son signe
 TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
Etude de fonctions polynômes. ? Etude de fonctions rationnelles. Exercice 1. Etude d'une fonction polynôme du 2nd degré. Soit la fonction de la variable
 EXERCICES ÉTUDES DE FONCTIONS
EXERCICES ÉTUDES DE FONCTIONS
4°) Tracer la courbe (Cf) de f. EXERCICE 02. Soit f une fonction dont le tableau de variation est le suivant : La fonction f est de la forme :.
 Fascicule dexercices
Fascicule dexercices
Sommaire des exercices. 1. Logarithmes et exponentielles. 2. Dérivées et différentielles - Fonction d'une variable. 3. Etude de fonctions.
 ficall.pdf
ficall.pdf
Tous les exercices. Table des matières. 1 100.01 Logique 70 123.04 Etude de fonctions ... 91 127.04 Intégration à l'aide d'une fonction auxiliaire.
 exercices-avec-solutions-sur-l-etude-des-fonctions.pdf
exercices-avec-solutions-sur-l-etude-des-fonctions.pdf
Exercice 1. Exercices corrigés. 1. PROF : ATMANI NAJIB. 1er BAC Sciences Expérimentales BIOF http://xriadiat.e-monsite.com etude de fonctions
 MATH Tle D OK 2
MATH Tle D OK 2
Les corrigés sont pour confirmer leurs justes réponses ou donner d'autres pistes de résolution qui ne sont peut-être pas les leurs. Le succès résulte de
 livre-analyse-1.pdf - Exo7 - Cours de mathématiques
livre-analyse-1.pdf - Exo7 - Cours de mathématiques
études de fonctions au tracé de courbes paramétrées et à la résolution toutes les vidéos correspondant à ce cours ainsi que des exercices corrigés.
 Limite continuité
Limite continuité
dérivabilité
Le plan est rapporté à un repère orthogonal(O;-→ı;-→?)d"unité1cm surOxet0,5cm surOy.
Partie A : Étude d"une fonction polynôme de degré2 On noteCfla courbe représentative de la fonctionfdéfinie sur[-3,4]par f(x) =3 2x2-11. (a) Déterminerf?, la fonction dérivée def.
(b) Établir le tableau devariation defsur[-3;4].2. Déterminer une équation deT, la tangente à la courbeCfau point d"abscisse-1.
3. Tracer la tangenteTpuisla courbeCfdans le repère(O;-→ı;-→?)
Partie B : Étude d"une fonction polynôme de degré3 On considèreCg, la courbe représentative de la fonctiongdéfinie sur[-3,4]par g(x) =-x3+32x2+ 6x-1
1. (a) Déterminer la fonction dérivéeg?.
(b) Étudier le signe deg?(x). En déduire le tableau de variation degsur[-3,4]. (c) Combien l"équationg(x) = 0admet-elle de solution(s) sur[-3,4](Justifier).On noteαla plus grande de ces solutions.
(d) Déterminer un encadrement deαd"amplitude10-2.2. Déterminer, par le calcul, les coordonnées des points d"intersection des courbesCfetCg.
3. Tracer la courbeCgdans lerepère orthogonal(O;-→ı;-→?).
Partie A
1. (a) On trouvef?(x) = 3x
(b) d"où le tableau de variations : x-3 0 4Signe def?(x)-0 +
25223
Variations def? ?
-12. On af(-1) =1
2etf?(-1) =-3d"où l"équation de latangente cherchée est :
y=f?(-1)(x+ 1) +f(-1) =-3(x+ 1) +12=-3x-5
23. Voir graphe
Partie B
1. (a) Le calcul de la fonction dérivée donneg?(x) =-3x2+ 3x+ 6
(b) Pour déterminer le signe deg?(x), on calcule le discriminantΔ, ici égal à81, ce qui nous donne
les deux racinesx1= 2etx2=-1.Or, un polynôme du second degré est du signe dea(ici négatif) sauf entre les racines d"où le
tableau de variations deg: x-3-1 2 4Signe deg?(x)-0 + 0-
4329
Variations deg? ? ?
-9 2-17 (c)gest strictement décroissante sur l"intervalle[-3;-1]avecg(-3)>0etg(-1)<0. L"équationg(x)=0admet donc une unique solution sur l"intervalle[-3;-1]. gest strictement croissante sur l"intervalle[-1;2]avecg(-1)<0etg(2)>0. L"équationg(x) = 0admet donc une unique solution sur l"intervalle[-1;2]. gest strictement décroissante sur l"intervalle[2;4]avecg(2)>0etg(4)<0. L"équationg(x) = 0admet donc une unique solutionαsur l"intervalle[2;4]. Conclusion : L"équationg(x) = 0admet donc trois solutions sur l"intervalle[-3;4].(d)αappartient à l"intervalle[2;4], de plus,g(3) = 3,5qui est positif. On fait donc une table de
valeurs avec la calculatrice avec des valeurs allant de3à4par pas de0,1. On trouveg(3,2) = 0,79>0etg(3,3) =-0,80<0donc :3,2< α <3,3. On réitère le même procédé cette fois-ci sur l"intervalle[3,2;3,3]par pas de0,01. On obtientg(3,25) = 0,02>0etg(3,26) =-0,14<0donc :3,25< α <3,26.2. Pour déterminer l"intersection des deux courbes, il faut résoudre le système
y=f(x) y=g(x)On obtient alorspourx:3
2x2-1 =-x3+3
2x2+ 6x-1?? -x3+ 6x= 0??x(-x2+ 6) = 0
d"où les solutions :x= 0,x=⎷6etx=-⎷6 Les points d"intersection sont donc les points : A (-⎷6 8 ), B (0 -1 )et C ⎷6 8 3.1 2 3-1-2-3
2 4 6 8 10 12 14 16 18 20 22-2 -4 -6 -8 -10 -12 -14 -16 -18 Cg Cf T ?A B ?C -f(x)=x2-x+1
2-xpourx?=2.-g(x)=sinx
xpourx?=0.1. (a) Déterminer la limite defen+∞et en-∞.
(b) Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCfen±∞?
2. Montrer que pour toutx>0 on a :
-1 xEn déduire la limite degen+∞.
Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCgen+∞?3. Déterminer,envousinspirantdelaquestionprécédente,lalimitedegen-∞etendéduirel"existenced"uneasymp-
tote àCgen-∞que l"on précisera.4. (a) Etablir le tableau de signe de 2-x.
(b) En déduire les limites defen 2+puis en 2-; en déduire l"existence d"asymptote àCfque l"on précisera.
5. (a) Pour toutx?=2 calculerf?(x).
(b) Etudier le signe def?(x) en fonction dex. (c) Dresser le tableau de variation complet defsur ]-∞;2[?]2;+∞[.Exercice -f(x)=-x2+x+1 x-1pourx?=1.-g(x)=cosx+1 xpourx?=0.1. (a) Déterminer la limite defen+∞et en-∞.
(b) Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCfen±∞?
2. Montrer que pour toutx>0 on a :
xEn déduire la limite degen+∞.
Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCgen+∞?3. Déterminer,envousinspirantdelaquestionprécédente,lalimitedegen-∞etendéduirel"existenced"uneasymp-
tote àCgen-∞que l"on précisera.4. (a) Etablir le tableau de signe dex-1.
(b) En déduire les limites defen 1+puis en 1-; en déduire l"existence d"asymptote àCfque l"on précisera.
5. (a) Pour toutx?=1 calculerf?(x).
(b) Etudier le signe def?(x) en fonction dex. (c) Dresser le tableau de variation complet defsur ]-∞;1[?]1;+∞[. On considère les fonctionsfetgdéfinies par : -f(x)=x2-x+12-xpourx?=2.-g(x)=sinx
xpourx?=0.1. (a)Déterminer la limite defen+∞et en-∞.
On transforme l"expressionf(x) (because FI) :
Pour toutx?=0 :
f(x)= x2 1-1 x+1 x2 x ?2 x-1 ?=x 1-1 x+1 x2 2 x-1On a :
limx→±∞ 1-1 x+1 x2 2 x-1 =1 -1=-1 Et limx→+∞x=+∞donc par produit on obtient : limx→+∞f(x)=-∞ De même comme limx→-∞x=-∞on a par produit : limx→-∞f(x)=+∞(b)Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCfen±∞?
Les limites en±∞defvalent±∞on ne peut donc pas en déduire l"existence d"asymptote horizontale.
2.Montrer que pour toutx>0 on a :
-1 x xEn déduire la limite degen+∞.
On alimx→+∞-1
x=0=limx→+∞ 1 xdonc d"après le théorème des gendarmes on a : limx→+∞g(x)=0 Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCgen+∞?Du résultat précédent on déduit queCgadmet une asymptote horizontale d"équationy=0 en+∞.
3.Déterminer, en vous inspirant de la question précédente, la limite degen-∞et en déduire l"existence d"une asymptote àCgen-∞que l"on
précisera. On refait la même chose mais pourx<0, ce qui donne : x≥sinx x≥1 xOn a limx→-∞-1
x=0=limx→-∞ 1 xdonc d"après le théorème des gendarmes on a : limx→-∞g(x)=0 On en déduit queCgadmet une asymptote horizontale d"équationy=0 en-∞.4. (a)Etablir le tableau de signe de 2-x.
(b)En déduire les limites defen 2+puis en 2-; en déduire l"existence d"asymptote àCfque l"on précisera.
D"après le tableau de signe précédent lorsquex>2 on a 2-x<0 par conséquent : limx→2+2-x=0- De plus limx→2+x2-x+1=4-2+1=3, par quotient on obtient alors : limx→2+f(x)=-∞De même, lorsquex<2 on a 2-x>0 donc :
limx→2-2-x=0+ De plus limx→2-x2-x+1=4-2+1=3, par quotient on obtient alors : limx→2-f(x)=+∞ On en déduit l"existence d"une asymptote verticale d"équationx=2.5. (a)Pour toutx?=2 calculerf?(x).
Pour toutx?=2fest dérivable et on a :
f?(x)=(2x-1)(2-x)-(-1)×(x2-x+1) (2-x)2=4x-2x2-2+x+x2-x+1 (2-x)2=-x2+4x-1 (2-x)2 (b)Etudier le signe def?(x) en fonction dex. Pourtoutx?=2,(2-x)2>0doncf?(x)estdusignede-x2+4x-1,polynôme dontnousallonsdresserletableau de signe.Δ=16-4=12, ce polynôme admet deux racines :
x1=-4+?12 -2=2-?3 etx2=2+?3On obtient alors le tableau de signe def?:
x-∞2-?322+?3+∞ f?(x)-0++0- (c)Dresser le tableau de variation complet defsur ]-∞;2[?]2;+∞[. On déduit du tableau de signe de la dérivée : x-∞2-?322+?3+∞ f?(x)-0++0- f(x) f(2-?3) f(2+?3) x-∞2+∞2-x+0-
On considère les fonctionsfetgdéfinies par : -f(x)=-x2+x+1 x-1pourx?=1.-g(x)=cosx+1 xpourx?=0.1. (a)Déterminer la limite defen+∞et en-∞.
On transforme l"expressionf(x) (because FI) :
Pour toutx?=0 :
f(x)= x2 -1+1 x+1 x2 x 1-1 x ?=x -1+1 x+1 x2 1-1 xOn a :
limx→±∞ -1+1 x+1 x2 1-1 x =-1 1=-1 Et limx→+∞x=+∞donc par produit on obtient : limx→+∞f(x)=-∞ De même comme limx→-∞x=-∞on a par produit : limx→-∞f(x)=+∞(b)Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCfen±∞?
Les limites en±∞defvalent±∞on ne peut donc pas en déduire l"existence d"asymptote horizontale.
2.Montrer que pour toutx>0 on a :
x xEn déduire la limite degen+∞.
On alimx→+∞0=0=limx→+∞
2 xdonc d"après le théorème des gendarmes on a : limx→+∞g(x)=0 Peut-on en déduire l"existence d"une asymptote pour la représentation graphiqueCgen+∞?Du résultat précédent on déduit queCgadmet une asymptote horizontale d"équationy=0 en+∞.
3.Déterminer, en vous inspirant de la question précédente, la limite degen-∞et en déduire l"existence d"une asymptote àCgen-∞que l"on
précisera. On refait la même chose mais pourx<0, ce qui donne : x≥2 xOn a limx→-∞0=0=limx→-∞
2 xdonc d"après le théorème des gendarmes on a : limx→-∞g(x)=0 On en déduit queCgadmet une asymptote horizontale d"équationy=0 en-∞.4. (a)Etablir le tableau de signe dex-1.
x-∞1+∞ x-1-0+(b)En déduire les limites defen 1+puis en 1-; en déduire l"existence d"asymptote àCfque l"on précisera.
D"après le tableau de signe précédent lorsquex>1 on ax-1>0 par conséquent : limx→1+x-1=0+ De plus limx→1+-x2+x+1=-1+1+1=1, par quotient on obtient alors : limx→1+f(x)=+∞De même, lorsquex<1 on ax-1<0 donc :
limx→1-x-1=0- De plus limx→1--x2+x+1=-1+1+1=1, par quotient on obtient alors : limx→1-f(x)=-∞ On en déduit l"existence d"une asymptote verticale d"équationx=1.5. (a)Pour toutx?=1 calculerf?(x).
Pour toutx?=1fest dérivable et on a :
f?(x)=(-2x+1)(x-1)-1×(-x2+x+1) (x-1)2=-2x2+2x+x-1+x2-x-1 (x-1)2=-x2+2x-2 (x-1)2 (b)Etudier le signe def?(x) en fonction dex. Pourtoutx?=1,(x-1)2>0doncf?(x)estdusignede-x2+2x-2,polynôme dontnousallonsdresserletableau de signe.Δ=4-8= -4<0, ce polynôme n"admet pas de racine donc il est de signe constant. Ici on a pour toutx?=1,
-x2+x+1<0. On obtient alors le tableau de signe def?: x-∞1+∞ f?(x)-- (c)Dresser le tableau de variation complet defsur ]-∞;1[?]1;+∞[. On déduit du tableau de signe de la dérivée : x-∞1+∞ f?(x)-- f(x)1. On considère la fonction g définie sur l"intervalle I = [ 0 ;4p] par g(x) = tan(x) - x .
a) Etudier les variations de la fonction g et en déduire son signe. b) Montrer que, pour tout x de I, on a 0£tan( x)£1.c)On considère la fonction h définie sur I par h(x) = tan(x) - 2x . Montrer que la dérivée de h peut s"écrire
h"( x)=tan2( x)-1. Etudier les variations de h et en déduire son signe .2. On considère la fonction f définie sur I par f(x) =
343 x tan( x)-x- .
a) Montrer que la dérivée de f peut s"écrire f "( x)=(tan( x)+2x)(tan( x)-2x). En déduire le signe de f " .
b) Dresser le tableau de variations de la fonction f et en déduire son signe. c) Montrer que, pour tout x de I, on a 343 xx£tan( x)£x+.
3. Calculer les deux limites suivantes :20
0 x x tanx-x limx® et 4 1 4 x tanxlim1. a) La fonction g est dérivable comme somme de fonctions dérivables ; g"(x)=tan2(x)+1-1=tan2(x)est positif ;
donc la fonction g est croissante sur I et comme g(0) = 0, la fonction g est positive sur I. b) Pour tout x de I, on a22£cos( x)£1 donc 11cos( x)£ £2et 202£sin( x)£, donc 0£tan( x)£1.
c) La fonction h est dérivable comme somme de fonctions dérivables ; h"( x)=tan2(x)+1-2=tan2( x)-1 ; d"après la
question précédente, h"(x) est négative et donc h est décroissante sur I ; de plus, h(0) = 0, donc h est négative sur I.
2. a) La fonction f est dérivable comme somme de fonctions dérivables ; f "( x)=tan2( x)+1-1-4x2=tan2( x)-4x2 ;
donc f "( x)=(tan( x)+2x)(tan( x)-2x) ; d"après les questions précédentes, tan( x)-2x£0 et tan( x)+2x³0 donc
f"(x) est négative et donc f est décroissante sur I ; de plus, f(0) = 0, donc f est négative sur I.
b) Le tableau de variations de f :( Le signe de f sur I : f(x) £ 0 ) c) Pour tout x de I, on a g( x)³0et f(x) £ 0, donc 343 xx£tan( x)£x+.
3. Pour tout x de I, on a
34 03x£tan( x)-x£ et si x ¹ 0, 2403 tan( x)-x£x x£. Comme 00 4 3xx x lim=0alors 200 0 xx tanx-xlimx® = . La fonction tangente est dérivable sur I, donc 4 1 4 x tanxlim est le nombre dérivé de tan(x) en 4p, car 14tan( )p=; donc2quotesdbs_dbs13.pdfusesText_19
[PDF] etude de fonction exercice terminale s
[PDF] etude de fonction ln exercice corrigé
[PDF] etude de fonction logarithme exercice corrigé
[PDF] étude de fonction terminale s exercice corrigé pdf
[PDF] etude de gestion stmg carrefour
[PDF] etude de gestion stmg exemple de sujet
[PDF] etude de gestion stmg problematique
[PDF] etude de l acide ascorbique
[PDF] etude de l'acide ascorbique
[PDF] étude de l'ocde sur la gestion des risques au maroc
[PDF] etude de marché d'un projet
[PDF] etude de marché fromage
[PDF] etude de marché huile d'olive
[PDF] etude de marché lait
