Limites et asymptotes
Remarque : Une fonction n'a pas nécessairement de limite (finie ou infinie) Remarque : Avec ces régles de calcul et quelques transformations on peut trouver n' ...
Chapitre 9: Identifier la position des asymptotes dune fonction grâce
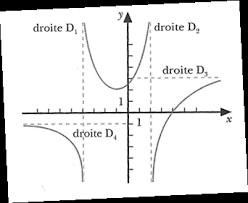
Asymptote verticale : La fonction f est discontinue en x = -4 et x = 2 car il y a présence d'asymptotes verticales à ces endroits
5. Études de fonctions
Chercher les zéros puis faire un tableau pour voir où la fonction est négative
Comment trouver les asymptotes dans un tableau de variations
Et il ne pourra donc y avoir que des asymptotes horizontales (ou éventuellement obliques ). X. 2. +00. Variations de la fonction. 3. On a. On a lim. : 26 f(x) =
La fonction rationnelle
D Comment identifier des asymptotes verticales d'une fonction rationelle ? D On a déjà l'ordonnée il reste à trouver les abscisses. Pour cela
Chapitre 4 - Limites et Asymptotes
Remarque 1.1 A l'infini une fonction polynomiale se comporte comme son terme de plus haut degré. Exercice 2.1 Calculer les limites suivantes. 1. lim x→∞. 2x3
6. Études de courbes paramétrées
Les flèches indiquent comment évolue la courbe en fonction de t. 1. Commencez par Trouver les asymptotes d'une courbe paramétrée. ok. Trouver les points ...
Fiche methodes :Etude de fonctions - AlloSchool
Calculer la ou les asymptotes affines et si demandé
Etude de branches infinies. 1 Démarche
f(x)=+∞. La fonction f n'admet alors pas d'asymptote horizontale en +∞ et l'on doit poursuivre l'étude pour étudier de plus pr`es le comportement de f(x)
LIMITES DES FONCTIONS
Démontrer que la courbe représentative de la fonction admet des asymptotes dont on précisera la nature et les équations. Calculer la limite de la fonction ...
Chapitre 9: Identifier la position des asymptotes dune fonction grâce
Asymptote verticale : La fonction f est discontinue en x = -4 et x = 2 car il y a présence d'asymptotes verticales à ces endroits
Limites et asymptotes
Définition 1 : Soit f une fonction définie au moins sur un intervalle du type [a de calcul et quelques transformations on peut trouver n'importe quelle.
La fonction rationnelle
D Comment identifier des asymptotes verticales d'une fonction rationelle ? On a déjà l'ordonnée il reste à trouver les abscisses.
Limites de fonctions
Technique : pour trouver les asymptotes verticales éventuelles au graphique d'une fonction f il faut déterminer les réels qui n'appartiennent pas à dom f
6. Études de courbes paramétrées
coordonnées des points de la courbe sont exprimées en fonction d'un paramètre. (souvent noté t k
Objectif du cours: Fonction tangente
Pour tracer la fonction tangente. 1- (h k). 2- La moitié de la période à l'aide du paramètre b (P/2) (ou trouver l'asymptote). 3- Asymptotes: à partir de
Limites asymptotes EXOS CORRIGES
Trouver deux fonctions f et g telles que lim ( ) 2) Etudier le comportement de f en + ? (limite asymptote sur la courbe). Exercice n°24.
LIMITES DES FONCTIONS
Remarque : Lorsque tend vers +? la courbe de la fonction "se rapproche" de son asymptote. 2) Limite infinie à l'infini. Intuitivement : On dit que la
Fonction exponentielle et asymptotes
Démontrer que f est une fonction impaire c'est à dire que pour tout réel x
TRACE DE DIAGRAMME DE BODE
Pour tracer le diagramme de 20 log en fonction de log w on peut commencer par étudier le Ces deux asymptotes se rejoignent lorsque : . ... on trouve :.
Année 2005-20061èreS
Chap V :Limites et asymptotes
I. Limites en l"infini
1) Limite infinie à l"infini
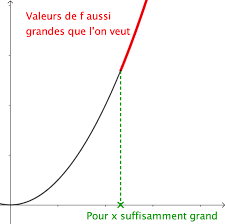
Définition 1 :Soitfune fonction définieau moinssur un intervalle du type[a;+∞[: On dit quefa pour limite+∞en+∞et on notelimx→+∞f(x) = +∞sif(x)est aussi grand que l"on veut dès quexest assez grand ( Lorsqu"on dit grand, on sous-entend positif ). faire le lien avec tableau de variationsExemple :limx→+∞x= +∞;limx→+∞x2= +∞;limx→+∞x3= +∞;limx→+∞⎷x= +∞
On définit de mêmelimx→+∞f(x) =-∞parf(x)est aussi grand dans les négatifs que l"on veut dès
quexest assez grand.On définit encore de manière analoguelimx→-∞f(x) = +∞,limx→-∞f(x) =-∞
(attention toutefois à l"ensemble de définition). Exemple :limx→-∞x=-∞;limx→-∞x2= +∞;limx→-∞x3=-∞2) Limite finie à l"infini
Définition 2 :Soitfune fonction définieau moinssur un intervalle du type[a;+∞[: On dit quefa pour limite0en+∞et on notelimx→+∞f(x) = 0sif(x)est aussi petit que l"on veut dès quexest assez grand ( Lorsqu"on dit petit, on sous-entend proche de zéro ). On définira de même :limx→-∞f(x) = 0.Exemple :limx→+∞1
x= 0;limx→+∞1x2= 0;limx→+∞1x3= 0;limx→+∞1⎷x= 0Exemple :limx→-∞1
x= 0;limx→-∞1x2= 0;limx→-∞1x3= 0Page 1/5
Année 2005-20061èreS
On peut à présent définir une limite quelconque en l"infini : Définition 3 :Soitfune fonction définieau moinssur un intervalle du type[a;+∞[: Avoirlimx→+∞f(x) =lest équivalent à avoirlimx→+∞[f(x)-l] = 0 Remarque :limx→+∞f(x) =l?f(x) =l+ε(x)aveclimx→+∞ε(x) = 0. -→démonstration Remarque :Une fonction n"a pas nécessairement de limite (finie ou infinie) lorsquextend vers fdéfinie surRparf(x) = cos(x)n"a de limite ni en-∞ni en+∞.II. Limite en un pointa
1) Limite en0
Définition 4 :Soitfune fonction définie au moins sur un intervalle ouvert en0: Sif(x)est aussi grand (positif) que l"on veut dès quexest assez proche de0, on dit quefa pour limite+∞en0et on notelimx→0f(x) = +∞. (On définit de mêmelimx→0f(x) =-∞.)Exemple :limx→01
x2= +∞limx→01⎷x= +∞. Remarque :Une fonction peut avoir une limite différente à gauche et à droite de0, on notera alors : lim x→0 x >01 x= +∞etlim x→0 x <01x=-∞ou encorelim x→0 x >01x3= +∞etlim x→0 x <01x3=-∞On note également parfois :lim
x→0+1 x3= +∞. Définition 5 :Soitfune fonction définie au moins sur un intervalle ouvert en0: Sif(x)est aussi petit que l"on veut (proche de0) dès quexest assez proche de0, on dit quefa pour limite0en0et on notelimx→0f(x) = 0. Exemple :limx→0x= 0;limx→0x2= 0;limx→0x3= 0;limx→0⎷ x= 0 Définition 6 :Soitfune fonction définie au moins sur un intervalle ouvert en0: On dit quefa pour limitelen0lorsque la fonctionx?→f(x)-la pour limite0 en0. Remarque :On peut traduire mathématiquement cette définition par lim x→0f(x) =l?limx→0?f(x)-l?= 0Page 2/5
Année 2005-20061èreS
2) Limites ena?R
Définition 7 :Soitfune fonction définie sur un intervalle ouvert ena, on dit quefa une limite enasi la fonctionh?→f(a+h)a une limite en0et alors : lim x→af(x) = limh→0f(a+h)Exemple :On alimx→1?
1 +1 (x-1)2? = lim h→0?1 +1h2?
Remarque :limx→af(x) =l?f(x) =l+ε(x)aveclimx→aε(x) = 0. Remarque :Sia?Dfet silimx→af(x)existe, alorslimx→af(x) =f(a).Exemple :Sia >0,limx→a⎷
x=⎷a.SiPest un polynôme,limx→aP(x) =P(a).
SiRest une fraction rationnelledéfinie ena,limx→aR(x) =R(a).III. Opérations sur les limites
Dans toute cettte partie les limites des fonctionsfetgsont??aux mêmes points??à savoir+∞, -∞oua?R.1) Somme
On a le tableau récapitulatif suivant :
limf(x) =lll+∞-∞+∞ limg(x) =l?+∞-∞+∞-∞-∞ lim?f(x) +g(x)?=l+l?+∞-∞+∞-∞F.I2) Produit
On a le tableau récapitulatif suivant :
limf(x) =ll >0l <0l >0l <0+∞-∞+∞0 limg(x) =l?+∞-∞+∞-∞-∞+∞ou-∞Page 3/5
Année 2005-20061èreS
3) Quotient
On a le tableau récapitulatif suivant :
limf(x) =+∞-∞±∞l <0ou-∞l >0ou+∞0 limg(x) =l?>0l?<0l?>0l?<0±∞0+0-0+0-0 lim?f(x)g(x)? Remarque :0+(resp.0+) indique que la limite est nulle et que la fonction reste positive (resp. négative). Il y a quatre formes indéterminées :+∞ - ∞;0× ∞;∞ ∞;00 Remarque :Avec ces régles de calcul et quelques transformations on peut trouver n"importe quelle limite. Exemple :On cherchelimx→+∞?x3-3x2+ 4x+ 1?. Si on voit ce polynôme comme une somme de monômes on obtient une F.I. du type +∞ - ∞mais on peut toujours écrirex3-3x2+ 4x+ 1 =x3? 1-3 x+4x2+1x3? aveclimx→+∞x3= +∞etlimx→+∞? 1-3 x+4x2+1x3? = 1-0 + 0 + 0 = 1par somme des limites. On a donc, par produit des limites,limx→+∞?x3-3x2+ 4x+ 1?= +∞vu comme??1×+∞??. -→A faire en TD : cas des polynômes et des fractions rationnelles.IV. Interprétation graphique et asymptotes
1) Asymptote horizontale
Silimx→+∞f(x) =l,
pourMetPles points d"abscissesx, lorsquexprend des valeurs de plus en plus grandes, la distancePMtend vers0:
On dit alors que la droiteDd"équationy=lest
asymptote horizontaleà la courbeCfau voisinage de+∞. Interprétation graphique pourlimx→-∞f(x) =l 01230 1 2 3 4 5 6 7 8
xyx lD Cf PMRemarque :On peut définir de même l"asymptote d"équationy=len-∞silimx→-∞f(x) =l
Page 4/5
Année 2005-20061èreS
2) Asymptote verticale
Silimx→af(x) =±∞,
on dit que la droiteDd"équationx=aest asymptote verticaleà la courbeCf. PetMsont ici les deux points de même ordonnée et la distancePMtend vers zéro lorsque cette ordonnée dePetMtend vers+∞. Interprétation graphique pourlimx→af(x) =-∞ 012340 1 2 3
xyaD CfP M
3) Asymptote oblique
Définition 8 :Soitfune fonction définie sur un intervalle du type[α;+∞[, s"il existe deux réelsa
etbtels quelimx→+∞[f(x)-(ax+b)] = 0on dira que la droiteDd"équationy=ax+b est asymptote obliqueàCfau voisinage de+∞. Remarque :La méthode de détermination est H.P. On a nécessairementlimx→+∞f(x) = +∞Interprétation graphique, avecPet
Mles deux points d"abscissesx, pour
limx→+∞[f(x)-(ax+b)] = 0 012340 1 2 3 4 5 6 7 8
xyxDCf
PMOn peut de même définir une asymptote oblique au voisinage de-∞silimx→-∞[f(x)-(ax+b)] = 0.
Page 5/5
quotesdbs_dbs2.pdfusesText_3[PDF] trouver les bons verbes en allemand
[PDF] trouver les cas latins par rapport aux mots suivants :
[PDF] trouver les composantes d'un vecteur dans une base
[PDF] trouver les contraires des mots
[PDF] trouver les coordonées d'un point d'un triangle dans un repère orthonormé
[PDF] Trouver les coordonnées d'un point de (d) et construire (d) [Theme vecteurs]
[PDF] Trouver les coordonnées d'un point grâce au vecteur
[PDF] Trouver les coordonnées d'un point par rapport ? sa symétrie
[PDF] Trouver les coordonnées d'un point sur une droite de fonction affine
[PDF] trouver les coordonnées d'un lieu
[PDF] trouver les coordonnées d'un point dans l'espace
[PDF] Trouver les coordonnées de D pour que ABCD sois un paralélogramme
[PDF] Trouver les coordonnées du point K tel que le quadrilatere ALBK soit un parallélogramme
[PDF] Trouver les définitions
