Exercices de mathématiques

Exercice 2. Méthode de la puissance a) Calculer les valeurs propres et les vecteurs propres de. A = ✓. 10 0. 9 1 ◇ . b) Que donne la méthode de la puissance

CORRECTION DU TD 3 Exercice 1

Pour conclure on étudie le sous-espace propre associé à la valeur propre en résolvant l'équation matricielle : . On a : Par conséquent

Exercices du chapitre 4 avec corrigé succinct

– Déterminer les valeurs propres et les vecteurs propres d'une matrice diagonale. 3. Montrer que : A non inversible ⇐⇒ 0 est valeur propre de A. Solution : 1.

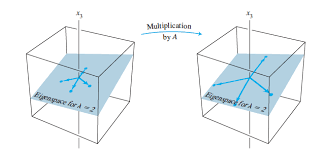Valeurs propres et vecteurs propres

Une telle solution est alors appelée vecteur propre associé à la valeur propre λ. Exercice. Montrer que 4 est une valeur propre de A = (. 0. −2.

Correction détaillée des exercices 12

https://licence-math.univ-lyon1.fr/lib/exe/fetch.php?media=a19:math3:correction-ex-3-4-maths3-2019.pdf

Exercice 1 Soit A = −1 2 3 0 −2 0 1 2 1 ∈ M3×3(R). Calculer le

Calculer les valeurs propres de T et donner une base de chaque espace propre. L'applica- tion T est-elle diagonalisable ? Corrigé. La première chose à faire

Leçon 05 – Exercices

A a trois valeurs propres distinctes donc A (ou f) est diagonalisable. V2 = (xy

Exercices de mathématiques - Exo7

Démontrer que 1 et 2 sont des valeurs propres de f. 2. Déterminer les vecteurs propres de f. 3. Soitu un vecteur propre de f pour la valeur propre 2. Trouver

Chapitre 9 — réduction des matrices et des endomorphismes

Soit λ une éventuelle valeur propre non nulle de f. Montrer alors l'égalité Eλ(f)=Eλ( ˜f). Solution de l'exercice 3. Corrigé en classe.

Exercices de mathématiques - Exo7

Déterminer les valeurs propres de M. 2. Montrer que M est diagonalisable. 3. Déterminer une base de vecteurs propres et P la matrice de passage. 4

Valeurs propres et vecteurs propres

appelée vecteur propre associé à la valeur propre ?. Exercice. Montrer que 4 est une valeur propre de A = (. 0. ?2. ?4. 2. ) et trouver les vecteurs.

Série dexercices no4/6 Recherche de valeurs propres Résolution

ATTENTION : une matrice réelle peut avoir des valeurs propres complexes. 4. Deux matrices A et B sont dites semblables s'il existe une matrice inversible P

Exercice 1 Soit A = ?1 2 3 0 ?2 0 1 2 1 ? M3×3(R). Calculer le

Calculer les valeurs propres de T et donner une base de chaque espace propre. L'applica- tion T est-elle diagonalisable ? Corrigé. La première chose à faire

Exercices du chapitre 4 avec corrigé succinct

– Déterminer les valeurs propres et les vecteurs propres d'une matrice diagonale. 3. Montrer que : A non inversible ?? 0 est valeur propre de A. Solution : 1.

Exercices de mathématiques - Exo7

Montrer que A et B n'ont pas de valeurs propres communes si et seulement si la matrice ?A(B) est inversible. Correction ?. [005678]. Exercice 29 **. Soit f un

Partiel Corrigé

7 nov. 2015 Correction: (exercice I) 1) Le polynome caractéristique vaut PA(x)=(x ... 2-iii) On a deux valeurs propres distinctes ±i en dimension 2 ...

ISCID-CO - PRÉPA 2ème année DIAGONALISATION Université du

3.5.4 Exercice récapitulatif (corrigé) . Cet exemple illustre un principe général concernant les valeurs propres d'une matrice diagonale.

Exercices de mathématiques - Exo7

Exercice 5. Soit A la matrice suivante. A = (1 1. 2 1. ) 1. Calculer le polynôme caractéristique et déterminer les valeurs propres de A.

Correction détaillée des exercices 12

http://licence-math.univ-lyon1.fr/lib/exe/fetch.php?media=a19:math3:correction-ex-3-4-maths3-2019.pdf

Enoncés et corrections : Sandra Delaunay

Exo7

Sujets de l"année 2004-2005

1 Devoir à la maison

Exercice 1SoitMla matrice réelle 33 suivante :

M=0 @0 21 32 0

2 2 11

A 1.

Déterminer les v aleurspropres de M.

Montrer que Mest diagonalisable.

3. Déterminer une base de v ecteurspropres et Pla matrice de passage. 4. On a D=P1MP, pourk2NexprimerMken fonction deDk, puis calculerMk. SoitEun espace vectoriel sur un corpsK(K=RouC), on appelleprojecteurun endomorphismepdeE vérifiantpp=p. Soitpun projecteur. 1.

Montrer que Id

Epest un projecteur, calculerp(IdEp)et(IdEp)p.

Montrer que pour tout ~x2Imp, on ap(~x) =~x.

3. En déduire que Im pet kerpsont supplémentaires. 4. Montrer quelerangdepestégalàlatracedep. (Onrappellequelatracedelamatriced"unendomorphisme ne dépend pas de la base dans laquelle on exprime cette matrice.)

SoitA=(aij)16i;j6nune matrice carréenn. On veut démontrer le résultat suivant dû à Hadamard : Supposons

que pour touti2 f1;;ng, on ait jaiij>nå j=1;j6=ijaijj alorsAest inversible. 1.

Montrer le résultat pour n=2.

2. Soit B, la matrice obtenue en remplaçant, pourj>2, chaque colonnecjdeApar la colonne c ja1ja 11c1;

Calculer lesbijen fonction desaij. Montrer que si les coefficients deAsatisfont les inégalités ci-dessus,

alors pouri>2, on a jbiij>nå j=2;j6=ijbijj: 1

3.Démontrer le résultat de Hadamard pour nquelconque.

Exercice 4Soit

A=0 @1 0 0 0 1 0 11 21 A Démontrer queAest diagonalisable et trouver une matricePtelle queP1APsoit diagonale. Soit A=0 @1 11 0 1 0

1 0 11

A Factoriser le polynôme caractéristique deA. La matriceAest-elle diagonalisable dansR? dansC? Soit A=a c c d

2M2(R)

Démontrer queAest diagonalisable dansR.

SoitAla matrice suivante

A=0 @0 1 1 1 0 1

1 1 01

CalculerA2et vérifier queA2=A+2I3. En déduire queAest inversible et donner son inverse en fonction de

SoitAune matrice carrée d"ordren. On suppose queAest inversible et quel2Rest une valeur propre deA.

Démontrer que l6=0.

Démontrer que si ~xest un vecteur propre deApour la valeur proprelalors il est vecteur propre deA1

de valeur proprel1. Soitfun endomorphisme deEvérifiantf2=mathrmIdE. 2

1.Démontrer que les seules v aleurspropres possibles de fsont 1 et1.

Vérifier que pour tout ~x2E, on a

f(~xf(~x)) =(~xf(~x))etf(~x+f(~x)) = (~x+f(~x)) et en déduire quefadmet toujours une valeur propre. 3. Démontrer que si 1 et 1 sont valeurs propres, alorsEest somme directe des sous-espaces propres correspondants. 4. T raduiregéométriquement sur un dessin dans le cas n=2. Exercice 10(9 points) SoitAla matrice deM3(R)suivante : A=0 @1 0 1 1 2 1 11 11 A 1. Démontrer que les v aleurspropres de Asont 1 et 2. 2. Déterminer les sous-espaces propres de A. La matriceAest-elle diagonalisable ? 3. Déterminer les sous-espaces caractéristiques de A. 4. Déterminer une base de R3dans laquelle la matrice de l"endomorphisme associé àAest B=0 @2 0 0 0 1 1

0 0 11

En déduire la décomposition de Dunford deB.

Résoudre le système dif férentiel

8>< :x 0=x+z y

0=x+2y+z

0=xy+z

(7 points) On considère la suite(un)n2Ndéfinie paru0=0,u1=1 et par la relation de récurrence

u n+1=12 (un+un1): 1. Déterminer une matrice A2M2(R)telle que pour toutn>1 on ait un+1 u n =Anu1 u 0

Justifier.

2.Déterminer le polynôme caractéristique PA(X)deAet calculer ses racinesl1etl2.

3. Soit Rn(X) =anX+bnle reste de la division euclidienne deXnparPA(X). Calculeranetbn(on pourra utiliser les racinesl1etl2). 4. Montrer que An=anA+bnI2, en déduire que la matriceAnconverge lorsquentend vers+¥vers une limiteA¥que l"on déterminera. Calculer limn!+¥un. (5 points) SoitAune matrice carrée,A2Mn(K)(K=RouC). On rappelle que la trace d"une matrice est la somme de ses coefficients diagonaux et que tr(BAB1) =trA. Démontrer que det(expA) =etrAdans les cas suivants :

1.Adiagonalisable.

2.Atriangulaire supérieure ayant une diagonale de zéros.

3.Atrigonalisable.

4.Aquelconque.

Exercice 13(7 points) On considère la suite(un)n2Ndéfinie paru0=0,u1=1 et par la relation de récurrence

u n+1=12 (un+un1): 1. Déterminer une matrice A2M2(R)telle que pour toutn>1 on ait un+1 u n =Anu1 u 0

Justifier.

2. Déterminer le polynôme caractéristique PA(X)deAet calculer ses racinesl1etl2. 3. Soit Rn(X) =anX+bnle reste de la division euclidienne deXnparPA(X). Calculeranetbn(on pourra utiliser les racinesl1etl2). 4. Montrer que An=anA+bnI2, en déduire que la matriceAnconverge lorsquentend vers+¥vers une limiteA¥que l"on déterminera. Calculer limn!+¥un. (5 points) SoitAune matrice carrée,A2Mn(K)(K=RouC). On rappelle que la trace d"une matrice est la somme de ses coefficients diagonaux et que tr(BAB1) =trA. Démontrer que det(expA) =etrAdans les cas suivants :

1.Adiagonalisable.

2.Atriangulaire supérieure ayant une diagonale de zéros.

3.Atrigonalisable.

4.Aquelconque.

(4 points) On suppose qu"une populationxde lapins et une populationyde loups sont gouvernées par le système

suivant d"équations différentielles : (S)(x0=4x2y y 0=x+y 1.

Diagonaliser la matrice

A=42 1 1 2. Exprimer le système (S)et ses solutions dans une base de vecteurs propres deA. 3. Représenter graphiquement les trajectoires de (S)dans le repère(Oxy). 4.

Discuter graphiquement l"év olutionde la population des lapins en fonction des conditions initiales.

(9 points) Soitul"endomorphisme deR3, dont la matrice dans la base canonique est A=0 @3 22 1 0 1

1 1 01

A 1. Calculer les v aleurspropres de A. L"endomorphismeuest-il diagonalisable ? 2. Calculer (AI)2. Montrer queAn=nA+(1n)Ien utilisant la formule du binôme de Newton. 3. Soient P(X) = (X1)2etQ2R[X]. Exprimer le reste de la division euclidienne deQparPen fonction

deQ(1)etQ0(1), oùQ0est le polynôme dérivé deQ. En remarquant queP(A) =0 et en utilisant le

résultat précédent avec un choix judicieux du polynômeQ, retrouverAn. 4. (a) Montrer que l"image de R3par l"endomorphismeuId est un sous-espace vectoriel de dimension

1, on noterae2une base.

quotesdbs_dbs4.pdfusesText_7

[PDF] Exercices de mathématiques - Exo7

Enoncés et corrections : Sandra Delaunay

Sujets de l"année 2004-2005

1 Devoir à la maison

Exercice 1SoitMla matrice réelle 33 suivante :

2 2 11

Déterminer les v aleurspropres de M.

Montrer que Mest diagonalisable.

Montrer que Id

Epest un projecteur, calculerp(IdEp)et(IdEp)p.

Montrer que pour tout ~x2Imp, on ap(~x) =~x.

Montrer le résultat pour n=2.

3.Démontrer le résultat de Hadamard pour nquelconque.

Exercice 4Soit

1 0 11

2M2(R)

Démontrer queAest diagonalisable dansR.

SoitAla matrice suivante

1 1 01

Démontrer que l6=0.

1.Démontrer que les seules v aleurspropres possibles de fsont 1 et1.

Vérifier que pour tout ~x2E, on a

0 0 11

En déduire la décomposition de Dunford deB.

Résoudre le système dif férentiel

0=x+2y+z

0=xy+z

Justifier.

2.Déterminer le polynôme caractéristique PA(X)deAet calculer ses racinesl1etl2.

1.Adiagonalisable.

2.Atriangulaire supérieure ayant une diagonale de zéros.

3.Atrigonalisable.

4.Aquelconque.

Justifier.

1.Adiagonalisable.

2.Atriangulaire supérieure ayant une diagonale de zéros.

3.Atrigonalisable.

4.Aquelconque.

Diagonaliser la matrice

1 1 01

1, on noterae2une base.