 REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
Déterminer les coordonnées du point d'intersection de la droite ( ) avec le plan de repère. ( ; ⃗ ⃗). Page 2. Yvan Monka – Académie de Strasbourg –
 Méthodes de géométrie dans lespace Déterminer une équation
Méthodes de géométrie dans lespace Déterminer une équation
L'équation cartésienne d'un plan est du type ax + by + cz + d = 0 avec (a ;b ;c) les coordonnées d'un vecteur normal du plan . On procède en deux étapes : D'
 fic00159.pdf
fic00159.pdf
Donner un vecteur directeur la pente une équation paramétrique et une équation cartésienne des droites équation du plan est ax+by+cz+d = 0. On trouve : i ...
 Chapitre 14 : Equations paramétriques et cartésiennes
Chapitre 14 : Equations paramétriques et cartésiennes
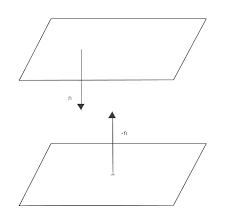
Remarques 4 : Deux plans orthogonaux à une même droite sont parallèles entre eux. Remarques 5 : Deux droites orthogonales à un même plan sont parallèles entre
 Sans titre
Sans titre
Déterminer une équation cartésienne du plan (P) passant par le point C(1 -1
 1 Passer des équations paramétriques `a léqua- tion cartésienne d
1 Passer des équations paramétriques `a léqua- tion cartésienne d
o`u les deux vecteurs V = (αβ
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
est une équation cartésienne de la droite (AB). Equations cartésiennes d'un plan : On se place dans l'espace muni d'un repère orthonormé . Soient
 Equations de sous-espaces vectoriels
Equations de sous-espaces vectoriels
27 févr. 2013 Idée : Eliminer les paramètres d'une équation paramétrique c'est ... 2 Dans R3 muni de sa base canonique
 Représentations paramétriques et équations cartésiennes Fiche
Représentations paramétriques et équations cartésiennes Fiche
La droite D passe par le point A (1 2
 REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
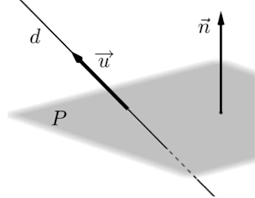
1) Démontrer que la droite ( ) et le plan P sont sécants. 2) Déterminer leur point d'intersection. 1) Un vecteur normal de P est 7? ^. 2.
 Méthodes de géométrie dans lespace Déterminer une équation
Méthodes de géométrie dans lespace Déterminer une équation
L'équation cartésienne d'un plan est du type ax + by + cz + d = 0 avec (a ;b ;c) les coordonnées d'un vecteur normal du plan . On procède en deux étapes : D'
 Représentation paramétrique de droites de plans Applications
Représentation paramétrique de droites de plans Applications
Définition : On appelle représentation paramétrique ou système d'équations paramétriques de la droite. D par un point A (xA ; yA ; zA) et de vecteur
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Soit P un plan muni d'un repère R(Oi
 Géométrie affine en dimension 3
Géométrie affine en dimension 3
Représentations paramétriques d'une droite ou d'un plan . . . . . . . . . 5. II.2. Équations cartésiennes Équations cartésiennes d'une droite affine .
 1 Passer des équations paramétriques `a léqua- tion cartésienne d
1 Passer des équations paramétriques `a léqua- tion cartésienne d
o`u les deux vecteurs V = (??
 Aix-Marseille Université - Géométrie et arithmétique 1
Aix-Marseille Université - Géométrie et arithmétique 1
9 oct. 2015 et C (41) trois points du plan. 1. Donner une équation paramétrique de la médiatrice mAB du segment [AB]. La mediatrice est la droite par le ...
 VECTEURS ET DROITES
VECTEURS ET DROITES
D est une droite du plan. On appelle vecteur directeur de D tout vecteur non nul u ! qui possède la même direction que la droite D. 2) Equation cartésienne
 Mathématiques générales I
Mathématiques générales I
2 EQUATION D'UNE DROITE DANS LE PLAN. GEOMETRIE EUCLIDIENNE – 6 comme équation cartésienne alors v(a
 PRODUIT SCALAIRE DANS LESPACE
PRODUIT SCALAIRE DANS LESPACE
2) Equation cartésienne d'un plan. Théorème : L'espace est muni d'un repère orthonormé . Un plan P de vecteur normal non nul admet une équation cartésienne de
 REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS
>REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS WebDans un repère orthonormé les plans P et P' ont pour équations respectives : 2 +4/+40?3=0 et 2 ?5/+40?1=0 Démontrer que les plans P et P' sont perpendiculaires
 Chapitre 14 : Equations paramétriques et cartésiennes
Chapitre 14 : Equations paramétriques et cartésiennes
>Chapitre 14 : Equations paramétriques et cartésiennesWebReprésentation paramétrique d’un plan Dans l’espace muni d’un repère on considère le plan (passant par le point 0; 0; 0)et dirigé par les vecteurs directeurs ??( ) et ?( ? ? ?) où ( ; ;
 Géométrie dans l’espace
Géométrie dans l’espace
>Géométrie dans l’espace
 Exercices corrigés PROF: ATMANI NAJIB
Exercices corrigés PROF: ATMANI NAJIB
>Exercices corrigés PROF: ATMANI NAJIB
 Déterminer des équations vectorielle paramétriques et
Déterminer des équations vectorielle paramétriques et
>Déterminer des équations vectorielle paramétriques et WebDéterminer des équations vectorielle paramétriques et cartésienne d'un plan Exemple 1 On considère le plan ABC comprenant les points A: (-3 2 0) B: (1 1 1) et C: (0 4
Comment définir une équation paramétrique ?
Une équation paramétrique de la droite (d) passant par le point A (1 ; 2 ; 3) et de vecteur directeur (-1 ; 2 ; 1) est avec t ? . 2. Représentation paramétrique d'un plan a. Généralités La donnée de deux vecteurs et non colinéaires et d'un point A permet de définir entièrement un plan.
Comment convertir les équations d'un plan en forme paramétrique ?
calculatrice pour convertir les équations d'un plan en forme paramétrique, cartésienne canonique et cartésienne avec le vecteur normal. Entrez l'une des trois équations d'un plan. Mathepower calcule les autres deux. Choisissez comment le plan doit être donné.
Comment calculer l’équation du plan?
D’après l’équation de P, on peut prendre comme vecteur normal~n(2;?1;3). On a alors pour un point M de (Q): ??? AM ·~n=0 2(x?3)?(y+1)+3(z?0) 2x?y+3z?6?1 =0 2x?y+3z?7 =0 Conclusion : une équation du plan (Q)est : 2x?3y?z?7 =0.
Représentation paramétrique
de droites, de plansApplications
Christophe ROSSIGNOL
Année scolaire 2019/2020Table des matières
1 Représentations paramétriques
21.1 Définition
21.2 Intersection de deux droites
22 Représentation paramétrique d"un plan de l"Espace
4Table des figures
Liste des tableaux
1 Positions relatives de deux droites
52 Positions relatives d"une droite et d"un plan
53 Positions relatives de deux plans
5Ce cours est placé sous licence Creative Commons BY-SAhttp://creativecommons.org/licenses/by-sa/2.0/fr/
11 REPRÉSENTATIONS PARAMÉTRIQUES
1 Représentations paramétriques d"une droite de l"Espace
1.1 Définition
On se place dans un repère
O;!{;!|;!k
de l"Espace. SoitDune droite passant par un pointA(xA;yA;zA)et de vecteurdirecteur!u0 @a b c1 A M(x;y;z)est un point deDsi et seulement si il existe un réelttel que!AM=t!u.En passant aux coordonnées, on obtient :
8>< :xxA=at yyA=bt zzA=ctc"est-à-dire8 :x=xA+at y=yA+btz=zA+ctDéfinition :On appellereprésen tationparamétrique ou système d"équations paramétriques de la droite
Dpar un pointA(xA;yA;zA)et de vecteur directeur!u0 @a b c1 A le système : 8 :x=xA+at y=yA+bt z=zA+ctavect2RLe réeltest appelép aramètre.Remarques :1.Un p ointMest surDsi et seulement si il existe un réelttel que les coordonnées deM
vérifie le système d"équations paramétriques deD. 2. Récipro quement,si la droite admet comme équation paramétrique8 :x=x0+t y=y0+t z=z0+ t, cette droite passe par le pointM0(x0;y0;z0)et admet comme vecteur directeur!v0 1 A 3.P ourobtenir une représen tationparamétrique d usegmen t[AB], il suffit de prendre comme vecteur
directeur!AB, comme point de la droite le pointAet de prendret2[0; 1]. 4.P ourobtenir une représen tationparamétrique de la demi-droite [AB), il suffit de prendre comme
vecteur directeur!AB, comme point de la droite le pointAet de prendret2[0; +1[. Exercices :16, 18, 19 page 299 et 86, 87 page 3101- 107 page 3142- 115 page 3163- 119, 120, 121 page 3164[TransMath]
1.2 Intersection de deux droites
Les résultats concernant les positions relatives de deux droites de l"Espace sont rappelées dans le tableau
1 Remarque :Dest une droite de vecteur directeur!uetest une droite de vecteur directeur!v.Si !uet!vsont colinéaires :
Si Detn"ont pas de point commun, elles sont strictement parallèles; Si Detont un point commun, elles sont confondues.1. Représentation paramétrique d"une droite.2. Type BAC.
3. Points équidistants de trois points.
4. Segments, demi-droites.
21 REPRÉSENTATIONS PARAMÉTRIQUES 1.2 Intersection de deux droites
Si !uet!vne sont pas colinéaires : Si Detn"ont pas de point commun, elles sont non coplanaires; Si Detont un point commun, elles sont sécantes. %Exercice résolu :Dans un repèreO;!{;!|;!k
de l"Espace, on considère les droitesD1,D2etD3 de représentations paramétriques : D 1:8 :x=1 + 2t y= 4t z= 53tt2RD2:8 :x=6t+ 8 y=12t+ 1 z= 9t2t2RD3:8 :x=t+ 6 y= 3t1 z=2t+ 2t2RÉtudier les positions relatives deD1etD2puis deD1etD3.Positions relatives deD1etD2:Un vecteur directeur deD1est!u0
@2 4 31A et un vecteur directeur deD2est!v0 @6 12 91
A On a !v=3!u. Les vecteurs!uet!vsont colinéaires donc les droitesD1etD2sontparallèles. Reste à déterminer si les deux droites sontstrictement parallèlesouconfondues.
Le pointA(1; 0;5)est un point deD1.
A2 D2()8
:6t+ 8 =112t+ 1 = 0
9t2 = 5()8
:t=32 t=112 t=79Ce qui est impossible. Par suite,A =2 D2.
Les droitesD1etD2sont doncstrictement parallèles. Positions relatives deD1etD3:Un vecteur directeur deD1est!u0 @2 4 31A et un vecteur directeur deD3est!w0 @1 3 21
A
Les vecteurs
!uet!wne sont pas colinéaires donc les droitesD1etD3sont soitsécantes, soitnon coplanaires. On va donc chercher un éventuel point d"intersection àD1etD3. M(x;y;z)2 D1\ D3()il existe deux réelstetstels que8 :x=1 + 2t y= 4t z= 53tet8 :x=s+ 6 y= 3s1 z=2s+ 2On a donc :
8>< :1 + 2t=s+ 64t= 3s1
53t=2s+ 2()8
:s= 2t74t= 3(2t7)1
53t=2(2t7) + 2()8
:s= 2t74t= 6t22
53t=4t+ 16()8
:s= 15 t= 11 t= 11 Les droitesD1etD3sont doncsécanteset leur point d"intersection a comme coordonnées : 8>< :x=1 + 211 = 21 y= 411 = 44 z= 5311 =28 3RÉFÉRENCES
Remarques :1.A ttention!Lors de la rec herched"un év entuelp ointd" intersectionen tredeux droites, il
fautabsolumentdonner deux noms différents aux deux paramètres. 2.Si les droites a vaientété non coplanaires, on aurait, lors de la résolution du système, trouv édeu x
valeurs différentes pourt(ous), ce qui est impossible. Exercices :20, 21, 22, 23 page 300; 90 page 310 et 92, 93 page 3115- 108, 109 page 3146[TransMath]2 Représentation paramétrique d"un plan de l"Espace
Un planPest caractérisé par la donnée d"un pointA(x0;y0;z0)et de deux vecteurs directeurs~u0
@a b c1 A et ~v 0 @a0 b 0 c 01 A non colinéairesM(x;y;z)2 P ()!AM,!uet!vcoplanaires
!AM=t~u+t0~v, avect;t02R ()8 :xx0=at+a0t0 yy0=bt+b0t0 zz0=ct+c0t0; t;t 02R 8 :x=x0+at+a0t0 y=y0+bt+b0t0 z=z0+ct+c0t0; t;t 02RLe système obtenu est appelé
représen tationparamétrique du plan P.On peut utiliser cette représentation paramétrique pour étudier les positions relatives d"une droite et d"un plan
(voir tableau 2 ) ou de deux plans (voir tableau 3Remarque :Il existe un moyen plus simple d"étudier ces positions relatives. il sera vu dans le chapitre
" Orthogonalité, produit scalaire » et fait intervenir les équations de plans.Exercices :94, 95, 96, 97 page 311[TransMath]
Références
[TransMath]quotesdbs_dbs9.pdfusesText_15[PDF] equation projectile avec frottement
[PDF] equation quotient seconde
[PDF] equation signal dent de scie
[PDF] équation simple valeur absolue
[PDF] équation symétrique
[PDF] équation tendance linéaire
[PDF] equation trigonometrique avec cos et sin
[PDF] equation valeur absolue exercice
[PDF] équation vectorielle d'une droite dans l'espace
[PDF] équations aux dérivées partielles cours
[PDF] équations aux dérivées partielles linéaires du premier ordre
[PDF] equations différentielles ordinaires exercices corrigés
[PDF] equations differentielles premier ordre
[PDF] equations differentielles resumé
