 Constructions à la règle et au compas
Constructions à la règle et au compas
triangle équilatéral inscrit dans le même cercle. P. O. Il est facile aussi
 VErS UNE éVolUtioN dE la ViSioN EN GéoMétriE aU PriMairE
VErS UNE éVolUtioN dE la ViSioN EN GéoMétriE aU PriMairE
Les chemins que nous avons choisis sont des objets géométriques : la droite le segment
 La traduction latine des Éléments dEuclide par Federico
La traduction latine des Éléments dEuclide par Federico
3 sept. 2021 11-38 ; Veronica Gavagna « La tradizione euclidea nel Rinascimento » in ibidem
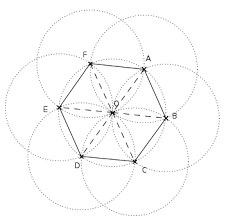 Ch 8 Sommaire 0- Objectifs CERCLE ET POLYGONE RÉGULIER
Ch 8 Sommaire 0- Objectifs CERCLE ET POLYGONE RÉGULIER
En traçant deux diamètres perpendiculaires on obtient un carré. Puis avec BDF est un triangle équilatéral inscrit dans un cercle de centre O donc FOB ...
 LA GÉOMÉTRIE IMAGINAIRE ET LA NOTION DESPACE
LA GÉOMÉTRIE IMAGINAIRE ET LA NOTION DESPACE
bien convexe par rapport à un côté déterminé de la figure. Si le rayon R se présente comme infini il n'y a pas en réalité de cercle osculateur. C'est alors
 Mise en page 1
Mise en page 1
Inscrire un triangle équilatéral dans un cercle de centre donné (6E). 1 https://www.euclidea.xyz/. − −. = x y. 11 5 45 0 (2). = −......
 Untitled
Untitled
carré gris du motif 4 (un carré ayant 4 carreaux gris de côté) ? 2) a ... centre du cercle inscrit au triangle. A. B. C. A. B. C. A. B. C. A. B. C. A. B. C.
 Le cercle au collège
Le cercle au collège
20 mars 2008 Cercle et carré. 5 Triangle isocèle. 6. Projection de deux points d'un ... L'angle EDF inscrit dans le demi-cercle de diamètre [EF] est droit ...
 La traduction latine des Éléments dEuclide par Federico
La traduction latine des Éléments dEuclide par Federico
18 sept. 2021 11-38 ; Veronica Gavagna « La tradizione euclidea nel Rinascimento » in ibidem
 octobre 1999
octobre 1999
1 oct. 1999 aire que le carré inscrit; tandis que celles de la fig. 3.b) ont la ... cercle se métamorphose en une figure géo- métrique facilement ...
 Le Jeu de Platon Constructibilité à la règle non graduée et au compas
Le Jeu de Platon Constructibilité à la règle non graduée et au compas
non graduée et au compas un carré d'aire double d'un carré donné. équivalent à tracer un polygone régulier à n côtés inscrit dans un cercle donné.
 Constructions à la règle et au compas
Constructions à la règle et au compas
Un compas est un instrument de géométrie qui sert à tracer des cercles ou des arcs Il est facile aussi
 CONSTRUIRE UN PARALLÉLOGRAMME Méthode 1 : en traçant
CONSTRUIRE UN PARALLÉLOGRAMME Méthode 1 : en traçant
rayon BC. ? On trace un arc de cercle de centre C et de rayon AB. ? On nomme D le point d'intersection des deux. Arcs de cercle tracés.
 Module 7. Angle inscrit et angle au centre
Module 7. Angle inscrit et angle au centre
Durant la septième année le cercle a été réétudié pour travailler avec ses éléments et déterminer la signification de la tangente à la circonférence et déduire
 Ce sujet vise à évaluer des connaissances géométriques
Ce sujet vise à évaluer des connaissances géométriques
cercle a) Réaliser la figure en suivant la consigne donnée. (carré losange
 25e RMT FINALE mai 2017 Titre Catégorie Origine Domaines
25e RMT FINALE mai 2017 Titre Catégorie Origine Domaines
À partir de 29 segments isométriques construire un assemblage de carrés qui le carré est sur les vues a) et c)
 Symétrie centrale - Exercices
Symétrie centrale - Exercices
Un carré d. Un triangle isocèle e. Un triangle équilatéral f. Un cercle. Page 2
 Outils pour les maths - CM1
Outils pour les maths - CM1
a. La figure est formée d'un carré avec ses diagonales. Dans le carré il y a un cercle dont le centre est l'intersection des diagonales.
 Comptes Rendus Mathématique
Comptes Rendus Mathématique
21 juil. 2021 2Un triangle est inscrit dans un cercle si le cercle passe par ses sommets. Dans ce cas le cercle est dit circonscrit au.
 1 Chapitre I : Geometrie classique
1 Chapitre I : Geometrie classique
Application : On peut construire a la regle et au compas des racine carre arbitraire. Rappel : Cercle inscrit et circonscrit d'un triangle :.
 Géométrie euclidienne dans le plan
Géométrie euclidienne dans le plan
Cercle : Uncercleestl’ensembledespointséquidistantsd’uncentre UncercleCestalors dé?ni par son centre et son rayon Dans un cercle : • Ladroitequicoupeuncercleenunseulpointestune tangente (T) Cette tangente est orthogonale au rayon • l’angle au centre vaut deux fois l’angle inscrit : ? “ 2?
 un carre dans un cercle - ac-noumeanc
un carre dans un cercle - ac-noumeanc
donc OG= r 2 c’est le côté d’un carré inscrit dans le cercle de rayon r Cette méthode permet de construire un carré inscrit dans un cercle uniquement avec le compas
Quelle est la constante du cercle ?
Première approximation satisfaisante, donnée par Archimède, de la constante du cercle. Depuis l’apparition des ordinateurs les décimales de?s’enchaînent à un rythme de plusen plus rapide. Le record fut établi en 2011 par deux japonaisavec plus de 10 000 milliardsde décimales après 371 jours de travail.
Qu'est-ce que la géométrie euclidienne ?
Les ?gures de base en géométrie euclidienne sont les quadrilatères et les triangles qui sonttrès riches en propriétés (parallélisme, orthogonalité, longueur, symétrie) et permettentainsi la construction à la règle et au compas et de montrer de nouvelles propriétés. Quadrilatère donc les côtes opposés sont deux à deux parallèles.
Quelle est la différence entre un cercle et un bac ?
BAC: correspond à l’anglerentrant(compris entre 180? et 360?). Cercle : ~ Un cercle est l’ensemble des points équidistants d’un centre. UncercleCest alorsdé?ni par son centre et son rayon. La droite qui coupe un cercle en un seul point est unetangente(T). Cette tangente est orthogonale au rayon.
Qu'est-ce que la tangente euclidienne ?
Cette tangente est orthogonale au rayon. Les ?gures de base en géométrie euclidienne sont les quadrilatères et les triangles qui sonttrès riches en propriétés (parallélisme, orthogonalité, longueur, symétrie) et permettentainsi la construction à la règle et au compas et de montrer de nouvelles propriétés.
Constructions à la règle et au compas
FrançoisDEMARÇAY
Département de Mathématiques d"Orsay
Université Paris-Sud, France
C"est au cours d"une méditation que je découvre cette chose - évidente à vrai dire pour peu qu"on se pose la question - que dans ma démarche spontanée à la découverte des choses, que ce soit en mathématiques ou ailleurs, le "ton de base» est "yin», "féminin», et aussi et surtout, que contrairement à ce qui se passe le plussouvent, je suis resté fidèle à cette nature originelle en moi, sans jamais l"infléchir ou
la corriger pour me conformer aux valeurs dominantes en honneur dans les milieux environnants. AlexandreGROTHENDIECKy1.Compas celtes (gaulois)
L"archéologie démontre qu"à partir du V
èmesiècle avant Jésus-Christ, l"art celtique acommencé à élaborer des instruments de précision pour dessiner des décors géométriques,
architecturaux, artistiques.Lespremières"machinesàtracerdescercles»ontdisparu,etellesétaientprobablement
fabriquées en bois.Mais certains compas
1métalliques gaulois "à pas variables» se sont conservés. Voici
l"un d"entre eux, retrouvé sur le site de l"Oppidum de Bibracte2. Jambes mobiles, écartement variable : le principe n"a pas évolué depuis plus de deuxmille cinq cent ans!1. Le terme est undéverbal-on prend le verbe, et on enlève le caractère verbal - decompasser, lui-
même issu du bas latincompassaresignifiantmesurer avec le pas, qui s"est spécialisé dans le sens actuel dès
le XIIèmesiècle.
2. La ville de Bibracte était la capitale desÉduens, peuple celte (gaulois) qui a connu son apogée au Ier
siècle avant Jésus-Christ. Centre névralgique du pouvoir de l"aristocratie éduenne, Bibracte fut aussi un lieu
d"artisanat et de commerce où se côtoyaient mineurs, forgerons, frappeurs de monnaie. Au sommet duMont Beuvraydans le Massif du Morvan, à 850 m d"altitude, cette métropole disparueétait situé sur le territoire actuel des communes de Saint-Léger-sous-Beuvray (Saône-et-Loire), de Glux-en-
Glenne et de Larochemillay (Nièvre).
12 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Les compas deviennent abondants dans les fouilles archéologiques à partir de la fin du
II èmeavant Jésus-Christ.Déjà au tout début de l"âge du Fer, à savoir aux Vèmeet IVèmesiècles avant J.-C., on
trouve des motifs circulaires très raffinés, notamment sur des vases en céramique, sur dessculptures en os, sur des fourreaux d"épé en fer, sur des coupes à boire en or, sur des pièces
de harnachement en bronze. Rosaces, croissants, amandes, pétales, lunules, enchevêtrements élégants d"arcs decercles : l"art de prestige fourmille de réussites esthétiques.Comme le laisse deviner le raffinement de phalères
3en bronze ajouré remarquablement
conservées, certaines figures géométriques ne peuvent avoir été construites que sur des
bases mathématiques extrêmement bien maîtrisées.Depuis le 25 septembre 1984, le site héberge leMusée de la civilisation celtique, lequel retrace la vie de
cette cité de quelque 5 à 10 milliers d"âmes au sein d"un oppidum fortifié que les fouilles archéologiques du
mont Beuvray ont révélé peu à peu.3. Dans l"Antiquité romaine, lesphalèresétaient des plaques métalliques brillantes utilisées comme
ornement (signets d"un casque, par exemple).2. Compas divers 3
Les archéologues ont pu démontrer que le découpage d"un cercle ennparties égales, pourn= 3;4;5;15, était généralement maîtrisé par les artistes celtes. Mais relativement peu de motifs polygonaux à six côtés réguliers (hexagonaux) semblent avoir existé, probablement parce qu"ils étaient trop simples à réaliser.C"est le motif pentagonal régulier (cinq côtés), qui témoignait de la valeur de l"artiste,
en raison de la difficulté relative d"exécution. Comme exemple de l"excellence de l"art dès le Vèmesiècle avant J.-C., citons la phalère
de Somme-Bionne sur-Retourne qui présente 9 demi-cercles, et dont le décor a nécessité le
tracé de 120 cercles, ainsi que la phalère de Cuperly, qui a demandé 193 cercles de 8 à 10
rayons différents, soit 180 coups de compas!Si l"utilisation du compas est flagrante dans l"art décoratif, il peut aussi, mais plus rare-
ment, s"illustrer dans l"architecture, bien que de moindre valeur d"apparât. Le bassin monumental de Bibracte en est un exemple.2.Compas divers
Un compas est un instrument de géométrie qui sert à tracer des cercles ou des arcs decercle, mais aussi à comparer, à reporter ou à mesurer des distances. Il est constitué de
deux branches jointes par une articulation. Les compas sont, ou ont été, utilisés en mathé-
matiques, en architecture, en dessin industriel, en géographie. Les Grecs attribuaient son invention à Talos, le neveu de Dédale.4 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Dans l"inconographie, le compas est un instrument de mesure du monde, témoin d"une
concentration mathématique avisée.3.Prologue sur les constructions à la règle et au compas
et sur les problèmes impossiblesSi l"on souhaite réussir à enseigner de bellesMathématiques à l"Écoleavec une élégance
proche de celle des Grecs, il importe de soigner, face à un public d"enfants attentifs et curieux, l"aspectdynamique et esthétiquedes constructions géométriques. Les constructions de géométrie dans le plan trouvent leurs racines dans la haute Anti-quité, et elles ont connu un essor spectaculaire dans les mathématiques grecques.Les constructions à la règle et au compas occupent une place considérable dans lesÉlé-
ments d"Euclide. Pour les mathématiciens Grecs, les cercles et les droites sont des figuresidéales, puisqu"en elles, tous les défauts et toutes les impuretés de leurs réalisations phy-
siques - dans le sable, au tableau, sur un papyrus - ont disparu.3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 5
Presque tous les problèmes de construction géométrique à la règle et au compas que l"on
sait résoudre aujourd"hui étaient déjà parfaitement maîtrisés par les Grecs.Euclide a fondé sa géométrie sur un système d"axiomes qui assure en particulier qu"il est
toujours possible de tracer une droite passant par deux points donnés et qu"il est toujours possible de tracer un cercle de centre donné et passant par un point donné.La géométried"Euclide est donc la géométrie des droites et des cercles, tracés à la règle et au compas.
L"intuition (conjecturale) d"Euclide était que tout point géométrique pouvait être construit,
ou "obtenu», à l"aide de ces deux instruments. En particulier, tout "nombre» devait pou- voir être accessible comme grandeur géométrique constructible. Mais une telle conjecture fondée sur une croyance intuitive en la puissance des objetsgéométriques avait déjà été remise en question chez les Grecs. On savait en effet depuis
l"École de Pythagore que les nombres rationnels ne suffisent pas à exprimer toutes les lon-gueurs géométriques, puisque la diagonale d"un carré de côté1, qui correspond au nombrep2, ne peut jamais s"exprimer comme une fractionpq
avec deux entiers non nulsp;q2N.Rappelons en effet :
Théorème 3.1.Le nombre :p2 = 1;414213562373095048801689 n"est pas rationnel, à savoir plus précisément, pour tous entiersp; q2N, on a :p26=pqDémonstration.Ce théorème bien connu et considéré comme très élémentaire par les ma-
thématiciens contemporains est en fait beaucoup plus subtil, complexe et puissant qu"il semble en avoir l"air. En effet, il affirme que dans l"univers extrêmement grand de toutes les fractions ration- nelles pq , aucune ne donne la valeur exacte dep2. Ceci est quelque peu contre-intuitif, car l"on sait que les fractions rationnelles, avec de grands nombres entiers, peuvent approximer tout nombre réel à un nombre quelconque de décimales près. Voici par exemple le développement décimal d"une fraction rationnelle de taille pas si modeste que cela :1234567823456789 = 0;5263157715:Et d"ailleurs, si l"on veut par exemple capturer les 15 première décimales de :p2 =1;414213562373095048801689;
il suffit évidemment de choisir la fraction : pq :=14142135623730951000000000000000 La force du théorème, c"est que quelle que soit la complexité de deux entiersp; q2N, on ne pourra jamais capturer avec pq toutesles décimales dep2jusqu"à l"infini! Pour démontrer cela, supposons au contraire, en raisonnant par contradiction, qu"il soit possible de représenter :p2 = pq Rappelons qu"un nombre entierr2Nquelconque est toujours soit pair, soit impair.6 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Nombres pairs
Nombres impairs
111013129678 54321
On peut écrire cela sous forme d"une réunion disjointe : N =2N[2N+ 1: Par définition,être pair, c"est être multiple de2. Tout nombre pairr22Nest donc de la forme : r= 2r0; avecr02N. Mais à nouveau,r0est ou bien pair ou bien impair. Lorsquer0est pair, onécrit :
r0= 2r00;
d"où : r= 2r0= 22r00= 22r00: Par récurrence, on se convainc aisément que la chasse à la présence d"un facteur2doit se terminer, et donc, que tout nombrer2Ns"écrit de manière unique comme : r= 2ar; avec un certain entier-exposanta>0et avec un certain reste-facteurr22N+ 1qui est impair. Alors en revenant à la question de savoir si l"on peut écrirep2 = pq , décomposons de la sorte : p= 2apetq= 2bq; aveca;b>0et avec deux restes-facteursimpairsp;q22N+ 1. Par règle de simplification des fractions, lorsquea>b, on peut écrire : pq =2ap 2 bq =2abp q =nouveaupnouveauqimpair; et de même lorsqueb>a: pq =2ap 2 bq =p 2 baq =nouveaupimpairnouveauq: En résumé, nous avons donc montré que si jamais l"on pouvait écrire p2 = pq sous fraction :p2 = p0q 0; dont les deux nouveaux élémentsp0etq0ne sont pas tous les deux des nombres pairs: au moins l"un d"eux est impair.3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 7
Et c"est là que tout va se "casser la gueule», puisqu"en élevant au carré : 2 = p02q 02; puis en chassant le dénominateur :2q02=p02;
on obtient une identité montrant quep02estpair. Or on se souvient par réminiscence arith- méticienne que tout nombreimpair1 + 2rpossède un carré qui estaussiimpair :1 + 2r2= 1 + 4r+ 22r2|{z}
pair!; donc sip02est pair, c"est quep0lui-mêmedoitêtre pair : p0= 2p00:
Mais alors l"identité laissée en chemin devient :2q02=2p002;
ce qui, après division par2, fournit une identité : q02= 2p002;
qui montre queq0doit lui aussi être pair! Nous débouchons donc malencontreusement sur la conséquence quep0est pair et queq0 est lui aussi pair, en contradiction avec la réduction à laquelle nous étions parvenus.Conclusion : puisque l"hypothèsep2 =
pq nous a conduit à une contradiction, c"est qu"elle est fausse, donc le Théorème est juste!!p2 1Néanmoins, bien que
p2soit un nombre irrationnel, il est très facilement accessible àla règle et au compas, puisque dès qu"on possède un carré de côté1, le compas peut être
"piqué» en deux sommets diagonalement opposés dans le carré, ce qui construitp2. Le traité géométrique desÉlémentsd"Euclide, de par sa puissance et sa nouveauté, a contribué pendant deux millénaires à engager la communauté mathématique dans la re- cherche de résolutions de problèmes de plus en plus difficiles, et ce avec une confiance très forte. En effet, puisquep2est constructible à la règle et au compas, et (voirplus bas) puisque toutes les racinespnsont elles aussi constructibles à la règle et au compas, pen-dant près de 2000 ans, les mathématiciens-géomètres ont été persuadés que la règle et le
compas permettraient d"atteindre toutes les longueurs visibles naturellement dans le plan. Les géométres Grecs considéraient que la droite et le cercle sont les deux seules figures fondamentales, parfaites, idéales, et ils ne validaient un problème de construction que s"il était réalisé à la règle et au compas.8 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Mais historiquement parlant,trois ou quatreproblèmes épineux ont indéfiniment résisté
à l"assaut des chercheurs, amateurs ou 'professionnels", sans jamais épargner leurs souf- frances. Les plus connus de ces problèmes très difficiles sont : la quadrature du cercle(le plus difficile de tous); la construction d"un polygone régulier à7côtés; la duplication du cube(le plus 'mélancolique" de tous); la trisection de l"angle.3.1.Bissection et trisection d"un angle quelconque.Il se trouve que les deux construc-
tions les plus simples et naturelles à la règle et au compas sont :lamédiatriced"un segmentAB(nous effectuons un rappel page 18 plus bas);
plus bas). Ensuite,puisqueaprèslechiffre2,toutlemondesait - mêmelesAustralopithèques - qu"il y a le chiffre3, il est naturel de se demander si l"on peut diviser un segment un trois parties égales? et aussi, si l"on peut diviser un angle en trois parties égales? Or diviser un segment donné en trois segments de longueurs égales est assez facile avec une règle et un compas (nous effectuons aussi un rappel de cette construction page 34 plus bas).Au contraire,diviser un angle en trois parties égales à la règle et au compas est un problème que les Grecs n"ont pas su résoudre.3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 9
Problème légué par les Grecs.Peut-on toujours, à la règle et au compas, diviser un angle
donné en trois parties égales? C"est un des premiers problèmes qui a fait très mal pendant très longtemps.3.2.Duplication du carré et duplication du cube.Ensuite, étant donné un carré de côté
de longueur1, donc d"aire11 = 1, il est facile de trouver un carré d"aire double : il suffit de tracer la diagonale, et de former (avec une règle et un compas) un nouveau carré sur cette diagonale4.4. Dans le dialogue socratiqueLe Ménonde Platon, Ménon est un aristocrate noble de Thessalie origi-
naire de Pharsale, mercenaire des Perses, élève sophiste, et ami du rhéteur sophiste Gorgias.
À la demande de Socrate qui veut illustrer saThéorie de la réminiscence, Ménon fait venir l"un de ses
esclaves.Socrate trace un carré dont il marque les transversales (en gras et pointillé) et il demande au jeune esclave
de trouver la marche à suivre pour construire un carré dont la surface serait le double de l"original (en gras).
Le côté du carré vaut2. Il a donc une surface de4, et il faut construire un carré dont l"aire vaut8.
L"esclave répond qu"il faut doubler la longueur des côtés. Cette réponse erronée (pourquoi?) constitue
alors un premier pas vers la réminiscence.Socrate demande en effet alors à Ménon d"observer l"esclave en train de se remémorer la suite, "car c"est
ainsi qu"on doit se remémorer».Puis pour containcre l"esclave de son erreur, Socrate trace le carré de côté double : il faut se rendre à
l"évidence, son aire n"est pas deux, mais quatre fois plus grande, elle vaut44 = 16, soit le double de8,
l"aire recherchée.L"esclave propose alors de construire un carré dont le côté vaut3. Mais un tel carré a une aire de9, ce
qui n"est pas non plus le résultat demandé.L"esclave est désormais dans l"embarras, ce qui rappelle une forme de torpeur que Ménon avait déjà
éprouvée face à Socrate, lequel y fait explicitement allusion en utilisant le terme deraie-torpille, un poisson
qui se défend en provoquant des électrochocs.Mais selon Socrate, l"esclave a, sans s"en rendre compte, déjà parcouru du chemin : "à présent le voilà
qui considère désormais qu"il est dans l"embarras, et tandis qu"il ne sait pas, au moins ne croit-il pas non plus
10 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Alors le nouveau carré sera effectivement d"aire double :
p2p2 = p22= 2 = 212:p2
1Mais qu"en est-il pour un cube?Étant donné un cube peut-on construire un cube ayant le double du volume? Sachant
que le volume d"un cube de côté de longueura >0vaut : a 3; il s"agit de construire un nouveau cube de côtéb >0tel que : b3= 2a3;
et en se ramenant àa= 1après normalisation, cela revient à construire un cube de côté de
longueur :b=3p2:qu"il sait». Il est maintenant dans une meilleure situation qu"avant, et Ménon en convient. En particulier, cela
est profitable parce quejamais on ne cherche ce que l"on croit savoir.Socrate trace les diagonales. Il apparaît que le carré construit sur la diagonale du carré initial est le carré
recherché. L"esclave le découvre et affirme maintenant que c"est sur cette ligne que l"on construit un carré
deux fois plus grand que le premier - ce qu"il ignorait complètement un instant auparavant.Conséquences générales sur la Théorie de la Réminiscence de Socrate.La connaissance mathématique
se tire de notre propre fonds - sinon l"esclave aurait soit reçu la connaissance à un moment donné, soit il
la possèderait depuis toujours. Pour posséder une connaissance, puisque la vérité est depuis toujours inscrite
dans l"âme (immortelle), ce que l"on se trouve ne pas savoir à un momement donné, c"est-à-dire ce dont on ne
sesouvientpas, c"est avec assurance et confiance que l"on doit s"efforcer de le chercher et de se le remémorer.
Socrate insiste sur les conséquences les meilleures selon lui : il faut oublier le scepticisme des sophistes pour
lui préférerl"ardeur et le zèle dans la recherche.3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 11
Problème légué par les Grecs.Peut-on toujours, à la règle et au compas, étant donné un
segment de longueur1, construire un segment de longueur : 3 p2? L"histoire raconte que l"oracle de l"île de Délos demanda que l"on double l"autel deforme cubique dédié à Apollon afin d"apaiser la colère des Dieux et de débarrasser l"île de
la peste. Les déliens (habitants de l"île de Délos) qui doublèrent alors la longueur des côtés
du cube ne résolurent pas le problème puisqu"ils multiplièrent ainsi le volume de l"autelpar huit. La peste redoubla d"intensité et les déliens, désemparés, allèrent trouver Platon
qui leur déclara qu"il est très préjudiciable aux grecs de négliger les mathématiques et la
géométrie.Dans la célèbre gravure d"Albrecht Dürer intitulée "Melancholia», l"ange est figure
etou de la mélancolie5. Une interprétation possible de cette gravure est la suivante. Dans un monde humainsous l"emprise des ténèbres, Dürer laisse entrevoir une aspiration vers un monde angélique
éloigné, l"homme espérant accéder à une lumière divine oubliée.5. Étymologiquement, mélancolie signifiebile noire humeur noire. Un tempérament mélancolique com-
porte parfois dépression, neurasthénie.12 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015La gravure comporte aussi un aspect allégorique
6, puisque leputto7et l"ange sont deux
figures allégoriques parallèles (par leurs ailes). Assis tous deux, tournés dans la même di-
rection, ils tiennent des objets semblables, et notamment, un compas. Perchée sur une roue de meunier, ou sur une meule à aiguiser, la figure duputtorappelle manifestement l"image- rie de laRota fortunamédiévale. Loin de se ressembler, les deux personnages s"opposent :le plus petit est occupé à griffonner, tandis que le plus grand semble avoir abandonné toute
velléité. Les outils sur le sol, près du grand ange, se rapportent au travail de la pierre, et peut-être sont ils destinés à évoquer la réduction en pierre cubique du grand polyèdre, problème
vraisemblablement difficile et source demélancolie. et au compas un hexagone régulier inscrit dans un cercle de centreO: en partant d"un point Psur le cercle, il suffit simplement de reporter6fois avec un compas, le rayondist(O;P).P OPO En choisissant un sommet sur deux, il est facile de déduire d"un hexagone régulier un triangle équilatéral inscrit dans le même cercle.P OIl est facile, aussi, de construire un carré inscrit dans un cercle.6. Dans l"Art littéraire, uneallégorieconsiste en une narration inventée, souvent accompagnée de des-
criptions métaphoriques dont les éléments sont cohérents, afin de représenter avec précision une idée générale
de la Pensée. "Le Roman de la Rose, longue allégorie de la conquête amoureuse».Dans les Arts plastiques, l"allégorie consiste en une représentation d"entités abstraites par des êtres ani-
més, auxquels sont associés des attributs symboliques. "L"allégorie du Printemps, par Sandro Botticelli».
7. Jeune garçon nu représentant l"Amour, dans la peinture italienne.
3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 13
Bien que cela soit moins élémentaires, il existe plusieurs constructions à la règle et au compas d"unpentagonerégulier -5côtés tous de même longueur - inscrit dans un cercle, lesquelles seront présentées ultérieurement.3,4,5,6côtés, on espère pouvoir faire de même pour un polygone à7côtés.C"est encore un problème que les Grecs n"ont pas su résoudre!
Problème légué par les Grecs.Peut-on toujours, à la règle et au compas, étant donné un
cercle de rayon1, construire un polygone régulier à7côtés? à9côtés? à11côtés? à13
côtés? etc.3.4.Quadrature du cercle.Partant d"un disque dans le plan, le problème demande de
construire un carré dont l"aire est égale à celle du disque.14 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015Le carré ayant pour côtéc >0et le cercle pour rayonr >0, le problème revient à
résoudre - à la règle et au compas! - l"équation : c2= r2:Grégoire de Saint-Vincent
8était tellement passionné par le problème qu"il écrivit un
ouvrage de 1000 pages, et il estimait (erronément!) l"avoir résolu. Ce problème est resté populaire et de nombreux quadrateurs amateurs envoient encore aujourd"hui de fausses preuves aux académies scientifiques. Métaphoriquement et encore de nos jours, "Chercher la quadrature du cercle»est une expression désignant un problème insurmontable. En tout cas, rappelons qu"il revient au même de savoir si l"on peut construire à la règle et au compas un segment de longueur égale, non à l"aire, mais à lacirconférence: 2 r; d"un cercle donné de rayonr >0. En effet, c"est dans le traité d"Archimède intituléLa Mesure du Cercleque l"on trouve les premières démonstrations connues et rigoureuses relatives à. Nous ne possédons d"ailleurs qu"une copie relativement tardive de ce traité et la pensée originale du savant syracusain nous est certainement parvenue déformée. Il semble que c"est Antiphon 9qui proposa le premier de quarrer le cercle en construisant des polygones ayant un nombre decôtés de plus en plus grand. Motivé par l"échec d"Anaxagore, Antiphon prétendait avoir
résolu par cela la quadrature du cercle. En effet, on sait construire un carré de même aire qu"un polygone régulier.=+OPour quarrer un polygone convexe arbitraire
(et en particulier un polygone régulier inscrit dans un cercle, comme Antiphon, il suffit de diviser le polygone en un nombre fini de triangles centrés un un pointO. Chaque triangle est suivante : bien sûr quarrable, car il est équivalent à un rectangle d"aire égale, comme le montre d"abord la figure triangle rectangle est équivalent à un rectangle d"aire égale. et le lecteur vérifiera par lui-même que tout Hélas, toute la difficulté est de savoir si l"on atteint vraiment le cercle en un nombre finid"étapes ou "à la limite", si les Grecs pouvaient donner un sens à ce terme auVesiècle.8. 1584-1667, jésuite, mathématicien et géomètre de l"école belge, connu pour le lien qu"il effectua
entre la fonction logarithme et les aires de sections d"hyperboles.9. Grand orateur Athénien du V
èmesiècle avant J.-C., sophiste hédoniste et aristocrate convaincu.3. Prologue sur les constructions à la règle et au compas et sur les problèmes impossibles 15
La chose n"est pas très claire à l"époque et Antiphon soutient que puisqu"on peut quar- rer individuellement chacun des polygones réguliers inscrits qui approximent le disque avec une précision arbitraire, alors on peut aussi quarrer le cercle. L"erreur qu"il commet constitue un obstacle épistémologique classique : la non-commutativité de certaines rela- tions logiques, ici par exemple, le fait que si pour toutn, le polygoneP3:2nà3:2ncôtés est quarrable, alors pourn=1, le cercleC=P1est lui aussi quarrable ; de même, l"interversion d"une limite et d"une intégrale,limn!1R 10fn(x)dx=R1
0(limn!1fn(x))dx
n"est pas toujours justifiée ; et pour prendre un exemple contemporain d"Antiphon, il n"est pas vrai quep2soit rationnel bien quep2puisse être approché par des nombres rationnels avec une précision arbitraire::: L"idée des constructions géométriques par approximations en nombre infini est née à cette époque, et c"est Eudoxe de Cnide (408-355 avant J.-C.) puis Archimède qui pous- sèrent le plus loin ce qu"on appelle leprincipe d"exhaustion: en prenant un nombre as- sez grand de figures géométriques rectilignes qui approximent par le haut et par le bas la longueur, l"aire ou le volume d"une figure géométrique courbe, on peut calculer rigoureu- sement leur longueur, leur aire et leur volume : on les arecouvertes exhaustivementpar des figures quarrables qui encadrent la figure courbe. Le calcul deest l"exemple le plus paradigmatique de la méthode d"exhaustion. Mais nous avons oublié jusqu"à présent de définir le nombre. Par définition,est égal au rapport de la circonférence d"un cercle sur son diamètre. Un cercle est l"ensemble des points qui sont équidistants d"un point fixé dans le plan. Maisest aussi le nombre égal au rapport de l"aire d"un disque sur le carré de son rayon. La définition de ce nombrecache en vérité trois théorèmes, tous démontrés rigoureusement par Archimède en utilisant
laméthode d"exhaustionsur laquelle nous allons revenir.Théorème 3.2.Le rapport du périmère d"un cercle sur son diamètre est une constante qui
ne dépend pas du diamètre du cercle.R2=aireR=rayon
D=diamètreD=périmètre
Théorème 3.3.Le rapport de l"aire d"un disque sur le carré de son rayon est une constante qui ne dépend pas du rayon du disque. Théorème 3.4.Ces deux constantes sont égales à un nombre que l"on note.16 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015R
2RThéorème : si le périmètre
Le disque de rayonR, découpé
à aire constante en un triangle rectangleselon l"un de ses rayons, se déroule de baseRet de hauteur2R.est2R, alors l"aire vautR2.Je laisse au lecteur le soin de démontrer par lui-même les trois théorème ci-dessus. Nous
allons maintenant voir comment l"on calculepar la méthode d"exhaustion.3.5.Extension et limites des constructions à la règle et au compas.Fill ??Ensuite, il va s"agir de conceptualiser la notion de construction géométrique avec les
et de se poser des questions concernant la puissance de ces moyens. En effet, les mathématiques plus récentes sont parvenues à comprendre quelle était l"ex- tension maximale des constructions à la règle et au compas. Commençons par présenter un catalogue de procédés de construction.4.Géométrie métrique dans le plan euclidienR2
Soit le plan euclidien réel :
P:=R2=(x;y):x2R; y2R;
contenant l"origine comme point central :O:= (0;0):
SoitP= (x;y)un point quelconque de ce plan. Ladistance euclidienne standardentreO etPest définie comme étant : dist(O;P) :=px2+y2:y
yP= (x;y)
x xpx 2+y2O= (0;0)
Lorsque leplanP=R2est vucommeespace vectoriel(espace devecteurs), ladistance entreOetPest égale à lanorme euclidienne(longueur) du vecteur allant du pointOau pointP: dist(O;P) =!OP:5. Symétrique d"un point par rapport à un point central 17
y xpx 2+y2 Et bien entendu aussi, la figure en coordonnées cartésiennes incorpore le : Théorème de Pythagore.Dans un triangle rectangle de côtésxety, le carré de la lon- gueur de l"hypothénuse et égal à la somme des carrés des deux côtés : px2+y22=x2+y2:
Plus généralement, étant donné deux points quelconques deP:A= (xA;yA)etB= (xB;yB);
ladistanceentreAetBest la quantité : dist(A;B) :=p(xBxA)2+ (yByA)2:y x xBOp(yAxA)2+ (yBxB)2
xAB= (xB;yB)
A= (xA;yA)yAy
BCest aussi lanorme euclidiennedu vecteur!AB.
À partir de maintenant, nous allons raisonner comme si tous nos objets vivaient dans le plan cartésien de coordonnées(x;y)dansR2, afin de nous assurer que toutes nos construc- tions sont bien fondées.5.Symétrique d"un point par rapport à un point central
Fixons un pointO2P. Il n"est pas nécessaire de penser que ce pointOest l"origine, puisque nous allons effectuer des constructions géométriques sans utiliser de coordonnées cartésiennes(x;y), en procédant comme le faisaient Euclide et ses contemporains.Soit à nouveauP2Pun point quelconque du plan.
Traçons le segmentOP.O
P OPTraçons le cercle de centreOpassant parP.
Traçons la droite(OP).
18 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Sud, 2014-2015O
P OP P 0 Alors cette droite(OP)intersecte le cercle en un unique autre pointP0, appelé lesymé- trique dePpar rapport àO. Proposition 5.1.Le symétriqueP0d"un pointPpar rapport à un pointOest constructibleà la règle et au compas.
Démonstration.En effet, on a utilisé la règle pour tracer un segment, puis le compas pour tracer un cercle, et enfin la règle pour prolonger le segment.quotesdbs_dbs11.pdfusesText_17[PDF] propriété cercle circonscrit triangle isocèle
[PDF] comment résoudre un carré magique
[PDF] groupe national mathématiques f boule fiches jeux
[PDF] carré magique ce2 ? imprimer
[PDF] carré magique pdf
[PDF] cours de conjoncture économique
[PDF] analyse de la conjoncture économique cours
[PDF] cours de conjoncture economique pdf
[PDF] cycle demi fond lycée
[PDF] situation ludique demi fond
[PDF] demi fond cycle 4
[PDF] carré magique avec nombres relatifs
[PDF] insee code ape
[PDF] insee pension alimentaire
