Corrigés 1 et 2 : Symétrie et groupes ponctuels
La molécule contient également un centre d'inversion et un axe S6. Exercice 1.3. Démontrez à l'aide d'un diagramme de coordonnées que S2 ≡ i et S1 ≡ σ. S2 se
TD n 1 – Opérations de symétrie et représentations dun groupe 1
On applique C3σyz puis σyzC3 `a la molécule : en numérotant les hydrog`enes on ne trouve pas la même structure. 4. `A quels groupes ponctuels de symétrie
Présentation PowerPoint
exercice: rep. Question: Quel est l'effet sur l'énergie d'une molécule si on lui applique une opération de symétrie (appartenant à son groupe ponctuel) ?
Sans titre
Le groupe ponctuel résultant est le groupe 4/mmm. Groupe ponctuel d'un cube. Énumérer les éléments de symétrie d'un cube selon des principales directions.
Symétrie
Déterminer le groupe ponctuel de la molécule suivante. Indice : Il y a cinq classes. 3.4 Produit de représentation. Déterminer le résultat des produits
Exercices 1 et 2 : Symétrie et groupes ponctuels
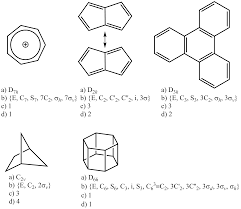
Exercices 1 et 2 : Symétrie et groupes ponctuels. Exercice 1.1. Pour les molecules suivantes identifiez a) les axes de rotation propres b) les plans de
Dans les réponses numérotez chaque réponse clairement. Il sera
Il sera tenu compte de la clarté de la copie dans la note finale. Exercice 1 (5 points) b) Déterminer le groupe ponctuel de symétrie de la molécule. c) ...
Table des matières
Spectroscopie cours et exercices
MP059 : Symétries en Physique
1 avr. 2011 doit être invariant par les opérations du groupe ponctuel de symétrie (donc un sous-groupe ... Exercice : groupe de Lorentz. C'est l'ensemble des ...
Symétries et Groupes
23 oct. 2010 axes hélicoïdaux miroirs à glissement …. → 32 groupes ponctuels (classes de symétrie des systèmes cristallins). → 230 groupes d'espace des ...
Corrigés 1 et 2 : Symétrie et groupes ponctuels
Corrigés 1 et 2 : Symétrie et groupes ponctuels. Exercice 1.1. Pour les molecules suivantes identifiez a) les axes de rotation propres.
TD n 1 – Opérations de symétrie et représentations dun groupe 1
On applique C3?yz puis ?yzC3 `a la molécule : en numérotant les hydrog`enes on ne trouve pas la même structure. 4. `A quels groupes ponctuels de symétrie
Sans titre
En utilisant une représentation analogue à celle de l'exercice précédent représenter le groupe ponctuel 422. Quelle est la multiplicité d'un point en
Chapitre 2: Les groupes ponctuels
Pour déterminer le groupe ponctuel d'une molécule plus facilement il suffit de déterminer quelques éléments de symétrie caractéristiques à l'aide d'un
Dans les réponses numérotez chaque réponse clairement. Il sera
Seuls les documents « Détermination du groupe de symétrie » Exercice 1 (5 points) ... b) Déterminer le groupe ponctuel de symétrie de la molécule.
Licence de Chimie 2017-2018 Symétries : Travaux Dirigés
Chaque TD se découpe en une série d'exercices visant `a vous familiariser Déterminer la représentation matricielle du groupe ponctuel de symétrie de NH3 ...
Symétrie
Déterminer le groupe ponctuel de la molécule suivante. Indice : Il y a cinq classes. 1. si l'état initial d'une molécule de symétrie C2v est A1.
MP059 : Symétries en Physique
Cn une rotation de ? autour d'un axe orthogonal `a u; et les trois groupes de symétrie de rotation des solides platoniciens (voir § suivant et exercice en
LP 339 Année 2013 – 2014 TD n°3 : SYMETRIES – GROUPES
(directions équivalentes par symétrie). • En utilisant une représentation analogue à celle de l'exercice précédent représenter le groupe ponctuel 422.
Untitled
Eléments opérations et groupes ponctuels de symétrie. A partir des données regroupées en annexes
TD n 1 – Op´erations de sym´etrie et repr´esentations d’un groupe
Pour v´eri?er qu’on a bien fait la liste de toutes les op´erations de sym´etrie on est oblig´e de d´eterminer `a quel groupe ponctuel de sym´etrie appartient la mol´ecule et on regarde sa table de caract`eres : sur la premi`ere ligne on trouve les classes d’op´erations de sym´etrie 2
Groupes ponctuels de symétrie - scienceamusantenet
Corrigés 1 et 2 : Symétrie et groupes ponctuels Exercice 1 1 Pour les molecules suivantes identi?ez a)les axes de rotation propres b)les plans de ré?exion c)les centres d’inversion d)les axes de rotation impropres Tableau de résumé : Molécule Axes de rotation propres Plans de ré-?exion Centre d’inversion Axes de rotation
Exercices 1 et 2 : Symétrie et groupes ponctuels - EPFL
Exercices 1 et 2 : Symétrie et groupes ponctuels Exercice 1 1 Pour les molecules suivantes identi?ez a) les axes de rotation propres b) les plans de ré?exion c) les centres d’inversion d) les axes de rotation impropres Exercice 1 2 Déterminez les éléments de symétrie du cyclohexane (conformations chaise et bateau) Exercice 1 3
Master 1 – Chimie 137UD03 – Symétrie moléculaire et
1 positionnez les éléments de symétrie présents (sur chaque figure ci-dessous) 2 listez les éléments de symétrie 3 proposez un groupe ponctuel de symétrie 4 dire si la molécule ou l'objet est polaire Benzene biphenyl chromium Dibenzènechromium Ni(cyclobutadiène) 2 éclipsé Eléments de symétrie Groupe ponctuel polarité
Searches related to exercices groupe ponctuel de symétrie PDF
Groupe ponctuel d’une molécule Le complexe MX4 a la forme d'un tétraèdre régulier dont le centre est occupé par l'atome M et les sommets par les atomes X • Énumérer les éléments de symétrie que possède la molécule En déduire son groupe ponctuel puis déterminer son système cristallin
Quels sont les groupes ponctuels de symétrie ?
Voici les tables de caractères des principaux groupes ponctuels de symétrie. Dans les tables, ? désigne un nombre complexe précisé dans le tableau, et ?* désigne son conjugué complexe.
Quel est le groupe ponctuel de symétrie de l'unité asymétrique?
Le groupe ponctuel de symétrie de l'unité asymétrique est 1 lorsque l'on considère les atomes qu'elle contient : il ne contient pas d'autres opérations de symétrie que l' identité, d'où le nom « asymétrique ». Cependant, la forme du volume défini par l'unité asymétrique peut avoir une symétrie supérieure.
Qu'est-ce que la grande symétrie?
La grande symétrie implique la symétrie de C . Au ?nal, on identi?e facilement que le nombres de composantes indépendantes de C (ou de ) est de 21. Les mathématiciens nomment l’espace des tenseurs d’élasticité (du 4e ordre, munis des petites et grandes symétries).
Quels sont les groupes de symétrie?
6 groupes tétartoèdres (non centrosymétriques) ayant le quart du degré de symétrie du réseau 3, 4, ?, 6, ?et 23 19 groupes hémièdres ayant la moitié du degré de symétrie du réseau ponctuel 25 groupes mérièdres Classification des 32 groupes de symétrie 26
MasterdeSciences etTec hnologies
MentionPhysiqueet Applications
MP059:Sym ´etr iesenPhysique
Jean-BernardZuber
Versiondu1
er avril2011 Figure1-Pierre Curie(1859-1906)qui donne`a notreUniv ersit´e (lamoiti ´ede) sonnom,estungrandph ysicien.Ilest enparticulier`al"originede nombreusesid ´ees surlerˆ oledessym ´etries
enPhysique, commeonverradans cespages. ..Tabledesmati`er es
1Sym´ etriesg´eom´etriques.Desmol´ecules auxcristaux3
1.1G´ en´eralit´essurlessym´etries.......... ... ... ........ ... ..3
1.1.1Transformations del"espaceetsym´ etries.. ... ... ........ ..3
1.1.2Unp etitalbumd"images. ...... ... ........ ... ... ... .4
1.1.3Isom ´etriesetd´eplacements..... ... ........... ... ... .8
1.2R´ eflexion-miroiretinversion/parit´e. ... .............. ... ... .9
1.2.1Isom ´etriesimpropres......... .. ... ... ... ... ... ... 9
1.2.2R´ eflexion-miroir........ ... .. ... ... ... ... ... ... .9
1.3Rotationset r´ eflexionsdeR
2 etdeR 3 ... ... .. ... ... ... ... ... .111.3.1Groupes O(d)etSO( d).. ... .. ... ... ... ... ... ... ... 11
1.3.2Sous-groupes finisdesgroupesderotation `ad=2et d=3. ... .. ..11
1.3.3Groupes d"invariancedespolygones etdespoly`edres.. ... ...... 11
1.3.4Groupes ponctuels... ...... ... ... ... ... .. ... ... .13
1.4Sym´ etriesdesmol´ecules.... ... ........ ... ... ... ... ... .14
1.5Sym´ etriesd"uncristal...... ... .. ... ... ... ... ... ... ... .15
1.5.1R´ eseauxdeBravais.... ... ........ ... ... ... ... ... 16
1.5.2Cristallographie` adeux dimensions..... ... ... ... ... .. ..17
1.5.3Cristallographie` atroisdimensions ...... .. ... ... ... ... .21
1.5.4Autresordres translationnelsou orientationnels. ... ... ..... ..28
1.6Exercices. .. ... ... ... ... ... ... ... ... .. ... ... ... ..28
2Tr ansformationsdesgrandeursphysiques31
2.1Rotations. .. ... ... ... ... ... ... ... ... .. ... ... ... .31
2.1.1Vecteurs etscalaires... ... ... ... ... ... .. ... ... ... 31
2.1.2Tenseurs. Exemplesphysiques... ... ..... ... ... ... ... .34
2.2R´ eflexionsetInversion/Parit´e. ... ................. ... ... .36
2.2.1Scalaireset pseudoscalaires,vecteurs etpseudov ecteurs. ...... ... 36
2.2.2Cov ariancedesgrandeursetinvariancedeslois delaph ysique. ... ..37
2.3Principe deCurie.... ... ... .. ... ... ... ... ... ... ... .. 38
2.3.1Applicationsph ysiquesd"arguments desym´etrie.. ..... ... ....38
2.3.2Principe deCurie.... ... ... .. ... ... ... ... ... ... .39
2.3.3Autresillustrations duprincip edeCurie ... ...... ... .. ... .40
2.4Translations ...... ... ... .. ... ... ... ... ... ... ... ..41
2.4.1Di
ff ractioncristalline, loidev onLaue. ... ...... ... .. ... ..412.4.2Zonesde Brillouin.. ... ... .. ... ... ... ... ... ... ..42
2.5Modes propresdevibrationd"unemol´ ecule.. ... .. ... ......... ..43
2.6Exercice. ... ... ... ... .. ... ... ... ... ... ... ... ... .44
TABLEDESMATI
ERES3Brisure spontan´ee desym´etrie45
3.1Brisuresp ontan´ eedesym´etriediscr`ete...... ... ......... .....45
3.1.1Unmo d` elem´ecanique........ ......... .. ... ... ... 45
3.1.2Ferromagn ´etisme.......... .. ... ... ... ... ... ... .46
3.1.3Mod `eled"Ising........ ... ... ... ... .. ... ... ... .47
3.1.4Unparado xe?. ......... .. ... ... ... ... ... ... ... 49
3.2Brisuresp ontan ´eedesym´etriecontinue...... ... ........ ......49
3.3Autresexemples desym´ etriesbris´ eesspon tan´ement.... ......... ...50
3.4Exercice: Champmoy en.. ... ........ ... ... ... ... ... ..52
4Groupes continus.G´ en´erateursinfinit´esimaux.Lois deconservation55
4.1Transformations continues,g´ en´erateursinfinit´esimaux... ............55
4.1.1Groupes destranslationsR,R
d .......................554.1.2Groupe desphasesU(1)... ... ... .. ... ... ... ... ... .56
4.1.3Groupe derotation`adeuxdimensions SO(2).. ... ..... ... ... 57
4.1.4Groupe derotation`atrois dimensionsSO(3). ... ...... ... .. .58
4.1.5Groupe deLie,alg`ebrede Lie,etleur dimension.. ........ ... .58
4.2Sym´ etriescontinuesetloisdeconserv ation........ ... ... .. .....61
4.2.1Formalisme lagrangienetformalismehamiltonien. ... .. ...... .61
4.2.2In variancesetloisdeconservation..... ... .. ... ...... ... 62
4.3Inv ariancedejaugedel"´electrodynamique. ... .. ... ............ 65
4.4Exercices. ... ... ... ... .. ... ... ... ... ... ... ... ... .66
5Repr´ esentationsdesgroupes69
5.1D´ efinitionetpropri´et´esg ´en´ eralesdesrepr´esentations........ .......69
5.1.1D´ efinitionsdebase...... ... .. ... ... ... ... ... ... .69
5.1.2Repr´ esentations´equivalentes.Caract`eres.. ............ ....70
5.1.3Repr´ esentationsr´eductiblesetirr´eductibles.. ......... .. ....72
5.1.4Repr´ esentationsunitaires........ ... ... ... .. ... ... ..73
5.1.5Lemmede Schur ... ......... .. ... ... ... ... ... ..75
5.2Repr´ esentationsdesgroupesfinis..... ... ...... .. ... ... ... .75
5.2.1Orthogonalit´ eetcompl´etudedesrepr´esen tations.. ........ ... .75
5.2.2Cons´ equences....... ... ... ... ... ... .. ... ... ... 78
5.2.3Ungroup econtin u:U(1).. ... ... ... ... ... .. ... ... .79
5.3Produits directsdegroupesoude repr´esen tations;d ´ecompositiondeClebsc h-
Gordan.. ... ... ... ... ... .. ... ... ... ... ... ... ... .805.3.1Produits directsdegroupesetleurs repr´esen tations.. ..... ... ..81
5.3.2Produit tensorielderepr´esentations ... .. ............ ... .81
5.4D´ ecompositiondesrepr´esentationsd"ungroupesurcelles d"unsous-group e...82
5.5Applicationsph ysiques.. ...... .. ... ... ... ... ... ... ... .83
5.5.1Modes devibrationdesmol´ ecules.. ... ... ........ ... ... 83
5.5.2Vibrationdes cristaux. ... ... ... ... ... ... ... .. ... .84
5.6Exercices. .. ... ... ... ... ... ... ... ... .. ... ... ... ..85
6Sym´ etriesenM´ecaniqueQuantique87
6.1Th´ eor`emedeWigner.......... .. ... ... ... ... ... ... ... 87
6.1.1Th´ eor`emedeWigner........... .. ... ... ... ... ... ..87
6.1.2In varianced"unsyst`emequantique... ... ......... ..... .88
6.2Sym´ etriesdiscr`etesenphysiquequan tique:parit´e,renversement dutemps,. ...90
TABLEDESMATI
ERES6.2.1Transformation d"un´etatquantique sousl"e
ff etdela parit´ e.. ......906.2.2Brisurede lasym ´etriede parit´e enphysiquedesparticules.... ... .92
6.2.3Renv ersementdutemps........ ... .. ... ... ... ... ..93
6.2.4Brisurede lasym´ etriederen versement dutempsenphysiquedesparticules94
6.3Sym´ etriesdetranslation,th´eor`emede Bloch .. ............... ... 94
6.4Application` alaph ysiquemol´eculaire.. ... ..... ......... ... ..95
6.5Sym´ etriesdelaphysiquedesparticules. ... ... ...... ... .. ... ..97
7Rotations` atroisdimensions. LegroupeSO(3)99
7.1Rotationsde R
3 ,legroup eSO(3),ses g´en´erateursinfinit ´esimaux. .. ......997.1.1Legroup eSO(3),group e`atroisparam` etres.. ..... ...... ... 99
7.1.2G´ en´erateursinfinit´esimauxdeSO(3)....... ........ ... ..100
7.1.3Alg` ebredeLieso(3).. ... ... ... ... ... .. ... ... ... .102
7.2Repr´ esentationsdeso(3)etdeSO(3).... ... ... ... .. ... ... ... 103
7.2.1Repr´ esentationsdel"alg`ebreso(3)..... .. ......... ... ... 103
7.2.2Repr´ esentationdespinjdugroupe SO(3)..... ... ... .. ... .105
7.3Coordonn ´eessph´eriques.Harmoniquessph´eriques... ........ ... ....108
7.4Produit tensorielderepr´esentations ... ... ........... ... ... ..111
7.4.1Produit directderepr´esen tationsetl""addition demoments angulaires".111
7.4.2Coe
ffi cientsdeClebsch-Gordan,sym boles3- j...............1127.4.3Th´ eor`emedeWigner-Eckart....... ... ........ ... ... .114
7.5Quelquesapplications physiques. ... ..... ... ... ... ... ... ... 115
7.5.1Moments multipolaires... ........ ... ... ... ... ... ..115
7.5.2Etatspropres demoment angulaireenM ´ecaniqueQuan tique.... ... 116
7.5.3L"isospin. ... ... ... ... .. ... ... ... ... ... ... ... 116
7.62Probl `emes. ......... ... .. ... ... ... ... ... ... ... .. 118
7.6.1Mol´ eculedefuller`ene.... ... ........ ... ... ... ... ..118
7.6.2Champcristallin .. ... ... ... ... ... ... ... .. ... ... 121
Bibliographie
[1]C.Aslangul,Cours demagist `ereENS-P6, Physiquedela Mati`er eCondens´ ee [2]C.Aslangul,M´ecaniqueQuantique,tome2, deBroec k,2009 [3]J.-P.BlaizotetJ.-C.T ol´edano, Sym´etriesetphysiquemicroscopique,Ellipses [4] E.Br´ ezin,R.MosserietJ.-C.Toledano, Sym´etries,sym´etriesbris´ees ,Cours` al" EcolePolytechnique
[5]J.Hladik,Lath´eoriedes groupesenphysiqueetchimiequantiques ,Masson1995. [6]C.Kittel,IntroductiontoSolidStatePhysics,JohnWiley &Sons (7thedition1995) [7]L.Landauet E.Lifshitz,Th´eoriedel"´elasticit´e ,´editions Mir. [8]L.Landauet E.Lifshitz, Electrodynamiquedesmilieuxcontinus,´editions Mir. [9]L.Landauet E.Lifshitz, M´ecaniquequantique,´editions Mir. [10]L.Landauet E.Lifshitz,M´ecaniquestatistique,´editions Mir. [12]M.Tinkham,GroupTheoryandQuantum Mechanics,McGraw-Hill [13]J.Sivardi `ere,Descriptiondela sym´ etrie,EDP [14]L.Valen tin,Physiquesubatomique :noyauxetparticules ,Hermann [15]S.Wein berg,TheQuantumThe oryofFields ,Cambridge Univ.Press Parmicesouvrages,certainsson t´ecrits dansunesprit assezproc hedeceluidupr ´esentcours, enparticulier,[3, 4,5]. Ontrouvera beaucoupde d´etails suppl´emen tairesdans[9,10,12,14] etdenom breuxexempleset applicationsdanslesautres. 12BIBLIOGRAPHIE
Chapitre1
Sym´etriesg´eom´etriques.Desmol ´ecules auxcristaux1.1G´ en´eralit´essurlessym´etries
1.1.1Transfor mationsdel"espaceetsym´etries
Toutaulongdece coursonv as"int ´eresser` adestransformationsdel"espace. Par"espace",onentend l"espaceph ysique,espaceeuclidien `addimensions,av ecd=3dans la situationlaplus courante,mais d=1et d=2p ouvant aussijouerunrˆole(chaˆınespolym ´eriques unidimensionnelles,substratset autrescompos ´esbidimensionnels, etc).P arlasuite,cecontexte sera´elargi `ad"autressituations,telled=4a vecl"espace-temps deMinkovski(quin"estplus euclidien),ou` adesespaces plusabstraits,espacesdesym´ etrieinterne d"isospinou dejauge, etc. Par"transformation",onentend unetransformationp onctuelleinv ersible,quiassocie` achaque pointdel"espaceconsid´er´ eunp ointet unseuldumˆemeespace,ettellequ"`apartirdetout pointimage,onpuisserevenirde fa¸conunique aupoin td"origine :cetteconditiond"inversibilit ´e exclutparexemple destransformations commelapro jectionsur unsous-espace. D"unpoin tdevuemath´ematique,cestransformationsformen tungroupe.Onp eutene ffetles composer:selonlacon vention usuelle,la compositiondes transformationst 1 puist 2 e ff ectu´ees danscetordre estnot´ eet 2 ◦t 1 ,out 2 .t 1 ousimplement t 2 t 1 .Elleasso cie` atoutpointxdel"espace lepoin ttransform´ex?→x =t 2 .t 1 (x)=t 2 (t 1 (x)).Cetteop ´erationde compositionestbien associative(c"est-`a-diret 3 .(t 2 .t 1 )=(t 3 .t 2 ).t 1 ,pourquoi ?),elleaun´el´ement neutre(l"op´ eration trivialex?→x)ettoute transformationadmetun inverse (notrehyp oth` esed"inv ersibilit´e). Parailleurs,nousallonsnous int´ eresser`a dessym´etries,c"est-`a-dire destransformations agissantsurunobjet g´eom ´etriqueou unsyst`emeph ysiqueetenpr´eservantdespropri´et´es g´eom´etriques(parexemplelesdimensions,oulesangles,oulev olume...), oudes propri´et ´es physiques,structureinterne, dynamiqueetc.On distingueradoncleconceptdesym ´etriede celuidetransformation. Unetransformationagit surunsyst `emeph ysique,ses coordonn´ eesetsesautresdegr ´esde libert´e,maisn"estpasn´ ecessairementune sym´etrietellequ"onvientdela
d´efinir.Pournoustoutesym´ etrieestdoncli´ee `aune certaineinvariancedel"objet consid´er´e.
Toutcommelestransformations,les sym´etries d"unobjet g´ eom´etrique oud"unsyst`eme physiqueformentungroup e:lacompositionde deuxsym´ etriesestencoreunesym ´etrieetc. Onparledonc dugroupe desym´ etrie(oud"in variance)del"objet consid´er ´e. 34CHAPITRE1.SYM
ETRIESG
EOMETRIQUES.DESMOL
ECULESAUX CRISTAUX
Figure1.1-Les premierspolygones r´eguliers convexes ounon-convexes. Figure1.2-Les cinqpoly `edresr ´eguliersou "solidesplatoniciens":t´etra`edre,cube,o cta`edre, dod´eca`edreeticosa`edre(cfhttp://fr.wikipedia.org/wiki/SolidedePlatonpour plusded´etails).1.1.2Unp etitalbumd"images. ..
L"observationdesym´etries estcommune danslaviecourantecommedansle mondemath´ ema- tiqueouph ysique. Ellessemanifesten ten g´eom´etrie,bien sˆur ;enphysique,depuislam´ecanique(loisdeKepler, toupie,.. .),`alamin´eralogieetla cristallographieetauxsym´etries pluscac h´eesdumonde atomiqueousubatomique ;en botaniqueetenzoologie ;etdans lesconstructionshumaines, architecturales,artistiquesoutec hnologiques...Quelquespremiersexemples.
Eng´ eom´etrie,polygonesr´eguliers,encommen¸cantpar letriangle´equilat´eral, Fig.1.1;
poly`edresr´eguliers,quiensontl"analogue `a3dimensions.Lespoly` edresr´ egulierssont des solidesconv exesdonttouteslesarˆetes ontmˆemelongueur ettousles sommetset touteslesfacessont demˆemenature.Ils ont´ et´eclassifi´esparl" ´ecolede Platon,d"o` ulenomdesolides
platoniciens.Ceson tlescinq solidesdelafigure1.2,le t´etra `edre,le cube etl"octa `edre,et le dod´eca`edreetl"icosa`edre.Lesquatrederniersformentdespaires duales:les milieuxdesfaces ducube sontlessommetsd"uno cta`edrer´egulier etvicev ersa,et demˆ emepourledod´eca`edre etl"icosa` edre.Lefaitque laliste despoly `edresr ´egulierss"arr ˆetel` aestunecons´equencesimpledelacaract ´eristiqued"Euler:
lesnombres V,AetFdesommets,d"ar ˆetes etdefacessatisfontV-A+F=2p ourtoutp oly`edre,r´egulier oupas.Mais dansun poly` edrer´ egulier,si vestlav alence(nom bredevoisins)dec haquesommetetv celle desfaces(nom bredefaces adjacentes`achaque face),ona 2A=vV=vF.Doncen reportant danslarelation
d"Euler,( 2 v -1+ 2 v )A=2,et onsecon vaincrapidem entque lesseulesv aleurspossiblesde(v,v )sont (3,3)t´etra`edre;(3,4)cubeou(4,3)octa`edre;(3,5) dod´ eca`edreet(5,3)icosa `edre.T outev aleursup´erieuredevouv
conduit`a unmembredegauc hedela relationnuloun´ egatif. Danslemonde cristallin,detr `esb ellesstructures observ´ eesrefl`etentunesym´etrie micro- scopiquesous-jacente. -Ainsila glacepr´ esenteune grandevari ´et´edecristauxdesym´etriehexagonale, Fig.1.3; -lequartz, quichimiquemen test delasilice SiO 2 ,cristalliseen detr `esb eauxcristaux avecunesym´etried"ordre6, Fig.1.4,(mais enfaitdenombreusesautresformescristallines du quartzexistent danslanature,selonlatemp ´eratureou lapressionde formation); -ontrouv ebeaucoup d"autresexemples,telcecristald"alun dechrome,unocta `edre parfait detailleimp osante(162 mmdediagonale),Fig.1.4; -legraph `ene,un mat´eriaunouvellementd´ecouv ert,form´ ed"uncristaldecarbonebidimen- 1.1.G ENERALIT
ESSURLES SYM
ETRIES5
Figure1.3-Cristaux deglace.Quelles sontleurs sym´etries ?Source... Figure1.4-Cristaux dequartz,a vecau centre,le sch´ emad"uncristalid´eal,av ecsesaxes de sym´etrie.Adroite,cristal d"alundec hrome,Sourceshttp://pagesp erso-orange.fr/daniel.robert9/Digit/Digit6TS2.html;
Sourcehttp://www.dacg.nl/fot ogalerij.html,[R.Wagenaar,Europh ysicsnews40/12009p05] sionnel(d"une´ epaisseurd"un seulatome),quiexhibeune remarquablestructurehexagonale "ennidd"ab eilles"etdes propri´et´esph ysiques-transport ´electronique enparticulier-tout`a faitinattendues,Fig. 1.5. Enphysique mol´eculaire,desmol´ eculessimples(ammoniacNH 3 ,pyramide `abase´equilat´ erale, eauH 2 O,quellessym ´etries?), voirFig1.18,oupluscomplexestellelefuller` ene,Fig.1.6. Enbotanique etenzoologie,laNature semblen" ˆetrejamais `acourtd"id´ eesdesym ´etries originales,cfFig. 1.7. Lesmammif` eresonteng´en´eral unesym´etrieder ´eflexion d"ordre2,aumoinsglobalement, (Fig.1.8),sur laquellenous reviendronspluslonguemen tau§1.2. Enmati` erearchitecturaleetartistique,lesexemplesabonden taussi:Fig.1.9, Fig.1.10, maisaussidans ledomainedes objetsman ufactur´es parl"homme; ainsiles ailesdesmoulins`a ventetautres´eoliennes,lesh ´elicesou turbinestellescelles delaFig.1.11se doivent d"avoiruneFigure1.5-Graph `eneSourceWikipedia
6CHAPITRE1.SYM
ETRIESG
EOMETRIQUES.DESMOL
ECULESAUX CRISTAUX
Figure1.6-Mol ´eculeC
60defuller` ene,obtenue`apartird"unicosa` edreentronquant(traits rouges)descalottes autourde chacundes 12sommetset enpla¸can taux60nouveauxnoeuds desatomesde carbone. Figure1.7-caram bole,sanguinaire duCanada,rudbeckie,marguerite;´etoiles demer,
oursin,ruche d"abeilles,Sourcesshortcourses.com, http://britton.disted.camosun.bc.ca/fibslide/jbfibslide.htm,htt p://antimon-
santo.a.n.pic.centerblog.net/4y ff7p39.jpg
Figure1.8-Le squelettehumain pr´esen teunesym ´etrieparr´ eflexiondansunplan,cequin"est´evidemmen tpaslecasdelamain,saufquand elleestst ylis´ ee.. .Sourcehttp://www.p endentifs-
Figure1.9-P alaisdeV ersailles.TourEiffel.Dˆome del"´eglisede Mostar,Malte.Sources 1.1.G ENERALIT
ESSURLES SYM
ETRIES7
Figure1.10-"grecques", mosa¨ıque d"Aquilea(Italie),azulejo del"Alcazar,S´eville;gravure d"EscherSourcehttp://mcesc her.frloup.com/affichediapo.php?cat=6 sym´etrieparrotation(discr`ete)autour deleuraxe aussiparfaiteque possiblepour´eviterdu "ballant"causedevibrationset d"usure,maispar contrene sont passym´ etriquesparr ´eflexion, fautedequoi ellesnetourneraien tpas!quotesdbs_dbs44.pdfusesText_44[PDF] groupe d'espace pnma
[PDF] symétrie cristalline exercice corrigé
[PDF] les 230 groupes d'espace pdf
[PDF] exercices corrigés théorie des groupes chimie
[PDF] groupe d espace p21 n
[PDF] groupe d espace p212121
[PDF] nouvelles naturalistes des soirées de médan résumé
[PDF] les soirées de médan résumé détaillé
[PDF] les soirees de medan resume chapitre par chapitre
[PDF] les nouvelles naturalistes des soirées de médan
[PDF] les soirées de médan analyse
[PDF] commentaire composé germinie lacerteux
[PDF] rmn du proton exercices corrigés
[PDF] singulet doublet triplet quadruplet quintuplet sextuplet septuplet
