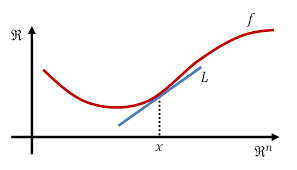
 Lecture 6: Subgradient Method September 13 6.1 Intro to
Lecture 6: Subgradient Method September 13 6.1 Intro to
Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These notes The subdifferential of the indicator function at x is known as the normal ...
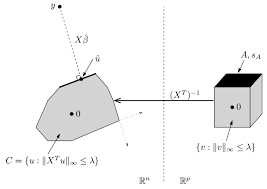 Lecture 13: February 25 13.1 Dual Norm 13.2 Conjugate Function
Lecture 13: February 25 13.1 Dual Norm 13.2 Conjugate Function
Note: LaTeX template courtesy of UC Berkeley EECS dept. conjugate of an indicator function is a support function and the indicator function of a convex set ...
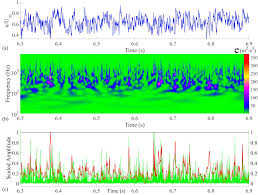 A wavelet-based detector function for characterizing intermittent
A wavelet-based detector function for characterizing intermittent
30 дек. 2022 г. 1s in the indicator function. The resulting value of γ(= 0.48) is ... Springer Nature 2021 LATEX template. Farge M. 1992. Wavelet transforms ...
 Indicator Power Spectra: Surgical Excision of Non-linearities and
Indicator Power Spectra: Surgical Excision of Non-linearities and
3 нояб. 2021 г. Compiled using MNRAS LATEX ... Comparison of the top and bottom panels demonstrates the superiority of indicator function methods over Monte Carlo ...
 Lecture 10: March 1 10.1 Conditional Expectation
Lecture 10: March 1 10.1 Conditional Expectation
Note: LaTeX template courtesy of UC Berkeley EECS dept. By generalizing X from an indicator function to any random variable we can get the definition of the.
 Robusta: Robust AutoML for Feature Selection via Reinforcement
Robusta: Robust AutoML for Feature Selection via Reinforcement
15 янв. 2021 г. We use 1{event} to represent an indicator function which is 1 if the event happens and 0 otherwise. We define s0 as the initial state. We ...
 Lecture 15: Log Barrier Method 15.1 Introduction
Lecture 15: Log Barrier Method 15.1 Introduction
Note: LaTeX template courtesy of UC Berkeley EECS dept. Figure 15.1: As t approaches ∞ the approximation becomes closer to the indicator function.
 Probabilities and random variables
Probabilities and random variables
Monthly; I was seeing how closely LATEX could reproduce the original text. E in the final indicator function; for those cases the indicator function is zero.
 Analysis and improvement of direct sampling method in the mono
Analysis and improvement of direct sampling method in the mono
7 окт. 2022 г. indicator function of DSM based on the asymptotic formula of the ... JOURNAL OF LATEX CLASS FILES VOL. 13
 Lecture 6: Subgradient Method September 13 6.1 Intro to
Lecture 6: Subgradient Method September 13 6.1 Intro to
Note: LaTeX template courtesy of UC Berkeley EECS dept. The subdifferential of the indicator function at x is known as the normal cone NC(x)
 Math 230.01 Fall 2012: HW 5 Solutions
Math 230.01 Fall 2012: HW 5 Solutions
Alternatively one can solve this with the method of indicator functions: let The expected value of an indicator function is the probability of the set ...
 Lecture 10: March 1 10.1 Conditional Expectation
Lecture 10: March 1 10.1 Conditional Expectation
Note: LaTeX template courtesy of UC Berkeley EECS dept. By generalizing X from an indicator function to any random variable we can get the definition of ...
 Machine Learning Notation
Machine Learning Notation
1(x; cond) The indicator function of x: 1 if the condition is true 0 otherwise g[f; x] A functional that maps f to f(x). Sometimes we use a function f
 Lecture 13: February 25 13.1 Dual Norm 13.2 Conjugate Function
Lecture 13: February 25 13.1 Dual Norm 13.2 Conjugate Function
This lecture's notes illustrate some uses of various LATEX macros. conjugate of an indicator function is a support function and the indicator function ...
 Probabilities and random variables
Probabilities and random variables
The indicator function of an event A is the random variable defined Monthly; I was seeing how closely LATEX could reproduce the original text.
 Problem Set 1
Problem Set 1
Turn in your problem sets electronically (LATEX pdf or text file) by email. (b) The indicator function 1{a} : {1
 arXiv:2108.01673v2 [astro-ph.CO] 3 Nov 2021
arXiv:2108.01673v2 [astro-ph.CO] 3 Nov 2021
Nov 3 2021 Compiled using MNRAS LATEX style file v3.0 ... We here introduce indicator functions
 The Hypervolume Indicator: Problems and Algorithms
The Hypervolume Indicator: Problems and Algorithms
May 1 2020 and
 LEBESGUE MEASURE AND L2 SPACE. Contents 1. Measure
LEBESGUE MEASURE AND L2 SPACE. Contents 1. Measure
KE is called the characteristic function or indicator function of E. Any simple function can be written as a finite linear combination of characteristic.
36-752 Advanced Probability Overview Spring 2018
Lecture 10: March 1
Lecturer: Alessandro Rinaldo Scribes: Wanshan LiNote:LaTeX template courtesy of UC Berkeley EECS dept.
Disclaimer:These notes have not been subjected to the usual scrutiny reserved for formal publications.
They may be distributed outside this class only with the permission of the Instructor.10.1 Conditional Expectation
Given a probability space (
;F;P), letC Fbe a sub--eld ofF, and a xed setA2 F. Our goal is to dene the conditional probabilityP(AjC). The point is that,Cprovides us additional information, soP(AjC) would be dierent fromP(A).
First we consider of a special caseC=(B1;;Bn) wherefB1;;Bngis a partition of . The additional information here is that, for any!2 , one knows whether!2Bkor not.Denef:
!Rby f(!) =(P(A\Bk)P(Bk);if!2BkandP(Bk)>0
c k;if!2BkandP(Bk) = 0;(10.1) whereck2Rcan be any constant. Now we dene the conditional probability, as a real-valued function on , by Pr(AjC)(!) =f(!). The following fact shows that our denition is reasonable in a way:P(A\Bk) =P(AjBk)P(Bk) =Z
B kPr(AjC)(!)dP(!): Now letCbe a generic sub--eld ofF. We can create a measureon ( ;C), given by (B) =P(A\B): If we can nd someC-measurable functionf, such that (Notice thatPis originally dened on ( ;F), but here we can treat it as a probability measure on ( ;C) asC F) (B) =P(A\B) =Z B f(!)dP(!); then we dene functionfto be theconditional probability ofAgivenC, and denote it asf= Pr(AjC). Thus by our denition 1)Pr( AjC)() isC-measurable.
2)8B2 C,(B) =P(A\B) =R
BPr(AjC)(!)dP(!).
RemarkThere exists manyversionsof Pr(AjC)(), but by property 2), these versions are equal to each othera:s:[P]. 10-110-2Lecture 10: March 1
LetX(!) =1A(!), then we may want to write
Pr(AjC) =E(XjC):
By generalizingXfrom an indicator function to any random variable we can get the denition of the conditional expectation.Denition 10.1.Given a probability space(
;F;P), letC Fbe a sub--eld ofF, andXanF=B- measurable random variable withEjXj<1. The conditional expectation ofXgivenCis any real valued functionh: !R, such that1)hisC-measurable.
2) RBh(!)dP(!) =R
BX(!)dP(!),8B2 C.
his denoted asE[XjC].Remark
f=E[XjC] meansfis a version ofE[XjC]. By 2) in the denition, ifh1andh2are two versions ofE[XjC], thenh1(!) =h2(!),a:s:[P]. Conversely, ifh1is a version ofE[XjC] andh1(!) =h2(!),a:s:[P], thenh2is also a version ofE[XjC].IfC=f?;
g, thenE[XjC] =E[X].IfXitself isC=Bmeasurable, thenX=E[XjC].
IfX=a; a:s:, thenE[XjC] =a; a:s:
10.1.1 Two perspectives
RN derivativeOne may ask "Does this function exist?". The answer is "Yes", and one can demonstrate this by usingRN derivative. AssumeX0; a:s:, the sketched proof is: dene(B) =RBX(!)dP(!), then
is a measure on ( ;C). By the RN theorem,9h, which isC-measurable and8B2 C, (B) =Z B h(!)dP(!): Then by denition, the RN derivativehis the conditional expectationE[XjC]. ProjectionAn alternative perspective is to think ofE[XjC] as a "projection". Given a r.v.Xon ( ;F;P) s.t.EX2<1andC F. ConsiderL2( ;C;P), a Hilbert space of r.v.'s that areC-measurable andL2. Then one can show that, theC-measurable random variableZis the conditional expectation ofXif and only ifZis the orthogonal projection ofXontoL2( ;C;P), that isE[W(XZ)] = 0;8W2L2(
;C;P); or equivalently,Z= argmin
W2L2( ;C;P)E(XW)2:Lecture 10: March 110-3
Now from this perspective, if we letC=(Y) whereYis an r.v. on ( ;F;P), then by theorem 39 in notes,E[XjY],E[XjC] = argmin
meas. functiong; s:t:E[g(Y)]2<1E(Xg(Y))2: Recall that the usual machinery of deningE[XjY] isE[XjY] =g(Y);whereg(y) =Z
R xfXjY(x;y)dy=Z
R xfX;Y(x;y)fY(y)dy:
Example 10.2.LetX1;X2i:i:d:Unifrom(0;1), andY= maxfX1;X2g,X=X1. Then one version ofE[XjY]ish(Y) =34
Y. In addition, another version can be given by
h1(Y) =(
34Y;ifYis irrational;
0;otherwise:
10.1.2 Properties
Some basic properties of conditional expectation coincide with expectation, including 1) Linearit y.If E[X],E[Y], andE[X+Y] all exist, thenE[XjC] +E[YjC] is a version ofE[X+YjC]. 2)Monotonicit y.If X1X2a:s:, thenE[X1jC]E[X2jC]a:s:
3) Jensen's in equality.Let E(X) be nite. Ifis a convex function and(X)2L1, thenE[(X)jMC] (E[XjC])a:s: 4) Con vergencetheorems: monotone con vergencetheorem, dominan tcon vergencetheorem. Theorem 10.3(Convergence theorem).LetCbe a sub--eld ofF. 1) (Monotone) If 0XnXa.s. for allnandXn!Xa.s., thenE[XnjC]!E[XjC]. 2) (Dominant) If Xn!Xa.s. andjXnj Ya.s., whereY2L1, thenE[XnjC]!E[XjC]. Proposition 10.4(Tower property of conditional expectation).If sub--eldsC1 C2 F, andEjXj<1, thenE[XjC1]is a version ofE[E[XjC2]jC1]. In particular,E[X] =E[E[XjC]](takingC=f?; g).10.2 Regular Conditional Probability
Notice that Pr(jC)() is a function dened onF
By denition, forA2 F, Pr(AjC)() is a version ofE[1AjC]().We would like8!2
, Pr(jC)(!) to be a probability measure on ( ;F). It is easy to see that Pr(AjC)()2[0;1]a:s:[P] as a function of!on ( ;C;P). We can also prove that it is countably additivea:e:[P]:10-4Lecture 10: March 1
Proposition 10.5.IffAng1n=1is a sequence of disjointF-measurable sets, thenW(!) =1X
n=1Pr(AnjC)(!) is a version ofPr(S1 n=1AnjC).This proposition means thatgivena sequence of disjointF-measurable setsfAng1n=1, for [P]a:e: !, we have
1 X n=1Pr(AnjC)(!) = Pr(1[ n=1A njC)(!): In general, however, for the collection of functionsfPr(AjC)()g:A2 Fgand agiven!2 , Pr(jC)(!) isnot necessarily countably additive, and therefore is not a probability measure. Even in the sense ofa:s:[P]
(with respect to!2 ), Pr(jC)(!) is not necessarily a probability measure. The intuition is, for a givenfAng1n=1of disjointF-measurable sets, to makeP1 n=1Pr(AnjC)(!) = Pr(S1 n=1AnjC)(!) (in the sense ofa:s:[P]), we can only allow Pr(S1 n=1AnjC)(!)6=P1 n=1Pr(AnjC)(!) for!in aP-measure-0 setN(fAng1n=1) Therefore, to make Pr(jC)(!) a probability measure (also in the sense ofa:s:[P]), we wantP(N(fAng1n=1)) = 0
to holda:s:[P] (w.r.t.!) over all possible choices of sequencefAng1n=1. To ensure this, We need P([ fAngN(fAng1n=1)) = 0:However, since there are uncountably many sequencesfAng1n=1, this may not necessarily hold. When this
nontrivial property holds, we call Pr(jC)() :A ![0;1] a regular conditional probability. Denition 10.6(Regular conditional probability).Given a probability space( ;F;P). LetA Fbe a sub--eld. We say that the functionPr(jC)() :A ![0;1]is a regular conditional probability (rcd) if1)8A2 A,Pr(AjC)()is a version ofE[1AjC].
2)F or[P]a:e: !2
,Pr(jC)(!)is a probability measure on( ;A).10.2.1 Regular Conditional Distribution
LetA=(X) for some r.v.Xthat isF=Bmeasurable. For eachB2 B, letXjC(B)(!) = Pr(X1(B)jC)(!):
Then functionXjC(jC)() :B
![0;1] is called a regular conditional distribution ofXgivenCwhen1)8B2 B,XjC(BjC)() is a version ofE[1X2BjC].
2)F or[ P]a:e: !2
,XjC(jC)(!) is a probability measure on (R;B).quotesdbs_dbs13.pdfusesText_19[PDF] indice brut 408 enseignant contractuel 2017
[PDF] indice de classement granulométrique
[PDF] indice de force de discipline
[PDF] indice de force ulaval 2015
[PDF] indice de force ulaval 2016
[PDF] indice de investigacion definicion
[PDF] indice de pulsatilidad doppler
[PDF] indice de resistencia renal
[PDF] indice de sensibilité exemple
[PDF] indice de un libro infantil
[PDF] indice de un proyecto de inversion
[PDF] indice de un proyecto definicion
[PDF] indice de un proyecto empresarial
[PDF] indice de un proyecto en word
