 Hauteur dun triangle et orthocentre
Hauteur dun triangle et orthocentre
La hauteur d'un triangle est une droite qui passe par un sommet du triangle et qui est perpendiculaire au côté opposé à ce sommet. Constructions. Pour
 HAUTEUR DANS LE TRIANGLE.pdf
HAUTEUR DANS LE TRIANGLE.pdf
L'aire du triangle ABC est de 575 cm². III) Orthocentre du triangle. Dans un triangle
 Droites et points remarquables dun triangle - Fiches de cours
Droites et points remarquables dun triangle - Fiches de cours
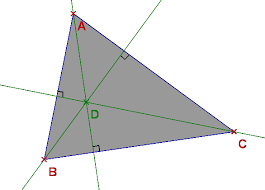
L'orthocentre est le point d'intersection des trois hauteurs d'un triangle. Dans un triangle une hauteur passe par un sommet et est perpendiculaire au côté ...
 Droites remarquables du triangle
Droites remarquables du triangle
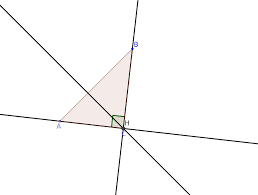
définition : On appelle hauteur d'un triangle une droite passant par un H est l'orthocentre du triangle. Triangle avec 3 angles aigus. Triangle avec ...
 LES DROITES REMARQUABLES DU TRIANGLE I. Les médiatrices
LES DROITES REMARQUABLES DU TRIANGLE I. Les médiatrices
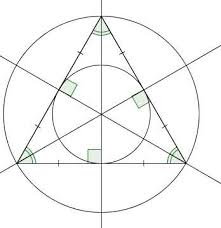
Leur point de concours est le centre du cercle circonscrit à ce triangle. II. Les hauteurs. Définition : Dans un triangle une hauteur est une droite qui passe
 Concours Général : Corrigé 2003 Composition de Maths
Concours Général : Corrigé 2003 Composition de Maths
(AH) est donc la hauteur issue de A et de même
 1. Dans le triangle ABC : a. Quelle est la hauteur issue de A ? (AE) b
1. Dans le triangle ABC : a. Quelle est la hauteur issue de A ? (AE) b
Quelle est la hauteur issue de C ? (CD) d. Quel est l'orthocentre du triangle ? H. 2. Dans le triangle BCH : a. Quelle est la hauteur relative à [BC] ? (AE).
 COMPOSITION DE MATH´EMATIQUES
COMPOSITION DE MATH´EMATIQUES
Calculer les coordonnées de l'orthocentre D du triangle ABC. 2. Soit X la sur la troisi`eme hauteur du triangle. Conclusion : les trois hauteurs sont ...
 Exercices autour de lorthocentre Exercices bonus
Exercices autour de lorthocentre Exercices bonus
5. Soit ABC un triangle d'orthocentre H. Soient M un point de de diamètre (AC) en K et L et la hauteur issue de C dans ABC intersecte le cercle de diamètre.
 _COURS ELEVE Droites remarquables
_COURS ELEVE Droites remarquables
Définition : Dans un triangle la hauteur issue d'un sommet est la droite qui passe par ce sommet et qui est perpendiculaire au côté opposé à ce sommet.
 Hauteur dun triangle et orthocentre
Hauteur dun triangle et orthocentre
La hauteur d'un triangle est une droite qui passe par un sommet du triangle et qui est perpendiculaire au côté opposé à ce sommet. Constructions. Pour
 Le concours des hauteurs dun triangle
Le concours des hauteurs dun triangle
Les hauteurs AB
 HAUTEUR DANS LE TRIANGLE.pdf
HAUTEUR DANS LE TRIANGLE.pdf
L'aire du triangle ABC est de 575 cm². III) Orthocentre du triangle. Dans un triangle
 Droites et points remarquables dun triangle - Fiches de cours
Droites et points remarquables dun triangle - Fiches de cours
L'orthocentre est le point d'intersection des trois hauteurs d'un triangle. S'il s'agit d'un triangle rectangle le centre du cercle circonscrit au ...
 _COURS ELEVE Droites remarquables
_COURS ELEVE Droites remarquables
Définition : Dans un triangle la hauteur issue d'un sommet est la droite qui passe par ce concourantes en un point appelé l'orthocentre.
 Longueurs des hauteurs médianes
Longueurs des hauteurs médianes
https://le-castillon.etab.ac-caen.fr/IMG/pdf/Longueurs_des_hauteurs_medianes_bissectrices_et_mediatrices_dans_un_triangle_rectangle_-_Correction.pdf
 -Réalisé par :
-Réalisé par :
Quelle est la hauteur relative à [BH] ? d. Quel est l'orthocentre du triangle ? Exercice 2 : 1) Construire un triangle IJK tel
 Droites remarquables du triangle
Droites remarquables du triangle
H est le point d'intersection des hauteurs du triangle. H est l'orthocentre du triangle. Triangle avec 3 angles aigus. Triangle avec un angle droit.
 Hyperbole et orthocentre ? ? = et lon note
Hyperbole et orthocentre ? ? = et lon note
toute légitimité que l'on peut parler du triangle On note ? la hauteur issue de du triangle ... l'orthocentre d'au moins un triangle. ; on peut.
 Modèle mathématique. Ne pas hésiter à consulter le fichier daide
Modèle mathématique. Ne pas hésiter à consulter le fichier daide
Prop: Dans un triangle les trois hauteurs sont concourantes en un point qui est appelé l'orthocentre du triangle. ! Rq Si le triangle est "aplati"
Le concours des hauteurs d'un triangle
Daniel PERRIN
Introduction
L'objectif de ce texte est de produire plusieurs
1demonstrations du concours
des hauteurs d'un triangle du plan euclidien2. On pourra estimer que cette
qu^ete de multiples preuves d'un theoreme bien connu est quelque peu vaine. Mais, d'abord, il s'agit d'un resultat qui n'est pas completement evident (la meilleure preuve est qu'il n'est pas dans Euclide) et il m'a paru utile de montrer comment on peut l'expliquer a divers niveaux de l'enseignement et notamment au college. Ensuite et surtout, mon objectif est d'illustrer le fait que plusieurs approches de la geometrie sont possibles et fructueuses, pourvu qu'elles s'appuient sur quelques principes simples. On verra notamment ici en action deux idees : l'utilisation des invariants elementaires (longueurs et angles) ou de leur variante algebrique (produit scalaire), le fait que les theoremes de geometrie proviennent des relations entre les invariants.0.1 Notations
On travaille dans le plan ane euclidienXet on considere un triangle abc(c'est-a-dire trois points non alignes). On noteA;B;Cles hauteurs du triangle, c'est-a-dire les perpendiculaires issues dea;b;caux c^otes (bc), (ca), (ab) respectivement eta0;b0;c0leurs pieds, c'est-a-dire les intersections de A;B;Cavec les c^otes (bc), (ca) et (ab). Le theoreme en vue est alors :0.1 Theoreme.Les hauteursA;B;Csont concourantes en un pointhappele
orthocentredu triangleabc.0.2 Preliminaire : deux hauteurs se coupent
Dans presque toutes les preuves nous utiliserons le lemme suivant :0.2 Lemme.Les hauteursB;Cse coupent en un pointh.
Demonstration.Il s'agit de montrer queB;Cne sont pas paralleles. On rai- sonne par l'absurde. SiB;Csont paralleles, comme (ac) est perpendiculaire aBelle est aussi perpendiculaire aC(ici, on utilise de maniere essentielle1. Neuf pour l'instant.2. Pour le cas non euclidien, voir [DP] Partie IV.
1 le postulat d'Euclide3sous la forme de l'egalite des angles alternes-internes
par exemple). Comme (ab) est aussi perpendiculaire aCon en deduit que (ab) et (ac) sont paralleles, ce qui est absurde (ici on n'utilise pas le postulat d'Euclide).1 Les preuves elementaires
1.1 La preuve classique
A B C a b c f e dFigure1 { La preuve classique Elle consiste a ramener le concours des hauteurs a celui des mediatrices, qui est beaucoup plus simple. On considere les droitesA0;B0;C0, respecti- vement paralleles a (bc) passant para, a (ca) parbet a (ab) parc. Elles se coupent end;e;f(voir gure 1). Les pointsa;b;csont les milieux des c^otes du triangledef. En eet, les quadrilateresafbcetaecbsont des pa- rallelogrammes et on a doncaf=bc=ae. Par ailleurs, les droitesA;B;C sont perpendiculaires a (ef), (fd) et (de) respectivement (car elles sont per- pendiculaires a des droites paralleles a celles-ci). On en deduit queA;B;Csont les mediatrices dedef, d'ou leur concours.3. Et cette propriete est en defaut en geometrie hyperbolique, voir sur ma page web la
Partie IV de mon projet de livre de geometrie projective [DP]. 21.2 La preuve par les angles
1.2.1 Introduction
J'aime beaucoup cette preuve, pour trois raisons. D'abord, parce que je ne l'ai jamais rencontree nulle part4. Ensuite parce qu'elle est conforme a la
theorie, inspiree du programme d'Erlangen, qui dit que tout theoreme d'une geometrie relative a un certain groupe doit pouvoir se montrer en utilisant les invariants de ce groupe. Ici, le groupe est celui des similitudes et l'invariant est l'angle. Enn, corollaire de ce point, parce qu'elle illustre bien la doctrine didactique que je preconise s'agissant des angles : pour les utiliser il faut employer quatre types d'accessoires : les notions de complementaires et supplementaires, la somme des angles du triangle, les theoremes lies au parallelisme (alternes-internes, etc.), et enn, le theoreme de l'angle inscrit. Hormis le troisieme point, tous sont a l'uvre ici, directement ou non.1.2.2 Quadrilateres inscriptibles Figure2 { Quadrilateres inscriptibles
Nous utiliserons le theoreme de l'angle inscrit par le biais des quadrilateres inscriptibles, avec les deux types de gures remarquables ci-dessus, toutes deux formees de triangles rectangles inscrits dans un demi-cercle et accolespar leur hypotenuse, dans un cas de part et d'autre et dans l'autre du m^eme4. Comme me l'a signale Sylvain Baron, le ressort de cette preuve est le m^eme que celui
qui permet de prouver la propriete classique du triangle orthique : les hauteurs deabcsont les bissectrices du triangle forme par les pieds des hauteurs. 3 c^ote. L'existence de ces triangles montre que les points sont cocycliques et on en deduit l'egalite des angles interceptant le m^eme arc.1.2.3 Le theoreme
On appellehl'intersection deBetCet on montre que (ah) est perpendi- culaire a (bc). Il sut pour cela de montrer que les angles=dbahetbb=cabc sont complementaires. Mais, le quadrilatereac0hb0est inscriptible (a cause des angles droits enb0etc0). On a donc=dc0b0h. De m^emebcb0c0est ins- criptible, toujours a cause des m^emes angles droits, mais vus de l'autre c^ote. On a doncdc0b0h=dc0cb. Mais il est clair quedc0cbetbbsont complementaires et on a gagne. B C a b c b' c' hFigure3 { La preuve par les angles1.3 La preuve par les longueurs
La encore, il s'agit d'une preuve utilisant les invariants euclidiens, ici les longueurs.Le lemme crucial est le suivant :
1.1 Lemme.Le pointmest sur la hauteurAissue deasi et seulement si
on amb2mc2=ab2ac2. Demonstration.Supposons quemest sur la hauteur. On applique Pythagore avec les angles droits ena0et on amb2=ma02+a0b2,mc2=ma02+a0c2, 4 d'oumb2mc2=a0b2a0c2. Mais cette relation vaut en particulier pour m=a, d'ou l'egalite cherchee. a b c a' m a b c a' m m'Figure4 { La preuve par les longueurs Reciproquement, si on a l'egalite, on introduit le projete orthogonalm0de msur (bc). Il s'agit de montrer qu'on am0=a0. Une nouvelle application de Pythagore donnem0b2m0c2=a0b2a0c2, ou encore (m0bm0c)(m0b+m0c) = (a0ba0c)(a0b+a0c). Traitons d'abord le cas oua0etm0sont tous deux interieurs a [bc]. On a alorsm0a+m0b=a0b+a0c=bcet on en deduit m0bm0c=a0ba0c, donc, avec les deux equations,m0b=a0betm0c=a0c
donca0=m0. En fait, la position n'a pas d'importance car on a le lemme :1.2 Lemme.Soientb;cdeux points distincts etp;q2(bc)veriantpb2
pc2=qb2qc2. Alors, on ap=q.
Demonstration.(du lemme 1.2) On a(p) :=pb2pc2= (pbpc)(pb+pc) et cette quantite est du signe depbpc. Comme les deux quantites(p) et(q) ont m^eme signe,petqsont tous deux soit plus pres decsoit deb, disons dec:pbpcetqbqc. Sipest interieur a [bc] on apb+pc=bcet pbpcbc, donc(p)bc2, tandis que sipest exterieur, on apbpc=bc etb+pcbc, donc(p)bc2. Commeest le m^eme pourpetq, on voit qu'ils sont tous deux interieurs ou tous deux exterieurs. Dans les deux cas on en deduitpbpc=qbqcetpb+pc=qb+qcdonc, par addition,pb=qb etpc=qc, doncp=q(par exemple parce que les positions depetqpar rapport ab;csont les m^emes). On peut alors nir la preuve de 0.1. Soithle point d'intersection des hauteursBetC. D'apres le sens direct de 1.1 on aha2hb2=ca2cb2et 5 ha2hc2=ba2bc2. Par dierence on en deduithb2hc2=ab2ac2et
on conclut par le sens reciproque de 1.1.1.4 La preuve qui annonce la droite d'Euler
o a b c h p c' b' m gFigure5 { La droite d'Euler en prime On considere les hauteurs issues debetcqui se coupent enh. Il s'agit de montrer que (ah) est perpendiculaire a (bc). Pour cela, on introduit le cercle circonscrit au triangleabc, centre eno. On appelleple point diametralement oppose aasur . Les trianglesapbetapc, inscrits dans des demi-cercles, sont rectangles enbetc, donc les droites (pb) et (ab) (resp. (pc) et (ac)) sont perpendiculaires et donc (pb) et (pc) sont respevtivement paralleles aux hauteurs (ch) et (bh). Il en resulte quebhcpest un parallelogramme, donc ses diagonales [ph] et [bc] se coupent en leur milieum. Dans le triangleahp, la droite (om) est une droite des milieux, donc parallele a (ah). Il sut donc de montrer que (om) est perpendiculaire a (bc). Mais (om) est la mediane du triangleobc, qui est isocele eno. C'est donc aussi la hauteur et on a gagne5.1.3Remarque.La gure ci-dessus mene aussi a la propriete de la droite
d'Euler deabc. On considere encore le triangleahp, dont [ho] et [am] sont des medianes. Elles se coupent donc eng, centre de gravite deahp, situe autiers de [am] a partir dem. Mais, comme [am] est aussi la mediane deabc, le5. Je remercie Gerald Forhan de m'avoir soue cette preuve.
6 pointgest le centre de gravite deabc. On voit ainsi queo;g;hsont alignes et, de plus, avec la mediane [ho] deahp, on a l'egalitehg= 2go.2 Les preuves utilisant le produit scalaire
2.1 Theoremes et relations
La premiere preuve est une magnique illustration du principe, deja evoque ci-dessus : les theoremes proviennent des relations entre invariants. Ici, l'invariant est le produit scalaire et on a une relation triviale :2.1 Lemme.Soienta;b;c;hquatre points deX. On a la relation :
!haj!bc) + (!hbj!ca) + (!hcj!ab) = 0:Demonstration.Il sut de faire appara^trehenecrivant la relation de Chasles!bc=!bh+!hcet de m^eme pour les autres et d'utiliser la bilinearite et la
symetrie du produit scalaire. On en deduit 0.1. On applique la relation en prenant pourhl'intersection deBetC. Les deux derniers produits scalaires sont nuls, donc aussi le premier, ce qui montre que la droite (ha) est perpendiculaire a (bc), donc est la hauteurA.2.2 Delit d'initie
On montre le lemme suivant :
2.2 Lemme.Soitole centre du cercle circonscrit aabcet soithle point
deni par la formule :!oh=!oa+!ob+!oc. Alorshest sur les trois hauteurs. Demonstration.Montrons par exemple quehest sur la hauteur issue dea, i.e. qu'on a (!ahj!bc) = 0. On ecrit!ah=!ao+!oh=!ob+!ocet!bc=!oc!ob et on en deduit (!ahj!bc) = (!ob+!ocj!oc!ob) =oc2ob2= 0 puisqueoest le centre du cercle circonscrit.quotesdbs_dbs17.pdfusesText_23[PDF] HAUTEUR Masculin MINIME - Anciens Et Réunions
[PDF] Hauteur Midi - hauteur tempérée - fréquence MIDI Pitch - Cigares
[PDF] HAUTEUR PURE MINI ET POUSSINS Club- Nom
[PDF] have not yet been appointed may also be sent to the Geneva
[PDF] Have you ever heard of an endangered species
[PDF] Have You Ever Seen The Rain - Anciens Et Réunions
[PDF] Have You Ever Seen The Rain - Si, Seniors - Anciens Et Réunions
[PDF] Have You Ever Seen the Rain L – 18 décembre 2013 - Anciens Et Réunions
[PDF] Have you ever seen the rain – Dr
[PDF] Have YOU thought about... Avez-vous pensé à - Anciens Et Réunions
[PDF] Have/Want - LandAndInvestment.com - Anciens Et Réunions
[PDF] HAVEP® ATTITUDE
[PDF] HAVING FUN IN ENGLISH
[PDF] Havoc XT Safety Data Sheet - Des Gants
