 TD 3 : Méta-heuristiques Exercice 1 (1/1)
TD 3 : Méta-heuristiques Exercice 1 (1/1)
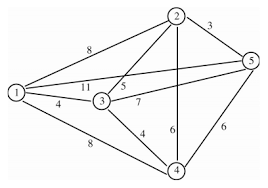
12/01/2014 Exercice 1 (1/1). Janvier 2014. RCP104 – Optimisation en Informatique. 2. Considérez le problème de voyageur de commerce représenté par le ...
 Métaheuristiques : Recherches locales et Algorithmes
Métaheuristiques : Recherches locales et Algorithmes
12/10/2012 Métaheuristiques. Page 41. Métaheuristiques standards. Paysage Adaptatif. Un exemple très simple. Exercice. Coder la recherche locale aléatoire.
 Examens et corrigés-type doptimisation combinatoire Pour les
Examens et corrigés-type doptimisation combinatoire Pour les
7) Ecrire un algorithme général d'une métaheuristique à population de solutions. Exercice 2 (07 pts). Un carré magique d'ordre n est une matrice carrée n×n
 Exercice 1
Exercice 1
On envisage de résoudre le problème à l'aide d'une méta-heuristique : le recuit-simulé. La première étape de cette méthode consiste à déterminer une
 Questions de cours (6.50 points) Exercice N°02 : modélisation (6.50
Questions de cours (6.50 points) Exercice N°02 : modélisation (6.50
3- Avec les métaheuristiques nous avons la garantie de trouver une solution exacte pour un problème Faux : car la recherche tabou a été introduite pour ...
 ésolution de problèmes di4ciles : algorithmes dGapproximationT
ésolution de problèmes di4ciles : algorithmes dGapproximationT
V oir exercices. 1.3 Exemple : identifier le plus Le chapitre sur le voyageur de commerce présente un algorithme (plus précisément une métaheuristique) ...
 [tel-00011623 v1] Métaheuristiques : Stratégies pour loptimisation
[tel-00011623 v1] Métaheuristiques : Stratégies pour loptimisation
Loin d'être un recueil d'exercices corrigés ce livre est en fait auto-contenu grâce `a deux chapitres de cours sur les bases théoriques de la programmation
 Optimisation et Recherche opérationelle Exercice 1 : Exercice 2 :
Optimisation et Recherche opérationelle Exercice 1 : Exercice 2 :
— Le barème donné est indicatif. Exercice 1 : Question de cours (2 pts). Donner le nom de trois algorithmes métaheuristiques vus en cours. Parmi ceux-ci
 Perfectionnement de métaheuristiques pour loptimisation continue
Perfectionnement de métaheuristiques pour loptimisation continue
07/04/2014 ... corrigée de la façon suivante : Xij
 Annexe au chapitre 9 Métaheuristiques
Annexe au chapitre 9 Métaheuristiques
On répétera cet algorithme des milliers de fois et on n'affichera que la meilleure solution trouvée. Programmez cet algorithme en Python. Exercice A9.4. Takeshi
 Métaheuristiques
Métaheuristiques
Exercice. Recherche arborescente pour le TSP (exemple A*) Une métaheuristique est un principe générique à adapter pour chaque problème.
 ésolution de problèmes di4ciles : algorithmes dGapproximationT
ésolution de problèmes di4ciles : algorithmes dGapproximationT
4.5 Quelques exemples d'applications des métaheuristiques . 4.6 Caractéristiques communes aux diverses métaheuristiques . ... V oir exercices.
 Métaheuristiques : Recherches locales et Algorithmes
Métaheuristiques : Recherches locales et Algorithmes
12?/10?/2012 Exercice. Coder dans le langage que vous voulez
 Annexe au chapitre 9 Métaheuristiques
Annexe au chapitre 9 Métaheuristiques
On répétera cet algorithme des milliers de fois et on n'affichera que la meilleure solution trouvée. Programmez cet algorithme en Python. Exercice A9.4. Takeshi
 Exercice N°01 : Questions de cours (6.50 points) Exercice N°02
Exercice N°01 : Questions de cours (6.50 points) Exercice N°02
«ORO: Optimisation en Recherche Opérationnelle» Solution d'Examen final Durée : 3- Avec les métaheuristiques nous avons la garantie de trouver une ...
 Examens et corrigés-type doptimisation combinatoire Pour les
Examens et corrigés-type doptimisation combinatoire Pour les
algorithmes : PSO ACO
 LICENCE 3 MATHEMATIQUES – INFORMATIQUE
LICENCE 3 MATHEMATIQUES – INFORMATIQUE
Exercices proposés (avec corrigés) : 117 (exemple) 118 (algorithme du gradient à pas optimal) et 119 (Jacobi et optimisation). Semaine 3 :.
 Optimisation et Recherche opérationelle Exercice 1 : Exercice 2 :
Optimisation et Recherche opérationelle Exercice 1 : Exercice 2 :
Cet examen comporte trois exercices indépendants pouvant être traités dans n'importe Donner le nom de trois algorithmes métaheuristiques vus en cours.
 TD 3 : Méta-heuristiques Exercice 1 (1/1)
TD 3 : Méta-heuristiques Exercice 1 (1/1)
12?/01?/2014 Exercice 1 (1/1). Janvier 2014. RCP104 – Optimisation en Informatique. 2. Considérez le problème de voyageur de commerce représenté par le ...
 Métaheuristiques: Stratégies pour loptimisation de la production de
Métaheuristiques: Stratégies pour loptimisation de la production de
15?/02?/2006 dans les métaheuristiques ou dans la programmation linéaire. Ce programme est ... Loin d'être un recueil d'exercices corrigés.
 Métaheuristiques : Recherches locales et Algorithmes
Métaheuristiques : Recherches locales et Algorithmes
>Métaheuristiques : Recherches locales et Algorithmes https://www-lisic univ-littoral fr/ /12-13/sac-M1/metaheuristiques pdf · Fichier PDF
 Les méthodes Métaheuristiques
Les méthodes Métaheuristiques
>Les méthodes Métaheuristiques
 Méta-Heuristiques - LAAS
Méta-Heuristiques - LAAS
>Méta-Heuristiques - LAAS
 Méthodes de descente Problèmes sans contraintes
Méthodes de descente Problèmes sans contraintes
>Méthodes de descente Problèmes sans contrainteshttps://www math univ-paris13 fr/ /teaching/MACS2_2019/Polych · Fichier PDF
Qu'est-ce que les métaheuristiques?
Les métaheuristiques constituent une classe de méthodes qui fournissent des solutions de bonne qualité en temps raisonnable à des problèmes combinatoires réputés difficiles pour lesquels on ne connaît pas de méthode classique plus efficace.
Quels sont les différents types de métaheuristique?
La métaheuristique manipule un ensemble de solutions en parallèle, à chaque itération. On peut citer les algorithmes génétiques, l’ optimisation par essaims particulaires, les algorithmes de colonies de fourmis. La frontière est parfois floue entre ces deux classes.
Quelle est la différence entre une heuristique et une métaheuristique?
?processus de génération qui guide une heuristique ?en combinant des concepts différents pour explorer l’espace de recherche afin de trouver efficacement des solutions quasi optimales ?Une métaheuristique est un principe générique à adapter pour chaque problème 21 Heuristique versus Métaheuristique (2)
LICENCE 3 MATHEMATIQUES - INFORMATIQUE.
MATHEMATIQUES GENERALES.
L3MiMG.
Expédition dans la semaine n°EtapeCode UEN° d'envoi de l'UE92L3MATSMI5U4T5
Nom de l'UE : Analyse numériqueet optimisation
Le cours contient 3 chapitres (systèmes linéaires, systèmes non linéaires, optimisation). Pour chaque semaine, il est
proposé d'étudier une partie du cours, de faire des exercices (corrigés) et, éventuellement, de réaliser un TP en
python. Les TP sont fortement conseillés mais non obligatoires. Deux devoirs sont à rendre afin de bénéficier d'une
note de contrôle continu. note finale=max(note-examen, 1/3(2 note-examen + note-contrôle-continu)). - Contenu de l'envoi : Polycopié, chapitre 3 (optimisation) - Guide du travail à effectuerSemaine 1 :
Etudier les paragraphes 3.1 et 3.2 (optimisation sans contrainte) et 3.4 (optimisation avec contrainte)
Ces paragraphes font aussi partie du cours de calcul différentiel et optimisationExercices proposés (avec corrigés) :
110 (exemples), 112 (fonctions quadratiques) et 115 (complément de Schur)
Semaine 2 :
Etudier les paragraphes 3.3.1 (méthodes de descente) et 3.3.2 (algorithme du gradient conjugué, GC)
Exercices proposés (avec corrigés) :
117 (exemple), 118 (algorithme du gradient à pas optimal) et 119 (Jacobi et optimisation)
Semaine 3 :
Etudier le paragraphe 3.3.3 (Newton)
Exercice proposé (avec corrigé) : 127 (Polak-Ribière)Semaine 4 :
Etudier les paragraphe 3.4 et 3.5 (optimisation avec contrainte) Exercice proposé (avec corrigé) : 139 (Uzawa)Le corrigé du deuxième devoir sera, à la fin du mois de mars, sur le site du télé-enseignement et sur
site web indiqué ci-dessous-Coordonnées de l'enseignant responsable de l'envoi T. Gallouet, CMI, 39 rue Joliot Curie, 13453 marseille cedex 13 email : thierry.gallouet@univ-amu.fr Vous pouvez aussi consulter la page web:http://www.i2m.univ-amu.fr/~gallouet/tele.d/anum.d et me poser des questions par emailA i x M a r s e i l l e U n i v e r s i t é - C e n t r e d e T é l é - E n s e i g n e m e n t S c i e n c e sCase 35. 3, place Victor Hugo. 13331 Marseille Cedex 03.
http://www.ctes.univ-provence.fr P o u r r a p p r o c h e r l a c o n n a i s s a n c eChapitre 3Optimisation3.1 Définitions et rappels3.1.1 Extrema, points critiques et points selle.L"objectif de ce chapitre est de rechercher des extrema, c"est-à-dire des minima ou des maxima d"une fonction
f?C(IRn,IR)avec ou sans contrainte. Notons que la recherche d"un minimum ou d"un maximum implique que
l"on ait une relation d"ordre, pour pouvoir comparer les valeurs prises parf. On insiste donc bien sur le fait que
la fonctionfest à valeurs dansIR(et non pasIRn, comme dans le chapitre précédent). Rappelons tout d"abord
quelques définitions du cours de calcul différentiel. Définition 3.1(Extremum d"une fonction).SoitEun espace vectoriel normé etf:E→IR. On dit que¯xest un minimum local defs"il existe un voisinageVde¯xtel que De même, on dit que¯xest un maximum local defs"il existe un voisinageVde¯xtel que f(¯x)≥f(x),?x?V. On dit que¯xest un extremum local defsi c"est un minimum local ou un maximum local.On dit que¯xest un minimum global defsi
De même, on dit que¯xest un maximum global defsi f(¯x)≥f(x),?x?E. On dit que¯xest un extremum global defsi c"est un minimum global ou un maximum global. Le problème d"optimisation sans contrainte s"écrit : ?Trouver¯x?IRntel que : Le problème d"optimisation avec contrainte s"écrit : ?Trouver¯x?Ktel que : 2073.1. DÉFINITIONS ET RAPPELSCHAPITRE 3. OPTIMISATION
oùK?IRnetK?= IRnL"ensembleKoù l"on recherche la solution est donc l"ensemble qui représente les
contraintes. Par exemple, si l"on cherche un miminum d"une fonctionfdeIRdansIRet que l"on demande que les
points qui réalisent ce minimum soient positifs, on auraK= IR+.Si¯xest solution du problème (3.1), on dit que¯x?argminIRnf, et si¯xest solution du problème (3.2), on dit que
¯x?argminKf.
Vous savez déjà que si un point¯xréalise le minimum d"une fonctionfdérivable deIRdansIR, alorsf?(
x) = 0.On dit que c"est un point critique (voir définition 3.2). La réciproque est évidemment fausse : la fonctionx?→x3
est dérivable surIR, et sa dérivée s"annule en 0 qui est donc un point critique, mais 0 n"est pas un extremum (c"est
un point d"inflexion).Nous verrons plus loin que de manière générale, lorsque la fonctionnellefest différentiable,
les extrema sont des points critiques def, au sens où ils annulent le gradient.Définition 3.2(Point critique).SoitEun espace vectoriel normé etf:E→IRdifférentiable. On dit quex?E
est un point critique defsiDf(x) = 0. Pour illustrer un cas de point critique qui n"est pas un maximum ni un minimum, prenons un exemple en dimension 2, avec f(x1,x2) =x21-x22.On a alors
Df(x1,x2)(h1,h2) = 2(x1h1-x2h2)etDf(0,0) = 0.
Le point(0,0)est donc un point critique def. Si on trace la surface x?→x21-x22, on se rend compte que le point(0,0)est minimal dans une direction et maximal dans une direction indépendante de la première. C"est ce qu"on appelle un point selleDéfinition 3.3(Point selle).SoitEun espace vectoriel normé etf:E→IR. On dit que¯xest un point selle def
s"il existeFetGdes sous espaces vectoriels deEtels queE=F?Get un voisinageVde¯xtel que f(¯x+z)≥f(¯x),?z?G; ¯x+z?V.3.1.2 Convexité
Définition 3.4(Convexité).SoitEun espace vectoriel (surIR) etf:E→IR. On dit quefest convexe si
On dit quefest strictement convexe si
f(tx+ (1-t)y)< tf(x) + (1-t)f(y)pour tout(x,y)?E2t.q.x?=yett?]0,1[.Proposition 3.5(Première caractérisation de la convexité).SoitEun espace vectoriel normé (surIR) etf?
C1(E,IR)alors :
Analyse numérique I, télé-enseignement, L3208Université d"Aix-Marseille, R. Herbin, 29 janvier 2018
3.1. DÉFINITIONS ET RAPPELSCHAPITRE 3. OPTIMISATION
1. la fonctionfest convexe si et seulement sif(y)≥f(x) +Df(x)(y-x), pour tout couple(x,y)?E2,
2. la fonctionfest strictement convexe si et seulement sif(y)> f(x) +Df(x)(y-x)pour tout couple
(x,y)?E2tel quex?=y.DÉMONSTRATION-Démonstration de 1.
(?) Supposons quefest convexe : soit(x,y)?E2; on veut montrer quef(y)≥f(x) +Df(x)(y-x). Soitt?[0,1],
Commefest différentiable,f(x+t(y-x)) =f(x) +Df(x)(t(y-x)) +tε(t)oùε(t)tend vers 0 lorsquettend vers
0. Donc en reportant dans (3.3),
En faisant tendretvers 0, on obtient alors :
f(y)≥Df(x)(y-x) +f(x).(?) Montrons maintenant la réciproque : Soit(x,y)?E2, ett?]0,1[(pourt= 0ou= 1on n"a rien à démontrer). On
f(y)≥f(z) +Df(z)(y-z), etf(x)≥f(z) +Df(z)(x-z).En multipliant la première inégalité par1-t, la deuxième partet en les additionnant, on obtient :
(1-t)f(y) +tf(x)≥f(z) + (1-t)Df(z)(y-z) +tDf(z)(x-z) (1-t)f(y) +tf(x)≥f(z) +Df(z)((1-t)(y-z) +t(x-z)). Et comme(1-t)(y-z) +t(x-z) = 0, on a donc(1-t)f(y) +tf(x)≥f(z) =f(tx+ (1-t)y).Démonstration de 2
(?) On suppose quefest strictement convexe, on veut montrer quef(y)> f(x) +Df(x)(y-x)siy?=x. Soit donc
(x,y)?E2,x?=y. On posez=12(y-x), et commefest convexe, on peut appliquer la partie 1. du théorème et écrire
quef(x+z)≥f(x) +Df(x)(z).On a doncf(x) +Df(x)(y-x entraîne quef(x) +Df(x)(y-x2)<12(f(x) +f(y)), d"où le résultat.
(?) La méthode de démonstration est la même que pour le 1. Proposition 3.6(Seconde caractérisation de la convexité).SoitE= IRnetf?C2(E,IR). SoitHf(x)la hessienne defau pointx, i.e.(Hf(x))i,j=∂2i,jf(x). Alors1.fest convexe si et seulement siHf(x)est symétrique et positive pour toutx?E(c.à.d.Hf(x)t=Hf(x)
etHf(x)y·y≥0pour touty?IRn)2.fest strictement convexe siHf(x)est symétrique définie positive pour toutx?E. (Attention la réciproque
est fausse.)DÉMONSTRATION-Démonstration de 1.
(?) Soitfconvexe, on veut montrer queHf(x)est symétrique positive. Il est clair queHf(x)est symétrique car∂2i,jf=
2j,ifcarfestC2. Par définition,Hf(x) =D(?f(x))et?f?C1(IRn,IRn).Soit(x,y)?E2, commefest convexe
et de classeC1, on a, grâce à la proposition 3.5 : f(y)≥f(x) +?f(x)·(y-x).(3.4) Soit??C2(IR,IR)définie par?(t) =f(x+t(y-x)).Alors : f(y)-f(x) =?(1)-?(0) =? 1 0 ??(t)dt= [??(t)(t-1)]10-? 1 0 ???(t)(t-1)dt, c"est-à dire :f(y)-f(x) =??(0) +?10???(t)(1-t)dt.Or??(t) =?f(x+t(y-x))·(y-x),et
??(t) =D(?f(x+t(y-x))(y-x)·(y-x) =Hf(x+t(y-x))(y-x)·(y-x).On a donc :
f(y)-f(x) =?f(x)(y-x) +? 1 0 H f(x+t(y-x))(y-x)·(y-x)(1-t)dt.(3.5)Analyse numérique I, télé-enseignement, L3209Université d"Aix-Marseille, R. Herbin, 29 janvier 2018
3.1. DÉFINITIONS ET RAPPELSCHAPITRE 3. OPTIMISATION
Les inégalités (3.4) et (3.5) entraînent :?10Hf(x+t(y-x))(y-x)·(y-x)(1-t)dt≥0?x,y?E. On a donc :?
1 0 H f(x+tz)z·z(1-t)dt≥0?x,?z?E.(3.6) En fixantx?E, on écrit (3.6) avecz=εy,ε >0,y?IRn. On obtient : 2? 1 0 H f(x+tεy)y·y(1-t)dt≥0?x,y?E,?ε >0,et donc : 1 0Hf(x+tεy)y·y(1-t)dt≥0?ε >0.
Pour(x,y)?E2fixé,Hf(x+tεy)tend versHf(x)uniformément lorsqueε→0, pourt?[0,1]. On a donc :?1
0 H f(x)y·y(1-t)dt≥0,c.à.d.12Hf(x)y·y≥0.
Donc pour tout(x,y)?(IRn)2,Hf(x)y·y≥0doncHf(x)est positive.(?) Montrons maintenant la réciproque : On suppose queHf(x)est positive pour toutx?E. On veut démontrer que
fest convexe; on va pour cela utiliser la proposition 3.5 et montrer que :f(y)≥f(x) +?f(x)·(y-x)pour tout
(x,y)?E2. Grâce à (3.5), on a : f(y)-f(x) =?f(x)·(y-x) +? 1 0 H f(x+t(y-x))(y-x)·(y-x)(1-t)dt.OrHf(x+t(y-x))(y-x)·(y-x)≥0pour tout couple(x,y)?E2, et1-t≥0sur[0,1]. On a doncf(y)≥
f(x) +?f(x)·(y-x)pour tout couple(x,y)?E2. La fonctionfest donc bien convexe.Démonstration de 2.
(?) On suppose queHf(x)est strictement positive pour toutx?E, et on veut montrer quefest strictement convexe.
On va encore utiliser la caractérisation de la proposition 3.5. Soit donc(x,y)?E2tel quey?=x. Alors :
f(y) =f(x) +?f(x)·(y-x) +? 1 0 H f(x+t(y-x))(y-x)·(y-x)? >0six?=y(1-t)???? ?=0sit?]0,1[dt. Doncf(y)> f(x) +?f(x)(y-x)six?=y, ce qui prouve quefest strictement convexe.Contre-exemplePour montrer que la réciproque de 2. est fausse, on propose lecontre-exemple suivant : Soit
n= 1etf?C2(IR,IR), on a alorsHf(x) =f??(x). Sifest la fonction définie parf(x) =x4, alorsfest strictement convexe maisf??(0) = 0.3.1.3 Exercices (extrema, convexité)
Exercice 110(Vrai / faux).corrigé en page 212
1. L"applicationx?→ ?x?∞est convexe surIR2.
2. L"applicationx?→ ?x?∞est strictement convexe surIR2.
3. L"application deIR2dansIRdéfinie parF(x,y) =x2-2xy+ 3y2+yadmet un unique minimum.
4. SoitA?Mn,m(IR),b?IRn, l"applicationx?→ ?Ax-b?2admet un unique minimum.
Exercice 111(Minimisation dansIR).Corrigé en page 212 OnconsidèrelesfonctionsdéfiniesdeIRdansIRparf0(x) =x2,f1(x) =x2(x-1)2,f2(x) =|x|,f3(x) = cosx, f4(x) =|cosx|,f5(x) =ex. On poseK= [-1,1]. Pour chacune de ces fonctions, répondre aux questions
suivantes :1. Etudier la différentiabilité et la (stricte) convexité éventuelles de la fonction,; donner l"allure de son graphe.
2. La fonction admet elle un minimum global surIR; ce minimum est-il unique? Le cas échéant, calculer ce
minimum.Analyse numérique I, télé-enseignement, L3210Université d"Aix-Marseille, R. Herbin, 29 janvier 2018
3.1. DÉFINITIONS ET RAPPELSCHAPITRE 3. OPTIMISATION
3. LafonctionadmetelleunminimumsurK; ceminimumest-ilunique?Lecaséchéant,calculerceminimum.
Exercice 112(Fonctions quadratiques).
1. Montrer que la fonctionfdeIR2dansIRdéfinie parf(x,y) =x2+ 4xy+ 3y2n"admet pas de minimum
en(0,0).2. Trouver la matrice symétriqueStelle quef(x) =xtSx, pourf1(x) = 2(x21+x22+x23-x1x2-x2x3),
puis pourf2(x) = 2(x21+x22+x23-x1x2-x1x3-x2x3)Etudier la convexité des fonctionsf1etf2.3. Calculerles matriceshessiennesdeg1etg2définiespar:g1(x,y) =1
4x4+x2y+y2etg2(x,y) =x3+xy-x
et étudier la convexité de ces deux fonctions. Exercice 113(Convexité et continuité).Suggestions en page 211.1. Soitf: IR→IRune fonction convexe.
(a) Montrer quefest continue. (b) Montrer quefest localement lipschitzienne.2. Soitn≥1etf: IRn→IR. On suppose quefest convexe.
m Rsi la norme dexest inférieure ou égale àR). (b) Montrer quefest continue. (c) Montrer quefest localement lipschitzienne.(d) On remplace maintenantIRnparE, e.v.n. de dimension finie. Montrer quefest continue et quefest locale-
ment lipschitzienne.3. SoientEun e.v.n. de dimension infinie etf:E→IR. On suppose quefest convexe.
(a) On suppose, dans cette question, quefest bornée supérieurementsur les bornés. Montrer quefest continue.
(b) Donner un exemple d"e.v.n. (notéE) et de fonction convexef:E→IRt.q.fsoit non continue.Suggestions pour les exercices
Exercice 113 page 211 (Convexité et continuité)1.(a) Pour montrer la continuité en0, soitx?= 0,|x|<1. On posea=sgn(x) (=x
|x|). Ecrirexcomme une combinaison convexe de0etaet écrire0comme une combinaison convexe dexet-a. En déduire une majoration de|f(x)-f(0)|. (b) Utiliser la continuité defet la majoration précédente.2.(a) Faire une récurrence surnet pourx= (x1,y)tavec-R < x1< Rety?IRn-1(n >1), majorerf(x)en
utilisantf(+R,y)etf(-R,y). (b) Reprendre le raisonnement fait pourn= 1. (c) Se ramener àE= IRn.3.(a) reprendre le raisonnement fait pourE= IR.
(b) On pourra, par exemple choisirE=C([0,1],IR)...Analyse numérique I, télé-enseignement, L3211Université d"Aix-Marseille, R. Herbin, 29 janvier 2018
3.2. OPTIMISATION SANS CONTRAINTE CHAPITRE 3. OPTIMISATION
Corrigés des exercices
Exercice 110 page 210 (Minimisation dansR)
1. Vrai.
2. Faux. L"application est convexe mais pas strictement convexe. Si on fixev1= (1,0)etv2= (1,1), alors
pour toutt?[0,1], ?tv1+ (1-t)v2?∞=?(1,1-t)?∞= 1 =t?v1?∞+ (1-t)?v2?∞.3. Vrai. PosonsX= (x,y)t, on reconnait la fonctionnelle quadratiqueF(x,y) =1
2(AX,X)-(b,X)avec
A=?1-1
-1 3? etb=?01? . La matriceAune matrice symétrique définie positive. Le cours nous dit alors queFadmet un unique minimum.4. Contre-exemple. SoitA=?1 00 0?
etb=?00? . Alors?Ax-b?2=x21et toute la droitex1= 0réalise le minimum def.Exercice 111 page 210 (Minimisation dansIR)
1. La fonctionf0est différentiable surIR, et strictement convexe.Elle admet un minimum unique surIRet sur
Ket son minimum est réalisé en¯x= 0, et on af0(¯x) = 0.2. La fonctionf1est différentiable surIR, et non convexe. La fonctionf1admet un maximum local en¯x=1
2, et on af(¯x) =116.Elle admet un minimum global non unique, réalisé en 0 et 1, et dont la valeur est 0.
3. La fonctionf2est différentiablesurIR\{0},et convexe,mais pas strictement convexe.La fonctionf2admet
quotesdbs_dbs11.pdfusesText_17[PDF] exercice corrigé modulation d'amplitude pdf
[PDF] exercice corrigé moment de force
[PDF] exercice corrigé mouvement d un projectile pdf
[PDF] exercice corrigé mouvement d'un projectile
[PDF] exercice corrigé offre et demande
[PDF] exercice corrigé onduleur monophasé
[PDF] exercice corrigé onduleur triphasé
[PDF] exercice corrigé p2 bts cgo
[PDF] exercice corrigé peps
[PDF] exercice corrigé perceptron monocouche
[PDF] exercice corrigé pic 16f877
[PDF] exercice corrigé pont tout thyristor
[PDF] exercice corrigé portique isostatique
[PDF] exercice corrigé poutre hyperstatique
