 Oscillateur harmonique Oscillateur harmonique
Oscillateur harmonique Oscillateur harmonique
13 nov. 2017 Exercice 6 : Deux ressorts à la verticale. [oral banque PT ♢♢♢]. O k1
 Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
Calculer la force qui agit sur le point commun aux deux ressorts lorsque les ressorts sont Exercices supplémentaires : Molécule diatomique. ⋆⋆. Exercice n° ...
 Oscillateur harmonique
Oscillateur harmonique
Exercice 8 : Point matériel lié à deux ressorts. Ressorts horizontaux. Un point matériel de masse m est attaché à deux ressorts hori- zontaux identiques
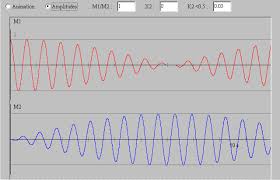 Oscillateurs couplés
Oscillateurs couplés
On considère deux points matériels de masse m1 et m2 reliés entre eux par un ressort de constante de raideur k2 et à deux points fixes par des ressorts
 TD05 – OSCILLATEUR HARMONIQUE
TD05 – OSCILLATEUR HARMONIQUE
Ce ressort est-il plus souple ou plus raide que chacun des deux ressorts dont il est formé ? Exercice 9* : Mouvement d'un électron piégé dans un puits de
 Préparation aux Olympiades Internationales de Physique
Préparation aux Olympiades Internationales de Physique
1.1 Oscillateur mécanique couplé à deux degrés de liberté . 1.3.1.2 Battements pour un système masses-ressorts (d'après QCM IPhOs CPGE 2015) . .
 Exercices de Mécanique (2ePériode) Oscillateur harmonique amorti
Exercices de Mécanique (2ePériode) Oscillateur harmonique amorti
Ex-M6.5 Oscillateurs `a deux ressorts. On considère un pendule constitué d'une tige de longueur l rigide de masse négligeable. Elle peut tourner librement
 Sans titre
Sans titre
Ce mobile est maintenu par deux ressorts à réponse linéaire dont les pour l`oscillateur électrique. 2. Leur similitude permet d`extraire certaines ...
 TD 02 (Chap. 01) – Oscillateurs harmoniques
TD 02 (Chap. 01) – Oscillateurs harmoniques
Savoir représenter et commenter le portrait de phase d'un oscillateur harmonique. II Exercices Les deux ressorts sont associés en série c'est-`a-dire mis ...
 TD CHAPITRE MK.4 : O SCILLATIONS LIBRES PARTIE 1
TD CHAPITRE MK.4 : O SCILLATIONS LIBRES PARTIE 1
-nantes.fr/sites/genevieve_tulloue/Meca/Oscillateurs/ressort.html. Exercice 13. Deux ressorts (d'après ATS 2021).
 Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
OSCILLATEUR HARMONIQUE : CORRECTIONS. Exercices prioritaires : Deux ressorts accrochés. ?. Exercice n° 1. Deux ressorts sans masse de longueurs l1 et l2 au
 Oscillateur harmonique Oscillateur harmonique
Oscillateur harmonique Oscillateur harmonique
13 nov. 2017 Exercice 2 : Une masse et deux ressorts. [??0]. Considérons un point matériel M de masse m glissant horizontalement et sans frottement ...
 Oscillateur harmonique
Oscillateur harmonique
Exercice 8 : Point matériel lié à deux ressorts. Ressorts horizontaux. Un point matériel de masse m est attaché à deux ressorts hori-.
 Oscillateur harmonique
Oscillateur harmonique
Exercice 9 : Associations de ressorts. 1. On considère deux ressorts de constantes de raideur respectives k et k et de longueurs à vide respectives l.
 TRAVAUX DIRIGÉS DE EC03.5
TRAVAUX DIRIGÉS DE EC03.5
Dans le cas 1 les deux ressorts ont la même longueur à vide l0 et la même raideur k. La Exercice 7 : Oscillateur harmonique ?
 Oscillateurs couplés
Oscillateurs couplés
On considère deux points matériels de masse m1 et m2 reliés entre eux par un ressort de constante de raideur k2 et à deux points fixes par des ressorts
 Réponse à un échelon Systèmes du second ordre
Réponse à un échelon Systèmes du second ordre
Un oscillateur harmonique mécanique est constitué d'une masse m suspendue à un ressort de raideur k et de Exercice 2 : oscillateur à deux ressorts.
 Ressorts et equations differentielles.pdf
Ressorts et equations differentielles.pdf
1 sept. 2011 II.Deux ressorts et une masse. ... On étudie ici le problème de deux oscillateurs couplés. Les trois ressorts ressort1 ressort 2.
 Sans titre
Sans titre
Ce mobile est maintenu par deux ressorts à réponse linéaire dont les extrémités sont Montrer que le système constitue un oscillateur harmonique dont on.
 SERIE DEXERCICES N° 16 : MECANIQUE : OSCILLATEURS
SERIE DEXERCICES N° 16 : MECANIQUE : OSCILLATEURS
Exercice 1. Un point matériel M de masse m = 10 g est relié à deux ressorts identiques de raideur k = 15 N.m-1
Oscillateur harmonique
Exercices
Exercice 1 : Force exercée par un ressort []
Dans chacun des cas, exprimer la force exercée par le ressort sur le solide fixé enMen fonction de la raideurk
et de la longueur naturelle?0du ressort, de la positionxouzdu pointM, de la positionxHouzHdu pointHoù
le ressort est fixé à un bâti, et du vecteur unitaire#exou#ez. Les positions sont repérées à partir du pointO. Dans le
dernier cas, exprimer les forces exercées par les deux ressorts sur chacun des pointsM1etM2, d"abscissesx1etx2.
Les deux ressorts sont supposés différents, de caractéristiquesk,?0etk?,??0.1 - xO=HM2 - xOHM3 -
x OHM 4 -zO=HM5 -z
O=HM6 -
xO=HM 1M2Exercice 2 : Une masse et deux ressorts []
Considérons un point matérielMde massemglissant horizontalement et sans frottement, repéré par son abscissex
telle que# OM=x#ex. Ce solide est relié à deux ressorts placés sur un même axe, eux-mêmes fixés enOetO?. Le
solide étudié se trouve entreOetO?. La longueurOO?est notéeL. Les ressorts ont pour raideur respectivek1etk2,
et pour longueur à vide?01et?02.1 -Faire un schéma légendé de la situation. Il va de soi qu"il sera aussi clair, complet et propre.
2 -Établir l"équation différentielle vérifiée parx(t), appelée équation du mouvement.
3 -Montrer que la position d"équilibre est donnée par
xéq=k1?01+k2(L-?02)k
1+k24 -En déduire la forme générale des solutions de l"équation du mouvement.
5 -Supposons qu"à l"instantt= 0,Mest placé enx=x0> xéqet lancé avec une vitesse initialev0vers la gauche.
Établir la loi horairex(t)et représenter son allure.6 -Supposons maintenantx0=xéqetv0= 0. Que vérifie-t-on?
Exercice 3 : Oscillateur masse-ressort vertical []L"objectif de cet exercice est de comprendre en quoi l"oscillateurverticalmontré en cours diffère de l"oscillateur
horizontalque nous avons modélisé. L"exercice propose de suivre la même démarche que celle du cours, en établissant
et résolvant l"équation différentielle régissant le mouvement, puis en contrôlant la conservation de l"énergie.
L"oscillateur de démonstration est modélisé par un ressort de longueur naturelleL0et de raideurk. Ce ressort
est attaché à une ficelle en un pointOsupposé fixe et pend verticalement. Un cylindre de massemest fixée à son
1/2Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-2018autre extrémité. La position du cylindre est repérée par sa cotez, définie le long d"un axe(Oz)orienté vers le bas
et dont l"origine est fixée au point d"attache du ressort.1 -Établir l"équation différentielle vérifiée parz(t)et l"écrire sous forme canonique. En déduire la période des
oscillations et comparer au cas horizontal.2 -Déterminer la position d"équilibrezéq. Commenter physiquement le résultat.
3 -Le cylindre est lâché sans vitesse initiale à partir d"une positionz0obtenue en étirant le ressort par rapport à la
position d"équilibre. Déterminer la loi horairez(t).4 -L"énergie potentielle du cylindre peut s"écrire sous la forme
E p(z) =12 k(z-L0)2-mgzQue représentent chacun des termes? Montrer que la solution générale obtenue traduit bien la conservation de
l"énergie mécanique du cylindre.Exercice 4 : Étude énergétique d"un oscillateur harmonique électrique []η(t)Ci(t)LuDans le circuit ci-contre, le générateur supposé idéal est brusquement éteint. On
le modélise par un échelon de courant,η(t)passant deI0à0à l"instantt= 0. On appelleEtot=EC+ELl"énergie électrique totale stockée dans le condensateur et la bobine.1 -Exprimer la dérivéedEtotdten fonction deietdidt.
2 -Justifier qualitativement queEtotest constante. En déduire l"équation différentielle vérifiée pari. Retrouver cette
équation par application des lois de Kirchoff.
3 -Établir les conditions initiales suriet sa dérivée.
4 -En déduire l"expression dei(t).
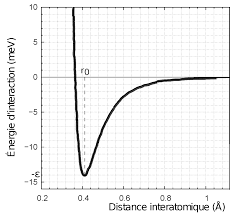
Exercice 5 : Mode de vibration d"une molécule de HCl []La fréquence de vibration de la molécule de chlorure d"hydrogène HCl est mesurée par spectroscopie comme
valantf= 8,5·1013Hz. On aborde dans cet exercice un premier modèle simple de la molécule, décrite comme un
atome d"hydrogène mobile relié à un atome de chlore fixe. L"interaction entre les deux atomes est modélisée par un
pseudo-ressort de raideurk.Données :masses molairesMH= 1,0g·mol-1etMCl= 35,5g·mol-1, nombre d"AvogadroNA= 6,0·1023mol-1.
1 -Pourquoi est-il raisonnable de supposer l"atome de chlore fixe?
2 -Calculer la raideurk.
3 -On admet que l"énergie de la molécule est égale à12
hfoùh= 6,62·10-34J·sest la constante de Planck. Calculer la vitesse maximale de l"atome d"hydrogène.4 -Calculer l"amplitude de son mouvement.Annale de concours
Exercice 6 : Deux ressorts à la verticale [oral banque PT,]O k1,?01k
2,?02m
1m21 -Si un ressort possède une raideurk, quelle est la raideur d"un demi-ressort?
2 -On considère le système ci-contre oùkiet?0isont les raideurs et longueurs à vide des ressorts.
Déterminer les allongementsΔ?1etΔ?2à l"équilibre.3 -Établir les équations différentielles vérifiées par les écartsz1etz2aux positions d"équilibre.
4 -La massem2est maintenant supposée maintenue dans sa position d"équilibre. La massem1est
alors déplacée deZdde sa position d"équilibre et lâchée sans vitesse initiale. Trouver l"équationz1(t)
régissant le mouvement dem1.5 -Quel est le rapport entre les deux premières questions de l"exercice?
2/2Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
Électronique 3 - Correction des travaux dirigésLangevin-Wallon, PTSI 2017-2018Oscillateur harmoniqueÉlectronique 3 - Correction des travaux dirigésLangevin-Wallon, PTSI 2017-2018
Oscillateur harmonique
Exercices
Exercice 1 : Force exercée par un ressort
Dans tous les cas il faut repartir de la définition, #f=-k(?-?0)#usortanten exprimant séparément?et#usortantenfonction des paramètres géométriques du problème. Attention aux signes,?est une longueur donc toujours positive.
1# f=-k(x-?0)#ex 2# f=-k(xH-x-?0)(-#ex) =k(xH-x-?0)#ex 3# f=-k(x-xH-?0)#ex 4# f=-k(-z-?0)(-#ez) =-k(z+?0)#ez 5# f=-k(z-?0)#ez6?Force exercée par le premier ressort surM1:#f=-k(x1-?0)#ex;
?Force exercée par le deuxième ressort surM1:#f=-k?(x2-x1-??0)(-#ex) =k?(x2-x1-??0)#ex;?Force exercée par le premier ressort surM2: aucune! car le premier ressort n"est pas attaché au solide enM2...
mais cela ne veut évidemment pas dire qu"il n"a pasd"influencesur le mouvement deM2; ?Force exercée par le deuxième ressort surM2:#f=-k(x2-x1-?0)#ex.Exercice 2 : Une masse et deux ressorts
1Voir figure 1.
xOO ?k1,?01k
2,?02M
LxFigure 1-Schéma de la situation.Rien n"est précisé sur la situation des ressorts (comprimés, étendus, à l"équilibre) :
il n"est donc pas possible de représenter les forces.2?Système : le solide de massem, repéré par la position du pointM;
?Référentiel : terrestre, que l"on considère en bonne approximation galiléen; ?Bilan des actions mécaniques exercées sur le système :→son poids, vertical, est supposé exactement compensé par la réaction du support sur lequel il se trouve;
→force exercée par le ressort 1 :#f1=-k1(?1-?01)#usortant,1=-k1(x-?01)#ex;→force exercée par le ressort 2 :#f2=-k2(?2-?02)#usortant,2=-k2(L-x-?02)(-#ex) =k2(L-x-?02)#ex;
→les frottements sont négligés. ?Loi de la quantité de mouvement : d #pdt=#f1+#f2avec#p=m#v=mdxdt#ex ce qui donne en projetant sur l"axex m d2xdt2=-k1(x-?01) +k2(L-x-?02).1/7Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
Correction TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-2018 Écrivons cette équation sous forme canonique, m x=k1?01+k2(L-?02)mOn reconnaît une équation différentielle d"oscillateur harmonique dont on peut identifier la pulsation propre et qu"on
écrit finalement
d2xdt2+ω20x=k1?01+k2(L-?02)m
avecω0=?k 1+k2m.3La position d"équilibre du solide est donnée par une solution particulière constante de l"équation différentielle.
Pourx=xéq=cte, elle s"écrit
0 +ω20xéq=k1?01+k2(L-?02)m
doncxéq=k1?01+k2(L-?02)mω 20 et en remplaçantmω20=k1+k2, xéq=k1?01+k2(L-?02)k
1+k2.4Les solutions de l"équation du mouvement s"écrivent toutes sous la forme d"une somme d"une solution particulière,
en l"occurencex=xéq, et d"une solution de l"équation homogène, d"où x(t) =xéq+Acos(ω0t) +Bsin(ω0t).5D"après la première condition initiale, x(0) =???? solxéq+A=????
CIx0d"oùA=x0-xéq.
Pour utiliser la seconde condition initiale, il faut connaître la vitesse, soit v x(t) =dxdt=-ω0Asin(ω0t) +ω0Bcos(ω0t). Ainsi, comme le solide est lancé vers la gauchevx(0) =-v0, donc v x(0) =???? solω0B=????
CI-v0d"oùB=v0ω
0.Finalement,
x(t) =xéq+ (x0-xéq)cos(ω0t) +v0ω0sin(ω0t).6Voir figure 2. Points importants du tracé : oscillations symétriques par rapport à la position d"équilibrexéq, qui
restent bornées entre 0 etL. Les conditions initiales doivent apparaître clairement :x(0)> xéqet la pente initiale
doit être négative car le solide est lancé vers la gauche.tx(t)L xéqFigure 2-Allure dex(t).
7Avec ces nouvelles conditions initiales, la résolution reste formellement la même mais donne
A=B= 0soit?t, x(t) =xéq
On vérifie ainsi quexéqest bien une position d"équilibre du système.2/7Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
Correction TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-2018Exercice 3 : Oscillateur masse-ressort vertical
z0 z(t)OM1?Système : le cylindre de massem;
?Référentiel : celui de la classe, identique au référentiel terrestre, considéré galiléen;
?Bilan des actions mécaniques : →Poids :#P=m#g=mg#ez; →Force de rappel du ressort : #Fr=-k(L-L0)#usortant=-k(z-L0)#ez ?Loi de la quantité de mouvement :d#pdt=#P+#Fr avec #p=mvz#ezdoncd#pdt=mdvzdt#ez=md2zdt2#ez. Ainsi, en remplaçant les expressions des forces, m d2zdt2#ez=mg#ez-k(z-L0)#ez. Il reste alors à projeter l"équation différentielle, m d2zdt2=mg-k(z-L0), et à l"écrire sous forme canonique, d2zdt2+ω20z=g+kL0m
avecω0=?k m.La pulsation propre a la même expression dans le cas vertical que dans le cas horizontal,la période des oscillations
est donc la même dans les deux cas.2Les positions d"équilibre sont les solutions particulières constantes de l"équation du mouvement. Ici,zéqest tel
que0 +ω20zéq=g+kL0m
soitzéq=gω20+kL0mω
20d"oùzéq=mgk
+L0.On remarque quezéq> L0, ce qui est raisonnable car à l"équilibre le ressort doit compenser le poids du cylindre. En
outre, on note quezéqest d"autant plus grand (donc la position d"équilibre d"autant plus basse) quemest élevée et
d"autant moins que le ressort est raide, ce qui est là aussi raisonnable.On peut noter que la position d"équilibre estexactementdonnée par la longueur du ressort pour laquelle
le poids et la force de rappel se compensent,P+#Fr=#0soitmg-k(zéq-L0) = 0donczéq=mgk
+L0.3Commez=zéqest solution particulière, les solutions de l"équation différentielle s"écrivent toutes sous la forme
z(t) =zéq+Acos(ω0t) +Bsin(ω0t). Les constantesAetBse trouvent à partir des conditions initiales, z(0) =???? CIz0=????
solzéq+A+ 0d"oùA=z0-zéq.
Pour exploiter la deuxième condition initiale, il faut obtenir la vitesse par dérivation, v z=dzdt=-ω0Asin(ω0t) +ω0Bcos(ω0t) et ainsi v z(0) =????CI0 =????
sol0 +Bd"oùB= 0.Finalement,
z(t) =zéq+ (z0-zéq)cos(ω0t).3/7Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
Correction TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-20184Le premier terme en
12 k(z-L0)2est l"énergie potentielle élastiqueque le ressort est à même de fournir au solide. Le second terme en-mgzest l"énergie potentielle de pesanteurdu solide. Commençons par calculer l"énergie potentielle élastique, E pe=12 k[zéq+ (z0-zéq)cos(ω0t)-L0]2 12 k?mgk + (z0-zéq)cos(ω0t)? 2 12 k? ?mgk2+ 2mgk
(z0-zéq)cos(ω0t) + (z0-zéq)2cos2(ω0t)? m2g22k+mg(z0-zéq)cos(ω0t) +12 k(z0-zéq)2cos2(ω0t).L"énergie potentielle de pesanteur s"écrit
E pp=-mgzéq-mg(z0-zéq)cos(ω0t). Enfin, l"expression de la vitesse calculé précédemment permet d"obtenir E c=12 mω20(z0-zéq)2sin2(ω0t). Finalement, en simplifiant déjà le terme encos(ω0t), E m=m2g22k+12 k(z0-zéq)2cos2(ω0t)-mgzéq+12 mω20(z0-zéq)2sin2(ω0t)Commeω0=?k/malorsmω20=k, ce qui permet de factoriser et d"utilisercos2(ω0t) + sin2(ω0t) = 1. Ainsi,
E m=m2g22k+12 k(z0-zéq)2-mgzéqOn montre bien ici que l"énergie mécanique est constante, et on note que la constante dépend des conditions initiales
par l"intermédiaire dez0. Pour simplifier l"expression, on peut remplacerzéqpar son expression et développer ... mais
c"est lourd, lourd, très lourd. Il est plus astucieux de remarquer que l"énergie mécanique garde constamment sa valeur
intiale. Comme à l"instant initialvz= 0, alors E m=12k(z0-L0)2-mgz0.Nous reverrons tous ces points de façon plus systématique dans le cours de mécanique.
Exercice 4 : Étude énergétique d"un oscillateur harmonique électrique1Exprimons l"énergie totale,
E tot=12Cu2+12
Li2.Ainsi, en dérivant,dEtotdt=12
C×2ududt+12
L×2ididt.
Comme seule l"intensité doit apparaître dans le résultat, on remplaceuavec la loi de comportement de la bobine,
soit dEtotdt=12C×2Ldidtddt?
Ldidt?
+12L×2ididt
=L2Cdidtd2idt2+Lididt
dEtotdt=Ldidt?LCd2idt2+i?2Le circuit ne compte qu"une bobine et un condensateur, qui stockent de l"énergie mais n"en dissipent pas, et il
n"y a en particulier aucune résistance. L"énergie électrique dans le circuit est donc constante. On en déduit qu"à tout
instant, dEtotdt= 0soitLdidt?LCd2idt2+i?
= 0.4/7Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr
Correction TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-2018Le terme en facteurLdi/dtest la tension aux bornes de la bobine, qui n"est pas constamment nulle. C"est donc le
terme dans la parenthèse qui est nul, soit LC d2idt2+i= 0soitd2idt2+ω20i= 0,en posantω0= 1/⎷LCla pulsation propre du circuit.η(t)Ci Ci(t)Lu3Retrouvons cette équation par les lois de Kirchoff. D"après la loi des noeuds, iC+i= 0doncCdudt+i= 0
Comme la bobine et le condensateur sont montés en parallèle, ils sont soumis à la même tensionu, et donc d"après
la loi de comportement de la bobine, LC d2idt2+i= 0.4À l"instantt= 0-, le circuit est encore en régime permanent avecη=I0. La bobine est donc équivalente à un
fil et le condensateur à un interrupteur ouvert. On en déduit que i(0-) =I0etu(0-) = 0.Commeidoit être continu (bobine), alors
i(0+) =i(0-) =I0.Par ailleurs, comme le condensateur est monté en parallèle de la bobine alorsuest aussi la tension aux bornes du
condensateur et doit donc aussi être continue, donc u(0+) =u(0-) = 0.D"après la loi de comportement de la bobine,
Ldidt(0+) =u(0+) = 0soitdidt(0+) = 0.5Forme générale des solutions :l"équation est homogène, il n"y a donc pas de solution particulière à prendre en
compte (une autre façon de le dire est que la solution particulière est nulle). On en déduit que les solutions s"écrivent
toutes sous la forme i(t) =Acos(ω0t) +Bsin(ω0t).Détermination des constantesAetB:d"une part,
i(0-) =i(0+) =???? solA=???? CII0d"oùA=I0,
et d"autre part, comme didt=-ω0Asin(ω0t) +ω0Bcos(ω0t) alorsdidt(0+) =???? solω0B=????
CI0d"oùB= 0.
Conclusion :
i(t) =I0cos(ω0t).Exercice 5 : Mode de vibration d"une molécule de HCl1Au vu des masses molaires, l"atome de chlore est beaucoup plus lourd que l"atome d"hydrogène, et doncbeaucoup
plus difficile à mettre en mouvement. Il est donc raisonnable de supposer que seul l"atome d"hydrogène est en
mouvement.2Le système est équivalent à un mobile (l"atome H) relié à un support fixe (l"atome Cl) par un ressort, c"est-à-dire
un oscillateur harmonique. Sa fréquence proprefest alors reliée à la massemH=MH/NAde l"atome H et à la
raideurkdu ressort par f=12π?k mH=12π?kNAM
Hd"oùk=4π2f2MHN
A= 4,7·102N·m-15/7Étienne Thibierge, 13 novembre 2017,www.etienne-thibierge.fr Correction TD E3 : Oscillateur harmonique Langevin-Wallon, PTSI 2017-2018Attention pour calculer la valeur numérique à bien convertir la masse molaire en kg·mol-1!3La vitesse de l"atome d"hydrogène est maximale lorsque celui-ci passe par sa position moyenne, correspondant
à la longueur naturelle du pseudo-ressort car aucune autre force n"est envisagée. À ces points particuliers, l"énergie
mécanique de l"atome d"hydrogène est sous forme seulement d"énergie cinétique,Em=Ec=mHv2max/2. Ainsi,
12 hf=12 mHv2maxd"oùvmax=?hfNAMH= 5,8·103m·s-14La position de l"atome est égale à l"amplitudeXmaxde son mouvement aux points de rebroussement. À ces
points particuliers, l"énergie mécaniqueEmde l"atome d"hydrogène est sous forme seulement d"énergie potentielle,
E m=Ep=kX2max/2. Ainsi, 12 hf=12 kX2max=124π2f2MHN
AX2max
d"où Xmax=?hNA4π2f MH= 1,1·10-11m = 11pm.Pour comparaison, la longueur de la liaison H-Cl est tabulée à 127pm. Ce modèle (simpliste!) indique
qu"elle varie de près de 10% sous l"effet de la vibration.Pour aller plus vite dans le calcul, on aurait aussi pu utiliser le fait qu"amplitude du mouvement et
vitesse maximale sont reliées parvmax=ω0XmaxAnnale de concours Exercice 6 : Deux ressorts à la verticale [oral banque PT] O opérateurz? 02 +Δ?2 02 +Δ?21Question bien compliquée pour commencer! Considérons un ressort complet fixé àune de ses extrémités et une massemtrès faible fixée au milieu. Un opérateur tire sur le
ressort en lui donnant un allongementΔ?. La force exercée par le ressort sur l"opérateur vaut#F= +kΔ?#uz Comme la force exercée par le ressort est opposée aux deux extrémités1, on en déduit
quotesdbs_dbs17.pdfusesText_23[PDF] exercice oscillateur harmonique non amorti
[PDF] exercice p a inter b
[PDF] exercice papier crayon remédiation cognitive
[PDF] exercice parallélogramme 5eme a imprimer
[PDF] exercice parallélogramme 5eme corrigé
[PDF] exercice parallélogramme 5eme pdf
[PDF] exercice parallélogramme particulier 5eme
[PDF] exercice pareto maintenance
[PDF] exercice partie double
[PDF] exercice pendule simple terminale s
[PDF] exercice peps cump
[PDF] exercice perimetre cercle 6eme
[PDF] exercice perimetre cercle 6eme a imprimer
[PDF] exercice perimetre d'un cercle 6eme
