 Cours sections planes de solides
Cours sections planes de solides
cône et A' le point de C' appartenant au segment [SA]. Le coefficient de réduction k est : k = = = VII) Section plane d'une pyramide : 1) Définition : La ...
 Code : Thème : Géométrie de lespace LECON 14 : PYRAMIDES ET
Code : Thème : Géométrie de lespace LECON 14 : PYRAMIDES ET
= 100 3. III. Sections planes. 1. Section d'une pyramide régulière par un C'est la section du cône par le plan (P). On obtient un petit cône de sommet S ...
 SECTIONS PLANES DUN PAVE DROIT DUN CYLINDRE
SECTIONS PLANES DUN PAVE DROIT DUN CYLINDRE
http://college-bourbon.ac-reunion.fr/wp-content/uploads/sites/10/2020/04/COURS_Sections_Solides-autres-que-boules.pdf
 Cours sections planes de solides
Cours sections planes de solides
cône et A' le point de C' appartenant au segment [SA]. Le coefficient de réduction k est : k = = = VII) Section plane d'une pyramide : 1) Définition : La ...
 SECTIONS PLANES AGRANDISSEMENT
SECTIONS PLANES AGRANDISSEMENT
http://luxpierre.free.fr/documents/cours/3/sections_planes.pdf
 Cours sections planes de solides _prof_ bis
Cours sections planes de solides _prof_ bis
i) Quelle est la section d'une pyramide par un plan parallèle à sa base ? j) Quelle est la section d'un cône de révolution par un plan parallèle à sa base ?
 Cours sections planes de solides
Cours sections planes de solides
VI) Section plane d'un cône de révolution. 1) Définition : La section d'un VII) Section plane d'une pyramide. 1) Définition : La section d'une pyramide par ...
 A square pyramid 50 mm base side and axis 90 mm long is resting
A square pyramid 50 mm base side and axis 90 mm long is resting
The pyramid is cut by a section plane inclined at 45° to HP and Draw the projections of the cone showing sectional views and the true shape of the section.
 Untitled
Untitled
If the base is a polygonal region then the cone is usually called a pyramid. General Pyramids and Cones and Their Cross-Sections. This work is derived ...
 Untitled
Untitled
Lesson 7: General Pyramids and Cones and Their Cross-Sections. Classwork. Opening Exercise. Cylinder / cone/ Pyramid /or Prism. Group the following images by
 Cours sections planes de solides
Cours sections planes de solides
j) Quelle est la section d'un cône de révolution par un plan parallèle à sa VII) Section plane d'une pyramide : 1) Définition :.
 CH 14 bis : Sections planes
CH 14 bis : Sections planes
SECTIONS PLANES D'UNE PYRAMIDE OU D'UN CONE DE REVOLUTION. PROPRIETES : ? La section d'une pyramide par un plan parallèle à sa base est une réduction du
 Géométrie dans lespace
Géométrie dans lespace
Section plane d'un cône de révolution : La section plane d'une pyramide par un plan parallèle à sa base est une réduction de sa base. La nouvelle pyramide
 Chapitre 5 : agrandissement réduction ; sections de solides
Chapitre 5 : agrandissement réduction ; sections de solides
6 jan. 2011 On obtient une section qui a la même forme que les bases : un cercle. ... 4/ Pyramide et cône de révolution (4ème).
 3ème : Chapitre17 Sections de solides – Agrandissements réductions
3ème : Chapitre17 Sections de solides – Agrandissements réductions
La section d'un cylindre de révolution par un plan parallèle à l'axe est un rectangle. 3. Section d'une pyramide ou d'un cône par un plan.
 SECTIONS PLANES (P)
SECTIONS PLANES (P)
Rq: Le centre du disque "réduit" appartient à la hauteur du cône de révolution. III. Section d'une pyramide: La section d'une pyramide par un plan parallèle à
 Cours sections planes de solides
Cours sections planes de solides
i) Quelle est la section d'une pyramide par un plan parallèle à sa base ? j) Quelle est la section d'un cône de révolution par un plan parallèle à sa.
 CHAPITRE XIII : SECTIONS PLANES I. Parallélépipède rectangle
CHAPITRE XIII : SECTIONS PLANES I. Parallélépipède rectangle
CHAPITRE XIII : SECTIONS PLANES. I. Parallélépipède rectangle. • La section d'un pavé droit par un plan Cônes de révolution. La section d'un cône de ...
 CHAPITRE 10 : SECTION PLANE DE SOLIDES
CHAPITRE 10 : SECTION PLANE DE SOLIDES
IV. PYRAMIDE ET CONE DE REVOLUTION. La section d'une pyramide ou d'un cône de révolution par un plan parallèle à la base est une réduction de la base.
 Télécharger en PDF les sections de solides : volumes réduction et
Télécharger en PDF les sections de solides : volumes réduction et
Sections planes de solides La section d'une pyramide par un plan (P) parallèle à la base est un polygone ... Section d'un cône de révolution par un plan.
 Sections planes : cône et pyramide - MAXICOURS
Sections planes : cône et pyramide - MAXICOURS
Plane sections of a cone 5 The intersection of any cone and a plane is always an ellipse a parabola or an hyperbola It is simple to parametrize it and not too dif?cult to tell exactly what its location and dimensions are (when the cone is right-circular) Namely we can essentially parametrize it as we do a circle
 1 PYRAMIDE ET CÔNE - maths et tiques
1 PYRAMIDE ET CÔNE - maths et tiques
1) Exemple d’introduction : Une pyramide réduite C Les faces CBA et CBD de la pyramide sont des triangles rectangles en B et la base DBA est un triangle rectangle et isocèle en B CB = 6 cm et AB = 4 cm 1) Calculer : • L’aire du triangle DBA ; • Le volume de la pyramide CDAB
 Les sections planes (EG3) - Mathez ça
Les sections planes (EG3) - Mathez ça
On appelle section d'un solide par un plan l'intersection de ce solide avec ce plan Grâce aux vidéos suivantes vous allez visualiser la section d'un cube d'un pavé droit d'un cylindre d'un cône d'une pyramide et d'une sphère par un plan https://www youtube com/watch?v=v-V3z3fO9d4 : cette vidéo est un peu
 3ème : Chapitre17 Sections de solides – Agrandissements
3ème : Chapitre17 Sections de solides – Agrandissements
La section d'un pavé droit par un plan P parallèle à une arête est un rectangle 2 Section d'un cylindre de révolution par un plan La section d'un cylindre de révolution de rayon R par un plan perpendiculaire à l'axe est un cercle de rayon R et dont le centre appartient à cet axe
 Searches related to sections planes cône et pyramide PDF
Searches related to sections planes cône et pyramide PDF
Pyramide et cône: Propriété : La section plane d’une pyramide ou d’un cône par un plan parallèle à sa base est une figure de même nature que celle de la base La base de ce cône est un disque de centre O et de rayon OA La section est donc un disque également (de centre I et de rayon IJ) La base de cette pyramide est la carré ABCD
Comment calculer la section plane d’un cône de révolution par un plan parallèle à sa base ?
La section plane d’un cône de révolution par un plan parallèle à sa base est un disque. Ce disque est une réduction du disque de base. Soit le cône de révolution d’axe ( SO) et de rayon de base OP (voir figure ci-contre). P est un plan parallèle à la base. La section obtenue alors est un disque de centre A et de rayon AB.
Qu'est-ce que la section d'une pyramide par un plan parallèle à la base ?
La section d'une pyramide par un plan parallèle à la base est un polygone de même forme que la base : ses côtés sont parallèles à ceux de la base. La section d'un cône de révolution par un plan parallèle à la base est un cercle dont le centre appartient à la hauteur du cône. doc A.Garland page2/2Collège Jules Ferry de Neuves Maisons 4.
Comment calculer la section plane d’une pyramide par un plan parallèle à sa base ?
La section plane d’une pyramide par un plan parallèle à sa base est un polygone. Ce polygone est une réduction du polygone de base. SABCD est une pyramide régulière à base carrée ABCD. P est un plan parallèle à la base. La section obtenue est ainsi un carré, réduction du carré ABCD. Le rapport de réduction est .
Comment construire une pyramide?
Construire le patron de la pyramide GABC inscrite dans le cube ABCDEFGH. On commence par tracer par exemple la base de la pyramide : le triangle ABC rectangle et isocèle en B tel que AB = BC = 6 cm. On trace ensuite la face de droite : le triangle BCG rectangle et isocèle en C tel que CG = 6 cm.
PYRAMIDE ET CÔNE
I. La pyramide
1) Vocabulaire
Définition :
Une pyramide est un solide formé d'un
polygone " surmonté » d'un sommet.S : le sommet
En vert : la base, un polygone
En rouge : les arêtes latérales
En bleu : la hauteur Pyramide du Louvre - Paris2) Une pyramide particulière : le tétraèdre
Vient du grec tetra (= 4) et edros (= base)
Euclide a prouvé qu'il existe seulement 5 polyèdres réguliers (toutes les faces sont des polygones réguliers) :
l'icosaèdre, le dodécaèdre, le tétraèdre, le cube, l'octaèdre. Ce sont les polyèdres de Platon qui symbolisaient
selon lui : l'Eau, l'Univers, le Feu, la Terre et l'Air.La base est un triangle
2 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr3) Patron
Méthode : Construire un patron d'une pyramide
Vidéo https://youtu.be/GXkxA__A44A
Construire le patron de la pyramide GABC inscrite
dans le cube ABCDEFGH. On commence par tracer par exemple la base de la pyramide : le triangle ABC rectangle et isocèle en B tel que AB = BC = 6 cm.On trace ensuite la face de droite :
le triangle BCG rectangle et isocèle en C tel queCG = 6 cm.
On trace ensuite la face arrière :
le triangle ACG rectangle en C tel queCG = 6 cm.
On finit en traçant la face de devant : le triangle ABG. Pour cela, on reporte au compas les longueurs AG et BG déjà construites sur les autres triangles.A E F D C B G H 6cm
3 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frII. Le cône de révolution
1) Vocabulaire
Définition :
Un cône (ou cône de révolution) est un solide obtenu en faisant tourner un triangle rectangle
autour d'un des côtés de l'angle droit. En grec " kônos » signifiait une pomme de pinS : le sommet
En vert : la base, un disque
En rouge : les génératrices
En bleu : la hauteur
B A C G G 6 cm G S
4 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr2) Patron :
Méthode : Construire un patron d'un cône
Vidéo https://youtu.be/hepr9p3Svbw
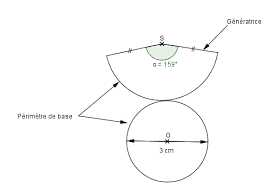
Construire le patron du cône ci-contre.
On commence par faire un patron à main levée. - Périmètre de la base = 2������=2���×3=6���Or, le périmètre de la base est égal au périmètre de l'arc ������ car ils se touchent.
Donc :
Périmètre de l'arc ������ =6���
- Périmètre du disque de centre S et de rayon 5 cm = 2×���×5=10���. Dans un cercle, la longueur de l'arc est proportionnelle à la mesure de l'angle au centre qui le définit.Angle au centre 360
Longueur de l'arc 10��� 6���
On construit ainsi le patron en vraie grandeur :
O S B A 5cm 3cm 216°
5 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frIII. Volumes
1) Rappels : formules d'aires
6 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr2) Formules de volumes
Un premier exemple simple :
Vidéo https://youtu.be/RzIJ5Fq2fiU
Méthode : Calculer le volume d'une pyramide
Vidéo https://youtu.be/KKon_cIVd9k
AB = 4 cm et CH = 5 cm.
La hauteur de la pyramide est de 3,5 cm
Calculer son volume arrondi au centième de cm
3Calcul de l'aire de la base :
La base est un triangle de hauteur CH = 5 cm.
S 3,5 cm H C B A
7 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr A = = 10 cm 2Calcul du volume de la pyramide :
La pyramide a pour hauteur ��� = 3,5 cm.
V = cm 3» 11,67 cm
3Calcul du volume d'un cône :
Vidéo https://youtu.be/kMssaNRPXz8
IV. Agrandissement et réduction
1) Exemple d'introduction : Une pyramide réduite
Les faces CBA et CBD de la pyramide sont des triangles rectangles en B et la base DBA est un triangle rectangle et isocèle en B.CB = 6 cm et AB = 4 cm.
1) Calculer :
• L'aire du triangle DBA ; • Le volume de la pyramide CDAB.2) On coupe la pyramide par un plan parallèle à la base passant par le
point E tel que CE = 3 cm. La pyramide CGFE est une réduction de la pyramide CDAB.Calculer :
• Le coefficient de réduction ; • L'aire du triangle GEF ; • Le volume de la pyramide CGFE.1) • A
DBA = B x h : 2 = 4 x 4 : 2 = 8 cm 2 • V CABD = A DBA x H : 3 = 8 x 6 : 3 = 16 cm 32) •
0 = 0,50,5 est le coefficient de réduction. ➜ Les longueurs sont multipliées par 0,5.
• (EF = GE= 0,5 x 4 = 2 cm) A GEF = B x h : 2 = 2 x 2 : 2 = 2 cm 2Compléter : A
GEF = ? x A DBA2 = ? x 8
? = 2 : 8 = 0,25 (= 0,5 2 A GEF = 0,5 2 x A DBA ➜ Les aires sont multipliées par 0,5 2C 4cm 6cm E G F B A D
8 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr • V CEFG = A GEF x H : 3 = 2 x 3 : 3 = 2 cm 3Compléter : V
CEFG = ? x V CABD2 = ? x 16
? = 2 : 16 = 0,125 (= 0,5 3 V CEFG = 0,5 3 x V CABD ➜ Les volumes sont multipliés par 0,5 32) Propriétés
Propriétés :
Pour un agrandissement ou une réduction de rapport k, -les longueurs sont multipliées par k, -les aires sont multipliées par k 2 -les volumes sont multipliés par k 3 Remarque : Dans la pratique, on applique directement la propriété.3) Application
Méthode : Appliquer un agrandissement ou une réductionVidéo https://youtu.be/YBwMKghrSOE
Le récipient représenté ci-contre a une forme conique et a pour dimensions : OM = 6 cm et SO = 12 cm.1) Calculer, en cm
3 , le volume de ce récipient. Donner la valeur exacte puis la valeur arrondie au dixième de cm 32) On remplit d'eau le récipient jusqu'au point O' tel que SO' = 4,5 cm.
Le cône formé par l'eau est une réduction du cône initial.Calculer le coefficient de réduction.
3) Déduire une valeur approchée du volume d'eau.
1) Aire de la base du récipient :
Il s'agit d'un disque de rayon OM = 6 cm, donc : A = pR 2 = p x 6 2 = 36pVolume du récipient :
Il s'agit d'un cône de hauteur SO = 12 cm, donc : 336���×12
3 =144��������� =452,4������2) Coefficient de réduction :
Le coefficient de réduction est le rapport de deux longueurs qui se correspondent sur les deux solides. On prend ici les hauteurs SO et SO' des deux solides. 4,5 12 =0,3753) Pour une réduction de rapport k =0,375, les volumes sont multipliés par k
3 =0,375 3 Ainsi, le volume du petit cône correspondant à l'eau dans le récipient est égal à : =452,4×0,375 =23,9������ 9 Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frV. Repérage dans l'espace
1) Repère de l'espace
Un parallélépipède peut définir un repère de l'espace. Il faut choisir une origine (ici le point A) et trois axes gradués définis à partir des dimensions du parallélépipède : abscisse - ordonnée - altitude Méthode : Se repérer sur le parallélépipède rectangleVidéo https://youtu.be/OTUHNsf1Gek
On donne le repère de l'espace représenté ci-dessous défini à partir du parallélépipède
ABCDEFGH.
Donner l'abscisse, l'ordonnée et l'altitude des sommets du parallélépipède et du milieu K du
segment [FG].Pour chaque point, on note dans l'ordre entre parenthèses l'abscisse, l'ordonnée et l'altitude.
A(0 ; 0 ; 0) E(0 ; 0 ; 4) K(3,5 ; 5 ; 4)
B(0 ; 5 ; 0) F(0 ; 5 ; 4)
C(7 ; 5 ; 0) G(7 ; 5 ; 4)
D(7 ; 0 ; 0) H(7 ; 0 ; 4)
Hors du cadre de la classe, aucune reproduction, même partielle, autres que celles prévues à l'article L 122-5 du code de la propriété intellectuelle, ne peut être faite de ce site sans l'autorisation expresse de l'auteur. www.maths-et-tiques.fr/index.php/mentions-legales
quotesdbs_dbs4.pdfusesText_8[PDF] Sédimentation et apparition de la vie sur Terre
[PDF] Sens de variation de u + lambda, de lamba.u, racine de u et de 1/u
[PDF] Sens de variation d’une suite
[PDF] Séparation et identification des espèces chimiques
[PDF] Séparer les constituants d’un mélange hétérogène
[PDF] Ser + nom
[PDF] Ser et Estar
[PDF] Seven days in a week
[PDF] Shakespeare
[PDF] Si c’est un homme : la structure de l’?uvre
[PDF] Si c’est un homme : l’auteur
[PDF] Si c’est un homme : l’espace et le temps
[PDF] Si c’est un homme : problématiques essentielles
[PDF] Signe du trinôme du second degré
