Ordre. Inéquations du 1er degré. Valeur absolue
Résoudre une inéquation dans R c'est déterminer l'intervalle ou l'union d'intervalles des valeurs de l'inconnue qui vérifient celle-ci. 2.2 Règles de
Équation et inéquation avec des valeurs absolues
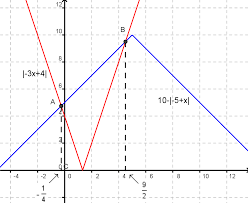
On détermine les valeurs frontières de chaque valeur absolue : −3x + 4 = 0 soit x = 4. 3. −5 + x = 0 soit x = 5. On remplit un tableau de forme :.
TD NO 1 1 Équations – Inéquations – Valeur absolue 2 Généralités
ÉQUATIONS – INÉQUATIONS – FONCTIONS. 1 Équations – Inéquations – Valeur absolue. £. ¢. ¡. 1 Résoudre les inéquations suivantes d'inconnue réelle x : a) 1−x2
Partie 1 : Intervalles de ℝ
- La valeur absolue de 5 est égale à 5 et on note
Valeur absolue 1 Définition et règles de clalcul 2 Règles de calcul
inéquations avec valeurs absolues. La valeur absolue est une "écriture condensée". Dans les exercices en général
ÉQUATIONS INÉQUATIONS
c) Tester l'égalité pour différentes valeurs de x dans le but de trouver le nombre de moutons que M. Bèhè possédait au printemps. Page 2. 2. Yvan Monka –
Résolution des équations et inéquations avec valeur absolue
2) Résolution des inéquations avec valeur absolue. L'inéquation
Exercices sur les inéquations du 1er degré et les valeurs absolue
Exercices sur les inéquations du 1er degré et les valeurs absolue. 2. 28 2x − x − 1. 5. ⩾. 1. 4. − x. 29. 1. 3 x +. 1. 4. > x +. 1. 2. 30 2(x − 1) − 3(x +
Equation et inequation avec valeur absolue pdf
Equation et inequation avec valeur absolue pdf. La valeur absolue d'un nombre Graphiquement on a : Équation et inéquation avec des valeurs absolues 1 ...
Ordre. Inéquations du 1er degré. Valeur absolue
TABLE DES MATIÈRES. 1. Ordre. Inéquations du 1er degré. Valeur absolue. Paul Milan. LMA Seconde le 15 novembre 2012. Table des matières. 1 Intervalle dans R.
Équation et inéquation avec des valeurs absolues
1 Équation. Résoudre dans R l'équation suivante :
Chapitre 1 Calculs algébriques élémentaires
utilisant la définition de la valeur absolue. Cela conduit donc à résoudre l'équation ou l'inéquation sur différents intervalles (les valeurs absolues
1 S Exercices sur la valeur absolue (1)
8 Résolution d'inéquations avec valeurs absolues. Résolvons dans l'inéquation
1 S Exercices sur la valeur absolue (1)
8 Résolution d'inéquations avec valeurs absolues. Résolvons dans l'inéquation
Présentation PowerPoint
Résolution d'une inéquation comportant la valeur absolue. VALEUR ABSOLUE D'UN. NOMBRE ET FONCTION. VALEUR ABSOLUE. ? Fonction valeur absolue et son graphe.
Première S Exercices valeur absolue 2010-2011 1 Exercice 1
Résoudre dans Y les inéquations suivantes : Exercices valeurs absolue ... On détermine l'ensemble I des solutions de la première inéquation et ...
NOMBRES RÉELS (Partie 2)
Résoudre une inéquation c'est trouver toutes les valeurs de x qui vérifient Définition : La valeur absolue d'un nombre A est égal au nombre A si A est ...
1ère S Cours sur la valeur absolue _3_
II. Notation de la valeur absolue d'un réel. III. Résolutions d'équations et d'inéquations avec des valeurs absolues en utilisant la définition.
CHAPITRE 3 ÉQUATIONS ET INÉQUATIONS 3-1 ÉQUATIONS ET
La valeur absolue d'un nombre x est la distance sur la droite réelle entre l'origine Les équations et inéquations comportants des valeurs absolues sont ...
Ordre Inéquations du 1er degré Valeur absolue
2 Inéquation du 1er degré dans R 2 1 Dé?nition Dé?nition 4 On appelle inéquation à une inconnue une inégalité qui n’est véri?ée que pour certaines valeurs de cette inconnue dont on se propose de déterminer les valeurs s Des inéquations du 1er degré : x ?3 0 Des inéquations du 2nd degré :
NOMBRE ET FONCTION VALEUR ABSOLUE - HEC Montréal
Résolution inéquation avec valeur absolue d’un nombre Exemple 3 Trouver l’ensemble des valeurs réelles vérifiant x 41 6 À mémoriser x d4 1
Équation et inéquation avec des valeurs absolues
Équation et inéquation avec des valeurs absolues 1 Équation Résoudre dans R l’équation suivante : j3x +4j+j5+ xj= 10 (E 1) 2 On détermine les valeurs frontières de chaque valeur absolue : 3x +4 = 0 soit x = 4 3 5+ x = 0 soit x = 5 2 On remplit un tableau de forme : x 1 4 3 5 +1 j3x +4j 3x +4 0 3x 4 11 3x 4 j5+ xj 5 x 11 3 5 x 0 5+ x (E
Searches related to inéquation valeur absolue PDF
Chapitre 4 : Intervalles - Inéquations – Valeur absolue I - Ensemble ? des réels et intervalles Définitions : L'ensemble des abscisses des point d'une droite graduée est appelé l'ensemble des nombres réels On le note ? Soient a et b sont deux réels tels que a < b
Comment résoudre une inéquation contenant une valeur absolue ?
Pour résoudre une inéquation contenant une valeur absolue, il est utile de tracer un graphique afin de déterminer l'ensemble-solution. 1. Remplacer le symbole d'inégalité par le symbole d'égalité. 2. Isoler la valeur absolue. 3. Appliquer la définition de la valeur absolue tout en indiquant les restrictions.
Comment résoudre une équation contenant une valeur absolue ?
Pour résoudre une équation contenant une valeur absolue, il faut se référer à la définition de la valeur absolue. 1. Isoler la valeur absolue d'un côté de l'égalité. 2. Appliquer la définition de la valeur absolue. 3. Résoudre les deux équations obtenues précédemment. 4. Vérifier les solutions. 5. Donner l'ensemble-solution.
Quelle est la valeur absolue de a ?
Définition : Soient a et b, deux nombres réels. 1) La distance entre 2 et 6 est égale à 4. 2) La distance entre 5 et -4 est égale à 9. Définition : Soit a un nombre réel, on appelle valeur absolue de a la distance à 0 de a.
Qu'est-ce que les inégalités de valeur absolue ?
Les inégalités de valeur absolue sont des inégalités dans lesquelles il y a un ou plusieurs valeur absolue . Rappelons qu'une inégalité est presque comme une équation, mais au lieu du signe "=", nous avons "?" ou "?". Cette différence fait que l'ensemble de solutions est généralement une région, comme pour la plupart des inégalités.
Chapitre 1
Calculs algébriques élémentaires
1. La valeur absolue
Soitxun nombre réel, on définit la valeur absolue dexpar :?|x|=xsix?0 |x|=-xsix<0On constate, avec cette définition, que|x|est nécessairement un nombre positif ou nul. En fait,|x|
représente la distance du point M d"abscissexà l"origine sur la droite graduée des réels.
Rappel de cours.
Voici à présent quelques techniques usuelles permettant de résoudre des équations ou inéquations compor-
tant des valeurs absolues.Pour résoudre une équation (ou inéquation) avec des valeurs absolues, on peut essayer de se ra-
mener à l"une des situations suivantes (a?R1.|x|=a?x=±a,
2.|x|?a?x?[-a;a],
3.|x|?a?x?]-∞;-a]?[a;+∞[.
Application : exercices 1 et 2.
Méthode 1(Équations ou inéquations de référence).Remarque.Les résultats énoncés dans la méthode précédente se retrouvent à l"aide d"un dessin.
Pour tout réelx,ona|x|
2 =x 2 . C"est donc un moyen de faire "sauter" une valeur absolue ce qui estpeut être intéressant si les expressions générées par la mise au carré restent "raisonnables".
Application : exercice 3.
Méthode 2(Mise au carré).
Remarque.On retiendra également que pour toutxréel,? x 2 =|x|. 5 51. Calculs algébriques élémentaires
Lorsqu"on ne peut pas se ramener aux configurations ci-dessus, on peut alors envisager différentscas en étudiant au préalable le signe des quantités intervenant dans les valeurs absolues et en
utilisant la définition de la valeur absolue. Cela conduit donc à résoudre l"équation ou l"inéquation
sur différents intervalles (les valeurs absolues auront disparu).Application : exercice 4.
Méthode 3(Examiner le signe des quantités).
Résoudre dansR:
1.|x-2|=4,
2.|x+5|=-3.
Exercice 1(?).
Solution.
1. On a les équivalences suivantes :
|x-2|=4?x-2=-4oux-2=4 ?x=-2oux=6.DoncS={-2 ; 6}.
2. Une valeur absolue ne peut pas être strictement négative, doncS=?.
Résoudre dansR,
1.|x+3|?2,
2.|x-1|>5.
Exercice 2(??).
Solution.
1. On a les équivalences suivantes :
|x+3|?2?-2?x+3?2 ?-5?x?-1.DoncS=[-5 ; 1].
2. On a les équivalences suivantes :
|x-1|>5?x-1<-5oux-1>5 ?x<-4oux>6.DoncS=]-∞;-4[?]6 ;+∞[.
Soitxetydeux réels. Démontrer que|x+y|?|x|+|y|. Cette inégalité est appelée "inégalité triangulaire".Exercice 3(???).
6 61. Calculs algébriques élémentaires
Solution.
On a les équivalences suivantes (la première résultant de la croissance de la fonction carré surR
|x+y|?|x|+|y|?|x+y| 2 ?(|x|+|y|) 2 ?x 2 +y 2 +2xy?|x| 2 +|y| 2 +2|x||y| ?x 2 +y 2 +2xy?x 2 +y 2 +2|x||y| ?2xy?2|x||y| ?xy?|x||y| cette dernière inégalité étant vraie, la première est aussi vraie.Résoudre dansR,|x+1|=4-|3x+2|.
Exercice 4(???).
Solution.
On a les équivalences suivantes :
x+1?0?x?-1 et3x+2?0?x?-2
3.On distingue alors trois cas :
Sur]-∞;-1].
|x+1|=4-|3x+2|?-(x+1)=4-(-(3x+2)) ?-x-1=4+3x+2 ?-4x=7 ?x=-74?]-∞;-1].
Sur?
1;-2 3? |x+1|=4-|3x+2|?x+1=4-(-(3x+2)) ?x+1=4+3x+2 ?-2x=5 ?x=-5 2??1;-23?
Sur?
-23;+∞?
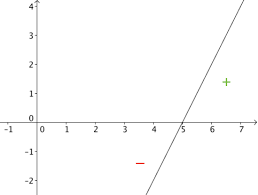
|x+1|=4-|3x+2|?x+1=4-(3x+2) ?x+1=4-3x-2 ?4x=1 ?x=1 4?? -23;+∞?Au final,S=?
-7 4;14? Ceci est confirmé par la lecture graphique suivante : 7 71. Calculs algébriques élémentaires
2. Résolution d"équations et d"inéquations polynomiales
Lorsque l"on veut résoudre une équation polynomiale de degré supérieur ou égal à 2, l"idée est de factoriser
et d"utiliser la propriété du produit nul. Or pour cela, il faut commencer par avoir un second membre (le
membre de droite de l"égalité) nul. Etainsi, résoudre l"équation revientà chercher les racines (si elles existent)
du polynôme formé par le premier membre. Nous allons voir quelques cas où on sait factoriser à commencer
par le cas classique du second degré : Soit(E)uneéquationdelaformeax
2 dansRrevient à chercher les racines de la fonction polynôme définie parP(x)=ax 2 +bx+c. Pour cela, on utilise le discriminant,Δ=b 2 -4ac,deP:1. SiΔ>0, alorsPadmet deux racinesx
1 =-b-? 2aetx 2 =-b+? 2a.On a alors :P(x)=a(x-x
1 )(x-x 2 ) pour toutxréel.2. SiΔ=0, alorsPadmet une unique racine (double)x
0 =-b 2a.On a alors :P(x)=a(x-x
0 2 pour toutxréel.3. SiΔ<0,Pn"a pas de racine réelle.
Application : exercices 1 et 3.
Rappel de cours(Résolution d"une équation de degré 2).En effet, notonsPla fonction polynôme de degrén?2 que l"on cherche à factoriser. Si on constate
de degrén-1. On a donc "abaissé" le degré de l"équation.Application : exercice 2.
Méthode 1(Comment résoudre une équation polynomiale de dégré supérieur ou égal à 3?).
8 81. Calculs algébriques élémentaires
Pour résoudre une inéquation polynomiale, la stratégie est la même que pour une équation : on se
ramène à un second membre nul et on factorise. Ensuite, il reste juste à étudier le signe de chaque
facteur, à consigner les informations dans un tableau de signes (en utilisant la règle des signes
pour un produit ou un quotient) et à conclure.Application : exercice 4.
Méthode 2(Comment résoudre une inéquation polynomiale?).Résoudre dansR,(E):|x
2 -2x+3|=2.Exercice 1(?).
Solution.
|x 2 -2x+3|=2??x 2 -2x+3=2oux 2 -2x+3=-2.Résolution dex
2 -2x+3=2. x 2 -2x+3=2?x 2 -2x+1=0?(x-1) 2 =0?x=1.La seule solution dex
2 -2x+3=2est1.Résolution dex
2 -2x+3=-2. x 2 -2x+3=-2?x 2 -2x+5=0. On poseP(x)=x 2 -2x+5 et on calcule son discriminant :Δ=-16. Ainsi le polynômePn"a aucune racine réelle et donc l"équationx 2 -2x+3=-2 n"a pas de solution réelle.Au final, l"ensemble solution de (E) estS={1}.
SoitP(x)=x
3 -x 2 -4x+4.1. Déterminer une racine évidente deP.
2. Déterminer alors la factorisation deP.
3. RésoudreP(x)>0.
Exercice 2(??).
Solution.
1. On remarque queP(1)=0 donc 1 est une racine évidente deP.
2. Ainsi, il existe une fonction polynômeQde degré 2 telle queP(x)=(x-1)Q(x) et on peut donc écrire qu"il
existe trois réelsa,betctels queP(x)=(x-1)(ax 2 +bx+c).Or, (x-1)(ax
2 +bx+c)=ax 3 +(b-a)x 2 +(c-b)x-c.Comme deux polynômes sont égaux si, et seulement si, ils ont les mêmes coefficients, par identification,
on trouve :? ??a=1 b-a=-1 c-b=-4 -c=4 et on obtienta=1,b=0etc=-4.DoncP(x)=(x-1)(x
2 -4)=(x-1)(x-2)(x+2). 9 91. Calculs algébriques élémentaires
3. On obtient le tableau de signes suivant :
x x-1 x-2 x+2 P(x) -∞-21 2+∞ 0++ 0+ 0++0+0+0-0+
Ainsi, l"ensemble solution deP(x)>0estS=]-2;1[?]2 ;+∞[.Résoudre dansRl"équation (E):x
4 +2x 2 -1=2 (on pourra penser à utiliser le changement de variableX=x 2Exercice 3(??).
Solution.
x 4 +2x 2 -1=2?x 4 +2x 2 -3=0.On poseX=x
2 et on cherche les racines dePoùP(X)=X 2 +2X-3. Or,Δ P =16>0doncPadmet deux racines distinctesX 1 =-3etX 2 =1. OrX=x 2 ?0 donc on ne conserve que la racine positive deP.On cherche alors les valeurs dextelles quex
2 =1. L"ensemble solution de (E) est doncS={-1 ; 1}.Remarque.Les équations de degré 4 ne faisant intervenir que des puissances paires dexsont appelées des
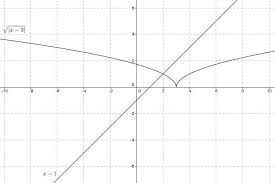
équations bi-carrées et se résolvent toujours en faisant le changement de variablesX=x 2 ce qui permet de se ramener à une équation de degré 2.Résoudre dansR,?|x-3|?x-1.
Exercice 4(???).
Solution.
On remarque tout d"abord que sur ]-∞;1[,x-1<0 donc il n"y a pas de solution sur cet intervalle puisque?
|x-3|?0.On cherche donc uniquement des solutions sur l"intervalle [1 ;+∞[. Sur cet intervalle, les deux membres sont
positifs, et donc on peut utiliser la croissance de la fonction carrée surR |x-3|?x-1?|x-3|?(x-1) 2quotesdbs_dbs31.pdfusesText_37[PDF] roman histoire d'amour pdf
[PDF] belles histoires damour courtes pdf
[PDF] histoire d'amour courte pdf
[PDF] la lettre amicale 3eme année exemple
[PDF] la lettre amicale 3eme annee passerelle francais
[PDF] exemple d'une lettre persuasive
[PDF] lettres d'amour des grands hommes livre
[PDF] poeme d amour en francais pdf
[PDF] citation amour pdf
[PDF] modèles de lettres administratives pdf
[PDF] écrire une lettre de motivation en espagnol
[PDF] la lettre personnelle familial
[PDF] forme de lettre administrative
[PDF] la lettre personnelle pdf
