 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Mathematics Worksheet. Worksheet # 12 Application of Derivatives # 1. Rate of Change. (Chapter – 6 : Application of Derivatives). Page 1
 Applications of differentiation
Applications of differentiation
The derivative of the function can be used to determine when a local maximum or local minimum occurs. Theorem (First derivative test). Let f be a differentiable
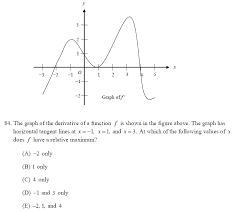 AP Calculus AB Review Week 3 Applications of Derivatives
AP Calculus AB Review Week 3 Applications of Derivatives
Applications of Derivatives. Brief Review. It is important in Calculus to study the application of derivatives to the understanding of the characteristics of
 Applications of Derivatives: Displacement Velocity and Acceleration
Applications of Derivatives: Displacement Velocity and Acceleration
Applications of Derivatives: Displacement. Velocity and Acceleration. Kinematics is the study of motion and is closely related to calculus. Physical
 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Mathematics Worksheet. Worksheet # 14 Application of Derivatives # 3. Tangents & Normals. (Chapter – 6 : Application of Derivatives). Page 1
 Class XII Mathematics.pdf
Class XII Mathematics.pdf
6.Applications of Derivatives 3 3 1 2 1 4. 0. 9. 7.Integrals. 2 2 2 4 1 4. 0. 10. 8.Applications of the. Integrals. 0. 0. 0 1 6. 6. 9.Vectors. 2 2 1 2. 0. 0. 4.
 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Worksheet # 15 Application of Derivatives # 4. Errors & Approximations. (Chapter – 6 : Application of Derivatives). Page 1
 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Worksheet # 17 Application of Derivatives # 6. Maxima & Minima # 2. (Chapter – 6 : Application of Derivatives). Page 1
 Applications of Derivatives Worksheet Name I. Velocity and
Applications of Derivatives Worksheet Name I. Velocity and
Applications of Derivatives Worksheet. Name. I. Velocity and Acceleration a. To find the velocity take the derivative of the position function.
 APPLICATION OF DERIVATIVES
APPLICATION OF DERIVATIVES
Working rule for finding points of local maxima or local minima: (a). First derivative test: (i). If f ′ (x) changes sign
 Application of Derivatives.pmd
Application of Derivatives.pmd
With the Calculus as a key Mathematics can be successfully applied In this chapter
 Applications of Differentiation
Applications of Differentiation
In this chapter we explore many applications Using First Derivatives to Classify Maximum and Minimum Values and Sketch Graphs ... p20-569.pdf.).
 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Worksheet # 17 Application of Derivatives # 6. Maxima & Minima # 2. (Chapter – 6 : Application of Derivatives). Page 1
 Applications of Derivatives: Displacement Velocity and Acceleration
Applications of Derivatives: Displacement Velocity and Acceleration
Applications of Derivatives: Displacement. Velocity and Acceleration. Kinematics is the study of motion and is closely related to calculus.
 2.7 Applications of Derivatives to Business and Economics
2.7 Applications of Derivatives to Business and Economics
Among the mathematical methods employed is calculus. In this section we illustrate just a few of the many applications of calculus to business and.
 Applications of differentiation
Applications of differentiation
Applications of differentiation – A guide for teachers (Years 11–12) The derivative of the function can be used to determine when a local maximum or ...
 Calculus and Its Applications (2-downloads)
Calculus and Its Applications (2-downloads)
2.4 Using Derivatives to Find Absolute Maximum and Minimum Values. 250. 2.5 Maximum–Minimum Problems;. Business and Economics Applications 262.
 INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
INDIAN SCHOOL DARSAIT Class XII Mathematics Worksheet
Mathematics Worksheet. Worksheet # 13 Application of Derivatives # 2. Increasing & Decreasing Functions. (Chapter – 6 : Application of Derivatives).
 MATH 34B WORKSHEET 3 SOLUTIONS I. Applications of derivatives.
MATH 34B WORKSHEET 3 SOLUTIONS I. Applications of derivatives.
Applications of derivatives. 1. (Bacterial growth) The population P of a bacterial colony t days after observation begins is modeled by the quadratic function.
 Class XII Chapter 6- Application of Derivatives Topic – Tangents and
Class XII Chapter 6- Application of Derivatives Topic – Tangents and
Chapter 6- Application of Derivatives. Topic – Tangents and Normals. Worksheet (Basic). 1. The slope of the normal to the curve y = 3x4 – 4x at x = 4 is—(1).
In this chapter, we explore many applications
of differentiation. We learn to �nd maximum and minimum values of functions, and that skill allows us to solve many kinds of problems in which we need to �nd the largest and/or smallest value in a real-world situation. Our differentiation skills will be applied to graphing, and we will use differentials to approximate function values. We will also use differentiation to explore elasticity of demand and related rates.2.1 Using First Derivatives to Classify Maximum
and Minimum Values and Sketch Graphs2.2 Using Second Derivatives to Classify Maximum and Minimum Values and Sketch Graphs
2.3 Graph Sketching: Asymptotes and Rational Functions
2.4 Using Derivatives to Find Absolute Maximum and Minimum Values
2.5 Maximum-Minimum Problems; Business, Economics, and General Applications
2.6 Marginals and Differentials
2.7 Elasticity of Demand
2.8 Implicit Differentiation and Related RatesApplications of Di�erentiation
2Minimizing Cost:
Minimizing cost is a common goal in
manufacturing. For example, cylindrical food cans come in a variety of sizes. Suppose a soup can is to have a volume of250 cm
3 The cost of material for the two circular ends is $0.0008>cm 2 , and the cost of material for the side is $0.0015 >cm 2 . What dimensions minimize the cost of material for the soup can? (This problem appears as Example 3 in Section 2.5. 188C r
Cost (in dollars)
Radius (in centimeters)ry
864200.32 0.24 0.16 0.08 (4.21, 0.2673)M02_BITT9391_11_SE_C02.1.indd 18829/10/14 4:39 PM
2.1 ? Using First Derivatives to Classify Maximum and Minimum Values and Sketc�h Graphs 189
Using First Derivatives to Classify
Maximum and Minimum Values
and Sketch Graphs The graph below shows a typical life cycle of a retail product and is similar to graphs we will consider in this chapter. Note that the number of items sold varies with re- spect to time. Sales begin at a small level and increase to a point of maximum sales, after which they taper off to a low level, possibly because of new competitive prod- ucts. The company then rejuvenates the product by making improvements. Think about versions of certain products: televisions can be traditional, �at-screen, or high- de�nition; music recordings have been produced as phonograph (vinyl) records, au diotapes, compact discs, and MP3 �les. Where might each of these products be in a typical product life cycle? Is the curve below appropriate for each product?PRODUCT LIFE CYCLE
Introduction Growth Maturity DeclineRejuvenation
S t TimeSales of product
Finding the largest and smallest values of a function - that is, the maximum and minimum values - has extensive applications. The first and second derivatives of a function can provide information for graphing functions and finding maximum and minimum values.Increasing and Decreasing Functions
If the graph of a function rises from left to right over an intervalI, the function is said
to be increasing on, or over, I. If the graph drops from left to right, the function is said to be decreasing on, or over, I. y x aIf the input
is less than the input then the output for is less than the output for .bIncreasing
f(a)f(b) f y x agbDecreasing
g(b)g(a)If the input
a is less than the input b, then the output for a is greater than the output for b 2.1 M02_BITT9391_11_SE_C02.1.indd 18929/10/14 4:39 PM190 CHAPTER 2 � Applications of Differentiation
Graph the function
f 1x2=- 1 3 x 3 +6x 2 -11x-50 and its derivative f1x2=-x
2 +12x-11 using the window3-10, 25,
-100, 1504, with Xscl=5 andYscl=25. Then traCe from left
to right along each graph. Mov- ing the cursor from left to right, note that the x-coordinate always increases. If the function is increasing, the y-coordinate will increase as well. If a function is decreasing, the y-coordinate will decrease.Over what intervals is
f increasing? Over what intervals is f decreasing? Over what intervals is f positive? Over what intervals is f negative? What rules might relate the sign of f to the behavior of f?TECHNOLOGY
CONNECTION
DEFINITIONS
A function
f is over I if, for every a and b in I, if a6b, then f1a26f1b2.A function
f is over I if, for every a and b in I, if a6b, then f1a27f1b2. The above de�nitions can be restated in terms of secant lines as shown below.Increasing:
f1b2-f1a2 b-a70. Decreasing: f
1b2-f1a2
b-a 60.f(b) a xy f
Slope of secantline is positive.
f(a) b f(a) a xy fSlope of secantline is negative. f(b) b The following theorem shows how we can use the derivative (the slope of a tan- gent line) to determine whether a function is increasing or decreasing.THEOREM 1
Let f be differentiable over an open interval I. If f1x270 for all x in I, then f is increasing over I. If f1x260 for all x in I, then f is decreasing over I. Theorem 1 is illustrated in the following graph of f1x2= 1 3 x 3 -x+ 2 3±2y
x(1, 0) f x )= x 3± x+
increasing f9(x) > 0Decreasing f9(x) < 0 ±1 increasing f9(x) > 01 ±32 ±3
±1,
4 ±3
1 f is increasing over the intervals (± , ±1) and (1, ); slopes of tangent lines are positive. f is decreasing over the interval (±1, 1);
slopes of tangent lines are negative. Note in the graph above that x=-1 and x=1 are not included in any interval over which the function is increasing or decreasing. These values are examples of critical values.We can de�ne these concepts as follows. M02_BITT9391_11_SE_C02.1.indd 19029/10/14 4:39 PM2.1 ? Using First Derivatives to Classify Maximum and Minimum Values and Sketc�h Graphs 191
Critical Values
Consider the following graph of a continuous function f. c 1 c 2 y x c 3 c 4 c 5 c 6 c 7 c 8 fNote the following:
1. f1x2=0 at x=c 1 , c 2 , c 4 , c 7 , and c 8 . That is, the tangent line to the graph is horizontal for these values. 2. f1x2 does not exist at x=c 3 , c 5 , and c 6 . The tangent line is vertical at c 3 and there are corners at both c 5 and c 6 . (See also the discussion at the end ofSection 1.4.)
A critical value of a function f is any number c in the domain of f for which the tangent line at 1 c, f1c22 is horizontal or for which the derivative does not exist.That is,
c is a critical value if f1c2 exists and f1c2=0 or f1c2 does not exist.Thus, in the graph of
f above: c 1 , c 2 , c 4 , c 7 , and c 8 are critical values because f1c2=0 for each value. c 3 , c 5 , and c 6 are critical values because f1c2 does not exist for each value. A continuous function can change from increasing to decreasing or from decreas- ing to increasing only at a critical value. In the above graph, c 1 , c 2 , c 4 , c 5 , c 6 , and c 7 separate intervals over which the function f increases from those in which it decreases or intervals in which the function decreases from those in which it in- creases. Although c 3 and c 8 are critical values, they do not separate intervals over which the function changes from increasing to decreasing or from decreasing to increasing. M02_BITT9391_11_SE_C02.1.indd 19129/10/14 4:39 PM192 CHAPTER 2 � Applications of Differentiation
Finding Relative Maximum and Minimum Values
Now consider a graph with "peaks" and "valleys" at x=c 1 , c 2 , and c 3 fquotesdbs_dbs21.pdfusesText_27[PDF] applications of graph theory in medicine
[PDF] applications of iir filter
[PDF] applications of inductive effect pdf
[PDF] applications of limits and derivatives
[PDF] applications of limits and derivatives in real life
[PDF] applications of minimum spanning tree
[PDF] applications of molecular spectroscopy pdf
[PDF] applications of numerical methods in civil engineering ppt
[PDF] applications of numerical methods in real life pdf
[PDF] applications of object oriented programming
[PDF] applications of online quiz system
[PDF] applications of powder metallurgy in aerospace
[PDF] applications of social learning theory in the classroom
[PDF] applications of software engineering in real life
