Corrigés des exercices
e ∧ ¬e. Or d'après les tables de vérité de ces formules (cf. corrigé de l'exercice 34)
Feuille dexercices no 2 1 Implication réciproque
https://www.math.ens.psl.eu/~pgervais/Documents/2019/MPInt1/TD2.pdf
Version corrigée Fiche dexercices - CH12 Logique et rédaction
La contraposée de cette proposition est « si un cosmonaute ne porte pas de chemise rouge alors il n'est pas américain »
Walanta
Par exemple en écrivant la contraposée de : F est un fermé ⇒ "il existe un point de F tel que : il n'existe aucun intervalle ouvert centré en ce point et
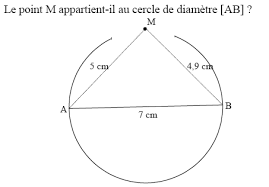TD : Exercices de logique
Ecrire la contraposée de la proposition P. 3. Démontrer qu'un entier Exercice 23 Résoudre le problème suivant en utilisant un raisonnement par l'absurde.
Exercices sur les différents types de raisonnements Pour tous ces
Corrigé. Exercice 1. Première rédaction possible : Tous les entiers peuvent se 1) Par contraposée : la contraposée est si a pair alors a² + 9. Si a est pair ...
Exercices de mathématiques - Exo7
Exercice 11. Soient E et F deux ensembles f : E → F. Démontrer que : ∀A
Exercices de mathématiques - Exo7
contraposée. Exercice 54. Montrer que √2 /∈ Q. [000148]. Exercice 55. Soit X ... exercices du chapitre celles qui sont des cas particuliers d'écrasements de ...
Cours dAlgèbre I et II avec Exercices CorrigésOM DE VOTRE
5)La contraposée de l'implication Soit P Q deux propositions
Exercices corrigés darithmétique
c) En déduire l'ensemble des solutions de (E). corrigé devoir n°4. Exercice 1. Théorème de Bezout. Soit a et b des entiers relatifs non nuls a
Exercices de mathématiques - Exo7
Montrer par contraposition les assertions suivantes E étant un ensemble : Dans ce corrigé
TD : Exercices de logique
raisonnement par récurrence par l'absurde
Exercices de mathématiques - Exo7
Exercice 10 Le missionnaire et les cannibales Exercice 22. Montrer par contraposition les assertions suivantes E étant un ensemble :.
Démontrer une implication ou une équivalence - %©NPOUSFS VOF
Soit n ? N. Montrer que si n est impair alors n2 est impair. 1PVS WPVT BJEFS E©NBSSFS. EXERCICE 1.1.
Logique.pdf
pratique et en particulier à bien maîtriser les quelques exercices corrigés. 3.5.3 Négation contraposée et réciproque d'une implication .
Cours dAlgèbre I et II avec Exercices CorrigésOM DE VOTRE
une partie exercices corrigés dont la plupart ont été proposé dans le 5)La contraposée de l'implication Soit P Q deux propositions
Correction des exercices du TD1
l'exercice 1 il se peut que le rédacteur fasse quelques raccourcis ; cela ne vous autorise La contraposée est une forme équivalente de l'implication :.
Logique Travaux Dirigés - Partie 3 Corrigés
Les exercices sont de difficultés diverses et sont à traiter en se basant aurait fait : ¬D ?? V (seule possibilité) donc (contraposée) ¬C ?? V
Daniel ALIBERT cours et exercices corrigés volume 1
Démontrer que p est surjective. Les applications S et C sont-elles injectives ? exercice 16. Soit E un ensemble. On appelle "
Exercices corrigés Théor`eme de Rolle accroissements finis
g(x) = e. Solution de l'exercice 11. On consid`ere la propriété. (?n) fg est au moins n
[PDF] Feuille dexercices no 2 1 Implication réciproque contraposée
1 Implication réciproque contraposée 1 1 Retour sur l'implication Dans ce paragraphe A et B désignent des propositions Revenons sur
[PDF] Logique ensembles raisonnements - Exo7
Exercice 10 Montrer par contraposition les assertions suivantes E étant un ensemble : 1 ?AB ? ?(E) (A?B = A?B) ? A = B 2
Contraposée dune implication exercice corrigé 01 - YouTube
14 oct 2020 · prof_lechab Contraposée d'une implication exercice corrigé raisonnement par contraposéeEn Durée : 5:00Postée : 14 oct 2020
[PDF] Correction des exercices du TD1 - UTC
Q4 : Comparaison des résultats des questions 1 et 3 La contraposée est équivalente à l'implication de départ Il est donc normal de retrouver le même résultat
[PDF] Logique - Licence de mathématiques Lyon 1
Aller à : Correction exercice 1 : Donner leur contraposée et leur négation Donner la négation et la contraposée de cette phrase logique
[PDF] 1BAC BIOF - AlloSchool
Exercice 2 Ecrire à l'aide de quantificateurs les propositions suivantes : Le raisonnement par contraposition est basé sur l'équivalence suivante :
[PDF] Exercices avec corrections sur la logique - AlloSchool
Exercice 1 Ecrire les contraposées des implications suivantes et les démontrer n est un entier naturel x et y sont des nombres réels 1 n premier ? n = 2 ou
Logique et raisonnement exercices corrigés 1 bac
16 sept 2021 · Exercice 4 (Logique et raisonnement exercices corrigés 1 bac) Résoudre dans ? l'équation suivante (E) : ?2x2 ? x ? 6? ? ?x +
![[PDF] Logique ensembles raisonnements - Exo7](https://pdfprof.com/Listes/17/45341-17fic00002.pdf.pdf.jpg "[PDF] Logique ensembles raisonnements - Exo7")
Exo7 Logique, ensembles, raisonnements
1 Logique
Exercice 1Compléter les pointillés par le connecteur logique qui s"impose :,;(;):1.x2Rx2=4::::::x=2 ;
2.z2Cz=z::::::z2R;
3.x2Rx=p::::::e2ix=1.
Soient les quatre assertions suivantes :
(a)9x2R8y2Rx+y>0 ;(b)8x2R9y2Rx+y>0 ; (c)8x2R8y2Rx+y>0 ;(d)9x2R8y2Ry2>x: 1. Les assertions a,b,c,dsont-elles vraies ou fausses ? 2.Donner leur nég ation.
DansR2, on définit les ensemblesF1=f(x;y)2R2;y60getF2=f(x;y)2R2;xy>1;x>0g. On note M1M2la distance usuelle entre deux pointsM1etM2deR2. Évaluer les propositions suivantes :
1.8e2]0;+¥[9M12F19M22F2M1M2 2.9M12F19M22F28e2]0;+¥[M1M2 3.9e2]0;+¥[8M12F18M22F2M1M2 4.8M12F18M22F29e2]0;+¥[M1M2 Quand elles sont fausses, donner leur négation. Nier la proposition: "tous les habitants de la rue du Havre qui ont les yeux bleus gagneront au loto et prendront
leur retraite avant 50 ans". Nier les assertions suivantes :
1 1.tout triangle rectangle possède un angle droit ;
2. dans toutes les écuries, tous les che vauxsont noirs ; 3. pour tout entier x, il existe un entierytel que, pour tout entierz, la relationz z4.8e>09a>0(jx7=5j Soientf;gdeux fonctions deRdansR. Traduire en termes de quantificateurs les expressions suivantes : 1.fest majorée;
2.fest bornée;
3.fest paire;
4.fest impaire;
5.fne s"annule jamais;
6.fest périodique;
7.fest croissante;
8.fest strictement décroissante;
9.fn"est pas la fonction nulle;
10.fn"a jamais les mêmes valeurs en deux points distincts;
11.fatteint toutes les valeurs deN;
12.fest inférieure àg;
13.fn"est pas inférieure àg.
Soitfune application deRdansR. Nier, de la manière la plus précise possible, les énoncés qui suivent :
1. Pour tout x2Rf(x)61.
2. L "applicationfest croissante.
3. L "applicationfest croissante et positive.
4. Il e xistex2R+tel quef(x)60.
5. Il e xistex2Rtel que quel que soity2R, sixf(y). On ne demande pas de démontrer quoi que ce soit, juste d"écrire le contraire d"un énoncé.
Montrer que
8e>09N2Ntel que(n>N)2e<2n+1n+2<2+e):
2 Ensembles
Exercice 9SoitA;Bdeux ensembles, montrer{(A[B) ={A\{Bet{(A\B) ={A[{B. Montrer par contraposition les assertions suivantes,Eétant un ensemble : 1.8A;B2P(E) (A\B=A[B))A=B,
2.8A;B;C2P(E) (A\B=A\CetA[B=A[C))B=C.
SoientEetFdeux ensembles,f:E!F. Démontrer que : 8A;B2P(E) (AB))(f(A)f(B)),
8A;B2P(E)f(A\B)f(A)\f(B),
8A;B2P(E)f(A[B) =f(A)[f(B),
8A;B2P(F)f1(A[B) =f1(A)[f1(B),
8A2P(F)f1(FnA) =Enf1(A).
Montrez que chacun des ensembles suivants est un intervalle que vous calculerez. I=+¥\
n=1 1n ;2+1n etJ=+¥[ n=2 1+1n ;n Exercice 13Soit(fn)n2Nune suite d"applications de l"ensembleNdans lui-même. On définit une applicationfdeNdans
Nen posantf(n) =fn(n)+1. Démontrer qu"il n"existe aucunp2Ntel quef=fp. 1. Soit p1;p2;:::;pr,rnombres premiers. Montrer que l"entierN=p1p2:::pr+1 n"est divisible par aucun des entierspi. 2. Utiliser la question précédente pour montrer par l"absurde qu"il e xisteune infinité de nombres premiers.
4 Récurrence
Exercice 15Montrer :
1. nå k=1k=n(n+1)2 8n2N: 2. nå k=1k2=n(n+1)(2n+1)6 8n2N: SoitXun ensemble. Pourf2F(X;X), on définitf0=idet par récurrence pourn2Nfn+1=fnf. 1. Montrer que 8n2Nfn+1=ffn.
2. Montrer que si fest bijective alors8n2N(f1)n= (fn)1. Soit la suite(xn)n2Ndéfinie parx0=4 etxn+1=2x2n3x n+2. 1. Montrer que : 8n2Nxn>3.
2. Montrer que : 8n2Nxn+13>32
(xn3). 3. Montrer que : 8n2Nxn>32
n+3. 4. La suite (xn)n2Nest-elle convergente ?
Indication pourl"exer cice2 NAttention : la négation d"une inégalité stricte est une inégalité large (et réciproquement).
Indication pour
l"exer cice 3 NFaire un dessin deF1et deF2. Essayer de voir si la difficulté pour réaliser les assertions vient dee"petit"
(c"est-à-dire proche de 0) ou dee"grand" (quand il tend vers+¥).Indication pourl"exer cice8 NEn fait, on a toujours :
2n+1n+262. Puis chercher une condition surnpour que l"inégalité
2e<2n+1n+2
soit vraie.Indication pourl"exer cice9 NIl est plus facile de raisonner en prenant un élémentx2E. Par exemple, soitF;Gdes sous-ensembles deE.
Montrer queFGrevient à montrer que pour toutx2Falorsx2G. Et montrerF=Gest équivalent àx2F si et seulement six2G, et ce pour toutxdeE. Remarque : pour montrerF=Gon peut aussi montrerFG puisGF. Enfin, se rappeler quex2{Fsi et seulement six=2F.Indication pourl"exer cice13 NPar l"absurde, supposer qu"il existep2Ntel quef=fp. Puis pour un telp, évaluerfetfpen une valeur bien
choisie.Indication pourl"exer cice14 NPour la première question vous pouvez raisonner par contraposition ou par l"absurde.
Indication pour
l"exer cice 16 NPour les deux questions, travailler par récurrence.
Indication pour
l"exer cice 17 N1.Récurrence : calculer xn+13.
2. Calculer xn+1332
(xn3). 3. Récurrence. 5
Correction del"exer cice1 N1.(
2., 3.)Correction del"exer cice2 N1.(a) est f ausse.C arsa nég ationqui est 8x2R9y2Rx+y60 est vraie. Étant donnéx2Ril existe
toujours uny2Rtel quex+y60, par exemple on peut prendrey=(x+1)et alorsx+y=xx1= 160.
2. (b) est vraie, pour un xdonné, on peut prendre (par exemple)y=x+1 et alorsx+y=1>0. La négation de (b) est9x2R8y2Rx+y60. 3. (c) : 8x2R8y2Rx+y>0 est fausse, par exemplex=1,y=0. La négation est9x2R9y2 Rx+y60.
4. (d) est vraie, on peut prendre x=1. La négation est:8x2R9y2Ry26x.Correction del"exer cice3 N1.Cette proposition est vraie. En ef fetsoit e>0, définissonsM1= (2e
;0)2F1etM2= (2e ;e2 )2F2, alors M 1M2=e2
0 la proposition est donc démontrée. 2. Soit deux points fixés M1,M2vérifiant cette proposition, la distanced=M1M2est aussi petite que l"on
veut donc elle est nulle, doncM1=M2; or les ensemblesF1etF2sont disjoints. Donc la proposition est fausse. La négation de cette proposition est : 8M12F18M22F29e2]0;+¥[M1M2>e
et cela exprime le fait que les ensemblesF1etF2sont disjoints. 3. Celle ci est ég alementf ausse,en ef fetsupposons qu"elle soit vraie, soit alors ecorrespondant à cette
proposition. SoitM1= (e+2;0)etM2= (1;1), on aM1M2>e+1 ce qui est absurde. La négation est : 8e2]0;+¥[9M12F19M22F2M1M2>e
C"est-à-dire que l"on peut trouver deux points aussi éloignés l"un de l"autre que l"on veut.
4. Cette proposition est vraie, il suf fitde choisir e=M1M2+1. Elle signifie que la distance entre deux points donnés est un nombre fini !Correction del"exer cice4 N"Il existe un habitant de la rue du Havre qui a les yeux bleus, qui ne gagnera pas au loto ou qui prendra sa
retraite après 50 ans."Correction del"exer cice5 N1."Il e xisteun triangle rectangle qui n"a pas d"angle droit." Bien sûr cette dernière phrase est f ausse!
2. "Il e xisteune écurie dans laquelle il y a (au moins) un che valdont la couleur n"est pas noire." 6 3.Sachant que la proposition en lang agemathématique s"écrit
8x2Z9y2Z8z2Z(z la négation est 9x2Z8y2Z9z2Z(zx+1):
4.9e>08a>0(jx7=5je):Correction del"exer cice6 N1.9M2R8x2Rf(x)6M;
2.9M2R9m2R8x2Rm6f(x)6M;
3.8x2Rf(x) =f(x);
4.8x2Rf(x) =f(x);
5.8x2Rf(x)6=0;
6.9a2R8x2Rf(x+a) =f(x);
7.8(x;y)2R2(x6y)f(x)6f(y));
8.8(x;y)2R2(xf(y));
9.9x2Rf(x)6=0;
10.8(x;y)2R2(x6=y)f(x)6=f(y));
11.8n2N9x2Rf(x) =n;
12.8x2Rf(x)6g(x);
13.9x2Rf(x)>g(x).Correction del"exer cice7 NDans ce corrigé, nous donnons une justification, ce qui n"était pas demandé.
1. Cette assertion se décompose de la manière sui vante: ( Pour tout x2R) (f(x)61). La négation de "(
Pour toutx2R)" est "Il existex2R" et la négation de "(f(x)61)" estf(x)>1. Donc la négation de l"assertion complète est : "Il existex2R;f(x)>1". 2. Rappelons comment se traduit l"assertion "L "applicationfest croissante" : "pour tout couple de réels
(x1;x2), six16x2alorsf(x1)6f(x2)". Cela se décompose en : "(pour tout couple de réelsx1etx2) (x16x2impliquef(x1)6f(x2))". La négation de la première partie est : "(il existe un couple de réels
(x1;x2))" et la négation de la deuxième partie est : "(x16x2etf(x1)>f(x2))". Donc la négation de
l"assertion complète est : "Il existex12Retx22Rtels quex16x2etf(x1)>f(x2)". 3. La négationest:"l"application fn"estpascroissanteoun"estpaspositive". Onadéjàtraduit"l"application
fn"est pas croissante", traduisons "l"applicationfn"est pas positive" : "il existex2R;f(x)<0". Donc la négation de l"assertion complète est : " Il existex12Retx22Rtels quex1f(x2), ou il existex2R;f(x)<0". 4. Cette assertion se décompose de la manière sui vante: "(Il e xistex2R+) (f(x)60)". La négation de la
première partie est : "(pour toutx2R+)", et celle de la seconde est :"(f(x)>0)". Donc la négation de
l"assertion complète est : "Pour toutx2R+,f(x)>0".quotesdbs_dbs29.pdfusesText_35
2.9M12F19M22F28e2]0;+¥[M1M2 3.9e2]0;+¥[8M12F18M22F2M1M2 4.8M12F18M22F29e2]0;+¥[M1M2 Quand elles sont fausses, donner leur négation. Nier la proposition: "tous les habitants de la rue du Havre qui ont les yeux bleus gagneront au loto et prendront
leur retraite avant 50 ans". Nier les assertions suivantes :
1 1.tout triangle rectangle possède un angle droit ;
2. dans toutes les écuries, tous les che vauxsont noirs ; 3. pour tout entier x, il existe un entierytel que, pour tout entierz, la relationz z4.8e>09a>0(jx7=5j Soientf;gdeux fonctions deRdansR. Traduire en termes de quantificateurs les expressions suivantes : 1.fest majorée;
2.fest bornée;
3.fest paire;
4.fest impaire;
5.fne s"annule jamais;
6.fest périodique;
7.fest croissante;
8.fest strictement décroissante;
9.fn"est pas la fonction nulle;
10.fn"a jamais les mêmes valeurs en deux points distincts;
11.fatteint toutes les valeurs deN;
12.fest inférieure àg;
13.fn"est pas inférieure àg.
Soitfune application deRdansR. Nier, de la manière la plus précise possible, les énoncés qui suivent :
1. Pour tout x2Rf(x)61.
2. L "applicationfest croissante.
3. L "applicationfest croissante et positive.
4. Il e xistex2R+tel quef(x)60.
5. Il e xistex2Rtel que quel que soity2R, sixf(y). On ne demande pas de démontrer quoi que ce soit, juste d"écrire le contraire d"un énoncé.
Montrer que
8e>09N2Ntel que(n>N)2e<2n+1n+2<2+e):
2 Ensembles
Exercice 9SoitA;Bdeux ensembles, montrer{(A[B) ={A\{Bet{(A\B) ={A[{B. Montrer par contraposition les assertions suivantes,Eétant un ensemble : 1.8A;B2P(E) (A\B=A[B))A=B,
2.8A;B;C2P(E) (A\B=A\CetA[B=A[C))B=C.
SoientEetFdeux ensembles,f:E!F. Démontrer que : 8A;B2P(E) (AB))(f(A)f(B)),
8A;B2P(E)f(A\B)f(A)\f(B),
8A;B2P(E)f(A[B) =f(A)[f(B),
8A;B2P(F)f1(A[B) =f1(A)[f1(B),
8A2P(F)f1(FnA) =Enf1(A).
Montrez que chacun des ensembles suivants est un intervalle que vous calculerez. I=+¥\
n=1 1n ;2+1n etJ=+¥[ n=2 1+1n ;n Exercice 13Soit(fn)n2Nune suite d"applications de l"ensembleNdans lui-même. On définit une applicationfdeNdans
Nen posantf(n) =fn(n)+1. Démontrer qu"il n"existe aucunp2Ntel quef=fp. 1. Soit p1;p2;:::;pr,rnombres premiers. Montrer que l"entierN=p1p2:::pr+1 n"est divisible par aucun des entierspi. 2. Utiliser la question précédente pour montrer par l"absurde qu"il e xisteune infinité de nombres premiers.
4 Récurrence
Exercice 15Montrer :
1. nå k=1k=n(n+1)2 8n2N: 2. nå k=1k2=n(n+1)(2n+1)6 8n2N: SoitXun ensemble. Pourf2F(X;X), on définitf0=idet par récurrence pourn2Nfn+1=fnf. 1. Montrer que 8n2Nfn+1=ffn.
2. Montrer que si fest bijective alors8n2N(f1)n= (fn)1. Soit la suite(xn)n2Ndéfinie parx0=4 etxn+1=2x2n3x n+2. 1. Montrer que : 8n2Nxn>3.
2. Montrer que : 8n2Nxn+13>32
(xn3). 3. Montrer que : 8n2Nxn>32
n+3. 4. La suite (xn)n2Nest-elle convergente ?
Indication pourl"exer cice2 NAttention : la négation d"une inégalité stricte est une inégalité large (et réciproquement).
Indication pour
l"exer cice 3 NFaire un dessin deF1et deF2. Essayer de voir si la difficulté pour réaliser les assertions vient dee"petit"
(c"est-à-dire proche de 0) ou dee"grand" (quand il tend vers+¥).Indication pourl"exer cice8 NEn fait, on a toujours :
2n+1n+262. Puis chercher une condition surnpour que l"inégalité
2e<2n+1n+2
soit vraie.Indication pourl"exer cice9 NIl est plus facile de raisonner en prenant un élémentx2E. Par exemple, soitF;Gdes sous-ensembles deE.
Montrer queFGrevient à montrer que pour toutx2Falorsx2G. Et montrerF=Gest équivalent àx2F si et seulement six2G, et ce pour toutxdeE. Remarque : pour montrerF=Gon peut aussi montrerFG puisGF. Enfin, se rappeler quex2{Fsi et seulement six=2F.Indication pourl"exer cice13 NPar l"absurde, supposer qu"il existep2Ntel quef=fp. Puis pour un telp, évaluerfetfpen une valeur bien
choisie.Indication pourl"exer cice14 NPour la première question vous pouvez raisonner par contraposition ou par l"absurde.
Indication pour
l"exer cice 16 NPour les deux questions, travailler par récurrence.
Indication pour
l"exer cice 17 N1.Récurrence : calculer xn+13.
2. Calculer xn+1332
(xn3). 3. Récurrence. 5
Correction del"exer cice1 N1.(
2., 3.)Correction del"exer cice2 N1.(a) est f ausse.C arsa nég ationqui est 8x2R9y2Rx+y60 est vraie. Étant donnéx2Ril existe
toujours uny2Rtel quex+y60, par exemple on peut prendrey=(x+1)et alorsx+y=xx1= 160.
2. (b) est vraie, pour un xdonné, on peut prendre (par exemple)y=x+1 et alorsx+y=1>0. La négation de (b) est9x2R8y2Rx+y60. 3. (c) : 8x2R8y2Rx+y>0 est fausse, par exemplex=1,y=0. La négation est9x2R9y2 Rx+y60.
4. (d) est vraie, on peut prendre x=1. La négation est:8x2R9y2Ry26x.Correction del"exer cice3 N1.Cette proposition est vraie. En ef fetsoit e>0, définissonsM1= (2e
;0)2F1etM2= (2e ;e2 )2F2, alors M 1M2=e2
0 la proposition est donc démontrée. 2. Soit deux points fixés M1,M2vérifiant cette proposition, la distanced=M1M2est aussi petite que l"on
veut donc elle est nulle, doncM1=M2; or les ensemblesF1etF2sont disjoints. Donc la proposition est fausse. La négation de cette proposition est : 8M12F18M22F29e2]0;+¥[M1M2>e
et cela exprime le fait que les ensemblesF1etF2sont disjoints. 3. Celle ci est ég alementf ausse,en ef fetsupposons qu"elle soit vraie, soit alors ecorrespondant à cette
proposition. SoitM1= (e+2;0)etM2= (1;1), on aM1M2>e+1 ce qui est absurde. La négation est : 8e2]0;+¥[9M12F19M22F2M1M2>e
C"est-à-dire que l"on peut trouver deux points aussi éloignés l"un de l"autre que l"on veut.
4. Cette proposition est vraie, il suf fitde choisir e=M1M2+1. Elle signifie que la distance entre deux points donnés est un nombre fini !Correction del"exer cice4 N"Il existe un habitant de la rue du Havre qui a les yeux bleus, qui ne gagnera pas au loto ou qui prendra sa
retraite après 50 ans."Correction del"exer cice5 N1."Il e xisteun triangle rectangle qui n"a pas d"angle droit." Bien sûr cette dernière phrase est f ausse!
2. "Il e xisteune écurie dans laquelle il y a (au moins) un che valdont la couleur n"est pas noire." 6 3.Sachant que la proposition en lang agemathématique s"écrit
8x2Z9y2Z8z2Z(z la négation est 9x2Z8y2Z9z2Z(zx+1):
4.9e>08a>0(jx7=5je):Correction del"exer cice6 N1.9M2R8x2Rf(x)6M;
2.9M2R9m2R8x2Rm6f(x)6M;
3.8x2Rf(x) =f(x);
4.8x2Rf(x) =f(x);
5.8x2Rf(x)6=0;
6.9a2R8x2Rf(x+a) =f(x);
7.8(x;y)2R2(x6y)f(x)6f(y));
8.8(x;y)2R2(xf(y));
9.9x2Rf(x)6=0;
10.8(x;y)2R2(x6=y)f(x)6=f(y));
11.8n2N9x2Rf(x) =n;
12.8x2Rf(x)6g(x);
13.9x2Rf(x)>g(x).Correction del"exer cice7 NDans ce corrigé, nous donnons une justification, ce qui n"était pas demandé.
1. Cette assertion se décompose de la manière sui vante: ( Pour tout x2R) (f(x)61). La négation de "(
Pour toutx2R)" est "Il existex2R" et la négation de "(f(x)61)" estf(x)>1. Donc la négation de l"assertion complète est : "Il existex2R;f(x)>1". 2. Rappelons comment se traduit l"assertion "L "applicationfest croissante" : "pour tout couple de réels
(x1;x2), six16x2alorsf(x1)6f(x2)". Cela se décompose en : "(pour tout couple de réelsx1etx2) (x16x2impliquef(x1)6f(x2))". La négation de la première partie est : "(il existe un couple de réels
(x1;x2))" et la négation de la deuxième partie est : "(x16x2etf(x1)>f(x2))". Donc la négation de
l"assertion complète est : "Il existex12Retx22Rtels quex16x2etf(x1)>f(x2)". 3. La négationest:"l"application fn"estpascroissanteoun"estpaspositive". Onadéjàtraduit"l"application
fn"est pas croissante", traduisons "l"applicationfn"est pas positive" : "il existex2R;f(x)<0". Donc la négation de l"assertion complète est : " Il existex12Retx22Rtels quex1f(x2), ou il existex2R;f(x)<0". 4. Cette assertion se décompose de la manière sui vante: "(Il e xistex2R+) (f(x)60)". La négation de la
première partie est : "(pour toutx2R+)", et celle de la seconde est :"(f(x)>0)". Donc la négation de
l"assertion complète est : "Pour toutx2R+,f(x)>0".quotesdbs_dbs29.pdfusesText_35
3.9e2]0;+¥[8M12F18M22F2M1M2 4.8M12F18M22F29e2]0;+¥[M1M2 Quand elles sont fausses, donner leur négation. Nier la proposition: "tous les habitants de la rue du Havre qui ont les yeux bleus gagneront au loto et prendront
leur retraite avant 50 ans". Nier les assertions suivantes :
1 1.tout triangle rectangle possède un angle droit ;
2. dans toutes les écuries, tous les che vauxsont noirs ; 3. pour tout entier x, il existe un entierytel que, pour tout entierz, la relationz z4.8e>09a>0(jx7=5j Soientf;gdeux fonctions deRdansR. Traduire en termes de quantificateurs les expressions suivantes : 1.fest majorée;
2.fest bornée;
3.fest paire;
4.fest impaire;
5.fne s"annule jamais;
6.fest périodique;
7.fest croissante;
8.fest strictement décroissante;
9.fn"est pas la fonction nulle;
10.fn"a jamais les mêmes valeurs en deux points distincts;
11.fatteint toutes les valeurs deN;
12.fest inférieure àg;
13.fn"est pas inférieure àg.
Soitfune application deRdansR. Nier, de la manière la plus précise possible, les énoncés qui suivent :
1. Pour tout x2Rf(x)61.
2. L "applicationfest croissante.
3. L "applicationfest croissante et positive.
4. Il e xistex2R+tel quef(x)60.
5. Il e xistex2Rtel que quel que soity2R, sixf(y). On ne demande pas de démontrer quoi que ce soit, juste d"écrire le contraire d"un énoncé.
Montrer que
8e>09N2Ntel que(n>N)2e<2n+1n+2<2+e):
2 Ensembles
Exercice 9SoitA;Bdeux ensembles, montrer{(A[B) ={A\{Bet{(A\B) ={A[{B. Montrer par contraposition les assertions suivantes,Eétant un ensemble : 1.8A;B2P(E) (A\B=A[B))A=B,
2.8A;B;C2P(E) (A\B=A\CetA[B=A[C))B=C.
SoientEetFdeux ensembles,f:E!F. Démontrer que : 8A;B2P(E) (AB))(f(A)f(B)),
8A;B2P(E)f(A\B)f(A)\f(B),
8A;B2P(E)f(A[B) =f(A)[f(B),
8A;B2P(F)f1(A[B) =f1(A)[f1(B),
8A2P(F)f1(FnA) =Enf1(A).
Montrez que chacun des ensembles suivants est un intervalle que vous calculerez. I=+¥\
n=1 1n ;2+1n etJ=+¥[ n=2 1+1n ;n Exercice 13Soit(fn)n2Nune suite d"applications de l"ensembleNdans lui-même. On définit une applicationfdeNdans
Nen posantf(n) =fn(n)+1. Démontrer qu"il n"existe aucunp2Ntel quef=fp. 1. Soit p1;p2;:::;pr,rnombres premiers. Montrer que l"entierN=p1p2:::pr+1 n"est divisible par aucun des entierspi. 2. Utiliser la question précédente pour montrer par l"absurde qu"il e xisteune infinité de nombres premiers.
4 Récurrence
Exercice 15Montrer :
1. nå k=1k=n(n+1)2 8n2N: 2. nå k=1k2=n(n+1)(2n+1)6 8n2N: SoitXun ensemble. Pourf2F(X;X), on définitf0=idet par récurrence pourn2Nfn+1=fnf. 1. Montrer que 8n2Nfn+1=ffn.
2. Montrer que si fest bijective alors8n2N(f1)n= (fn)1. Soit la suite(xn)n2Ndéfinie parx0=4 etxn+1=2x2n3x n+2. 1. Montrer que : 8n2Nxn>3.
2. Montrer que : 8n2Nxn+13>32
(xn3). 3. Montrer que : 8n2Nxn>32
n+3. 4. La suite (xn)n2Nest-elle convergente ?
Indication pourl"exer cice2 NAttention : la négation d"une inégalité stricte est une inégalité large (et réciproquement).
Indication pour
l"exer cice 3 NFaire un dessin deF1et deF2. Essayer de voir si la difficulté pour réaliser les assertions vient dee"petit"
(c"est-à-dire proche de 0) ou dee"grand" (quand il tend vers+¥).Indication pourl"exer cice8 NEn fait, on a toujours :
2n+1n+262. Puis chercher une condition surnpour que l"inégalité
2e<2n+1n+2
soit vraie.Indication pourl"exer cice9 NIl est plus facile de raisonner en prenant un élémentx2E. Par exemple, soitF;Gdes sous-ensembles deE.
Montrer queFGrevient à montrer que pour toutx2Falorsx2G. Et montrerF=Gest équivalent àx2F si et seulement six2G, et ce pour toutxdeE. Remarque : pour montrerF=Gon peut aussi montrerFG puisGF. Enfin, se rappeler quex2{Fsi et seulement six=2F.Indication pourl"exer cice13 NPar l"absurde, supposer qu"il existep2Ntel quef=fp. Puis pour un telp, évaluerfetfpen une valeur bien
choisie.Indication pourl"exer cice14 NPour la première question vous pouvez raisonner par contraposition ou par l"absurde.
Indication pour
l"exer cice 16 NPour les deux questions, travailler par récurrence.
Indication pour
l"exer cice 17 N1.Récurrence : calculer xn+13.
2. Calculer xn+1332
(xn3). 3. Récurrence. 5
Correction del"exer cice1 N1.(
2., 3.)Correction del"exer cice2 N1.(a) est f ausse.C arsa nég ationqui est 8x2R9y2Rx+y60 est vraie. Étant donnéx2Ril existe
toujours uny2Rtel quex+y60, par exemple on peut prendrey=(x+1)et alorsx+y=xx1= 160.
2. (b) est vraie, pour un xdonné, on peut prendre (par exemple)y=x+1 et alorsx+y=1>0. La négation de (b) est9x2R8y2Rx+y60. 3. (c) : 8x2R8y2Rx+y>0 est fausse, par exemplex=1,y=0. La négation est9x2R9y2 Rx+y60.
4. (d) est vraie, on peut prendre x=1. La négation est:8x2R9y2Ry26x.Correction del"exer cice3 N1.Cette proposition est vraie. En ef fetsoit e>0, définissonsM1= (2e
;0)2F1etM2= (2e ;e2 )2F2, alors M 1M2=e2
0 la proposition est donc démontrée. 2. Soit deux points fixés M1,M2vérifiant cette proposition, la distanced=M1M2est aussi petite que l"on
veut donc elle est nulle, doncM1=M2; or les ensemblesF1etF2sont disjoints. Donc la proposition est fausse. La négation de cette proposition est : 8M12F18M22F29e2]0;+¥[M1M2>e
et cela exprime le fait que les ensemblesF1etF2sont disjoints. 3. Celle ci est ég alementf ausse,en ef fetsupposons qu"elle soit vraie, soit alors ecorrespondant à cette
proposition. SoitM1= (e+2;0)etM2= (1;1), on aM1M2>e+1 ce qui est absurde. La négation est : 8e2]0;+¥[9M12F19M22F2M1M2>e
C"est-à-dire que l"on peut trouver deux points aussi éloignés l"un de l"autre que l"on veut.
4. Cette proposition est vraie, il suf fitde choisir e=M1M2+1. Elle signifie que la distance entre deux points donnés est un nombre fini !Correction del"exer cice4 N"Il existe un habitant de la rue du Havre qui a les yeux bleus, qui ne gagnera pas au loto ou qui prendra sa
retraite après 50 ans."Correction del"exer cice5 N1."Il e xisteun triangle rectangle qui n"a pas d"angle droit." Bien sûr cette dernière phrase est f ausse!
2. "Il e xisteune écurie dans laquelle il y a (au moins) un che valdont la couleur n"est pas noire." 6 3.Sachant que la proposition en lang agemathématique s"écrit
8x2Z9y2Z8z2Z(z la négation est 9x2Z8y2Z9z2Z(zx+1):
4.9e>08a>0(jx7=5je):Correction del"exer cice6 N1.9M2R8x2Rf(x)6M;
2.9M2R9m2R8x2Rm6f(x)6M;
3.8x2Rf(x) =f(x);
4.8x2Rf(x) =f(x);
5.8x2Rf(x)6=0;
6.9a2R8x2Rf(x+a) =f(x);
7.8(x;y)2R2(x6y)f(x)6f(y));
8.8(x;y)2R2(xf(y));
9.9x2Rf(x)6=0;
10.8(x;y)2R2(x6=y)f(x)6=f(y));
11.8n2N9x2Rf(x) =n;
12.8x2Rf(x)6g(x);
13.9x2Rf(x)>g(x).Correction del"exer cice7 NDans ce corrigé, nous donnons une justification, ce qui n"était pas demandé.
1. Cette assertion se décompose de la manière sui vante: ( Pour tout x2R) (f(x)61). La négation de "(
Pour toutx2R)" est "Il existex2R" et la négation de "(f(x)61)" estf(x)>1. Donc la négation de l"assertion complète est : "Il existex2R;f(x)>1". 2. Rappelons comment se traduit l"assertion "L "applicationfest croissante" : "pour tout couple de réels
(x1;x2), six16x2alorsf(x1)6f(x2)". Cela se décompose en : "(pour tout couple de réelsx1etx2) (x16x2impliquef(x1)6f(x2))". La négation de la première partie est : "(il existe un couple de réels
(x1;x2))" et la négation de la deuxième partie est : "(x16x2etf(x1)>f(x2))". Donc la négation de
l"assertion complète est : "Il existex12Retx22Rtels quex16x2etf(x1)>f(x2)". 3. La négationest:"l"application fn"estpascroissanteoun"estpaspositive". Onadéjàtraduit"l"application
fn"est pas croissante", traduisons "l"applicationfn"est pas positive" : "il existex2R;f(x)<0". Donc la négation de l"assertion complète est : " Il existex12Retx22Rtels quex1f(x2), ou il existex2R;f(x)<0". 4. Cette assertion se décompose de la manière sui vante: "(Il e xistex2R+) (f(x)60)". La négation de la
première partie est : "(pour toutx2R+)", et celle de la seconde est :"(f(x)>0)". Donc la négation de
l"assertion complète est : "Pour toutx2R+,f(x)>0".quotesdbs_dbs29.pdfusesText_35
4.8M12F18M22F29e2]0;+¥[M1M2 Quand elles sont fausses, donner leur négation. Nier la proposition: "tous les habitants de la rue du Havre qui ont les yeux bleus gagneront au loto et prendront
leur retraite avant 50 ans". Nier les assertions suivantes :
1 1.tout triangle rectangle possède un angle droit ;
2. dans toutes les écuries, tous les che vauxsont noirs ; 3. pour tout entier x, il existe un entierytel que, pour tout entierz, la relationz z4.8e>09a>0(jx7=5j Soientf;gdeux fonctions deRdansR. Traduire en termes de quantificateurs les expressions suivantes : 1.fest majorée;
2.fest bornée;
3.fest paire;
4.fest impaire;
5.fne s"annule jamais;
6.fest périodique;
7.fest croissante;
8.fest strictement décroissante;
9.fn"est pas la fonction nulle;
10.fn"a jamais les mêmes valeurs en deux points distincts;
11.fatteint toutes les valeurs deN;
12.fest inférieure àg;
13.fn"est pas inférieure àg.
Soitfune application deRdansR. Nier, de la manière la plus précise possible, les énoncés qui suivent :
1. Pour tout x2Rf(x)61.
2. L "applicationfest croissante.
3. L "applicationfest croissante et positive.
4. Il e xistex2R+tel quef(x)60.
5. Il e xistex2Rtel que quel que soity2R, sixf(y). On ne demande pas de démontrer quoi que ce soit, juste d"écrire le contraire d"un énoncé.
Montrer que
8e>09N2Ntel que(n>N)2e<2n+1n+2<2+e):
2 Ensembles
Exercice 9SoitA;Bdeux ensembles, montrer{(A[B) ={A\{Bet{(A\B) ={A[{B. Montrer par contraposition les assertions suivantes,Eétant un ensemble : 1.8A;B2P(E) (A\B=A[B))A=B,
2.8A;B;C2P(E) (A\B=A\CetA[B=A[C))B=C.
SoientEetFdeux ensembles,f:E!F. Démontrer que : 8A;B2P(E) (AB))(f(A)f(B)),
8A;B2P(E)f(A\B)f(A)\f(B),
8A;B2P(E)f(A[B) =f(A)[f(B),
8A;B2P(F)f1(A[B) =f1(A)[f1(B),
8A2P(F)f1(FnA) =Enf1(A).
Montrez que chacun des ensembles suivants est un intervalle que vous calculerez. I=+¥\
n=1 1n ;2+1n etJ=+¥[ n=2 1+1n ;n Exercice 13Soit(fn)n2Nune suite d"applications de l"ensembleNdans lui-même. On définit une applicationfdeNdans
Nen posantf(n) =fn(n)+1. Démontrer qu"il n"existe aucunp2Ntel quef=fp. 1. Soit p1;p2;:::;pr,rnombres premiers. Montrer que l"entierN=p1p2:::pr+1 n"est divisible par aucun des entierspi. 2. Utiliser la question précédente pour montrer par l"absurde qu"il e xisteune infinité de nombres premiers.
4 Récurrence
Exercice 15Montrer :
1. nå k=1k=n(n+1)2 8n2N: 2. nå k=1k2=n(n+1)(2n+1)6 8n2N: SoitXun ensemble. Pourf2F(X;X), on définitf0=idet par récurrence pourn2Nfn+1=fnf. 1. Montrer que 8n2Nfn+1=ffn.
2. Montrer que si fest bijective alors8n2N(f1)n= (fn)1. Soit la suite(xn)n2Ndéfinie parx0=4 etxn+1=2x2n3x n+2. 1. Montrer que : 8n2Nxn>3.
2. Montrer que : 8n2Nxn+13>32
(xn3). 3. Montrer que : 8n2Nxn>32
n+3. 4. La suite (xn)n2Nest-elle convergente ?
Indication pourl"exer cice2 NAttention : la négation d"une inégalité stricte est une inégalité large (et réciproquement).
Indication pour
l"exer cice 3 NFaire un dessin deF1et deF2. Essayer de voir si la difficulté pour réaliser les assertions vient dee"petit"
(c"est-à-dire proche de 0) ou dee"grand" (quand il tend vers+¥).Indication pourl"exer cice8 NEn fait, on a toujours :
2n+1n+262. Puis chercher une condition surnpour que l"inégalité
2e<2n+1n+2
soit vraie.Indication pourl"exer cice9 NIl est plus facile de raisonner en prenant un élémentx2E. Par exemple, soitF;Gdes sous-ensembles deE.
Montrer queFGrevient à montrer que pour toutx2Falorsx2G. Et montrerF=Gest équivalent àx2F si et seulement six2G, et ce pour toutxdeE. Remarque : pour montrerF=Gon peut aussi montrerFG puisGF. Enfin, se rappeler quex2{Fsi et seulement six=2F.Indication pourl"exer cice13 NPar l"absurde, supposer qu"il existep2Ntel quef=fp. Puis pour un telp, évaluerfetfpen une valeur bien
choisie.Indication pourl"exer cice14 NPour la première question vous pouvez raisonner par contraposition ou par l"absurde.
Indication pour
l"exer cice 16 NPour les deux questions, travailler par récurrence.
Indication pour
l"exer cice 17 N1.Récurrence : calculer xn+13.
2. Calculer xn+1332
(xn3). 3. Récurrence. 5
Correction del"exer cice1 N1.(
2., 3.)Correction del"exer cice2 N1.(a) est f ausse.C arsa nég ationqui est 8x2R9y2Rx+y60 est vraie. Étant donnéx2Ril existe
toujours uny2Rtel quex+y60, par exemple on peut prendrey=(x+1)et alorsx+y=xx1= 160.
2. (b) est vraie, pour un xdonné, on peut prendre (par exemple)y=x+1 et alorsx+y=1>0. La négation de (b) est9x2R8y2Rx+y60. 3. (c) : 8x2R8y2Rx+y>0 est fausse, par exemplex=1,y=0. La négation est9x2R9y2 Rx+y60.
4. (d) est vraie, on peut prendre x=1. La négation est:8x2R9y2Ry26x.Correction del"exer cice3 N1.Cette proposition est vraie. En ef fetsoit e>0, définissonsM1= (2e
;0)2F1etM2= (2e ;e2 )2F2, alors M 1M2=e2
0 la proposition est donc démontrée. 2. Soit deux points fixés M1,M2vérifiant cette proposition, la distanced=M1M2est aussi petite que l"on
veut donc elle est nulle, doncM1=M2; or les ensemblesF1etF2sont disjoints. Donc la proposition est fausse. La négation de cette proposition est : 8M12F18M22F29e2]0;+¥[M1M2>e
et cela exprime le fait que les ensemblesF1etF2sont disjoints. 3. Celle ci est ég alementf ausse,en ef fetsupposons qu"elle soit vraie, soit alors ecorrespondant à cette
proposition. SoitM1= (e+2;0)etM2= (1;1), on aM1M2>e+1 ce qui est absurde. La négation est : 8e2]0;+¥[9M12F19M22F2M1M2>e
C"est-à-dire que l"on peut trouver deux points aussi éloignés l"un de l"autre que l"on veut.
4. Cette proposition est vraie, il suf fitde choisir e=M1M2+1. Elle signifie que la distance entre deux points donnés est un nombre fini !Correction del"exer cice4 N"Il existe un habitant de la rue du Havre qui a les yeux bleus, qui ne gagnera pas au loto ou qui prendra sa
retraite après 50 ans."Correction del"exer cice5 N1."Il e xisteun triangle rectangle qui n"a pas d"angle droit." Bien sûr cette dernière phrase est f ausse!
2. "Il e xisteune écurie dans laquelle il y a (au moins) un che valdont la couleur n"est pas noire." 6 3.Sachant que la proposition en lang agemathématique s"écrit
8x2Z9y2Z8z2Z(z la négation est 9x2Z8y2Z9z2Z(zx+1):
4.9e>08a>0(jx7=5je):Correction del"exer cice6 N1.9M2R8x2Rf(x)6M;
2.9M2R9m2R8x2Rm6f(x)6M;
3.8x2Rf(x) =f(x);
4.8x2Rf(x) =f(x);
5.8x2Rf(x)6=0;
6.9a2R8x2Rf(x+a) =f(x);
7.8(x;y)2R2(x6y)f(x)6f(y));
8.8(x;y)2R2(xf(y));
9.9x2Rf(x)6=0;
10.8(x;y)2R2(x6=y)f(x)6=f(y));
11.8n2N9x2Rf(x) =n;
12.8x2Rf(x)6g(x);
13.9x2Rf(x)>g(x).Correction del"exer cice7 NDans ce corrigé, nous donnons une justification, ce qui n"était pas demandé.
1. Cette assertion se décompose de la manière sui vante: ( Pour tout x2R) (f(x)61). La négation de "(
Pour toutx2R)" est "Il existex2R" et la négation de "(f(x)61)" estf(x)>1. Donc la négation de l"assertion complète est : "Il existex2R;f(x)>1". 2. Rappelons comment se traduit l"assertion "L "applicationfest croissante" : "pour tout couple de réels
(x1;x2), six16x2alorsf(x1)6f(x2)". Cela se décompose en : "(pour tout couple de réelsx1etx2) (x16x2impliquef(x1)6f(x2))". La négation de la première partie est : "(il existe un couple de réels
(x1;x2))" et la négation de la deuxième partie est : "(x16x2etf(x1)>f(x2))". Donc la négation de
l"assertion complète est : "Il existex12Retx22Rtels quex16x2etf(x1)>f(x2)". 3. La négationest:"l"application fn"estpascroissanteoun"estpaspositive". Onadéjàtraduit"l"application
fn"est pas croissante", traduisons "l"applicationfn"est pas positive" : "il existex2R;f(x)<0". Donc la négation de l"assertion complète est : " Il existex12Retx22Rtels quex1f(x2), ou il existex2R;f(x)<0". 4. Cette assertion se décompose de la manière sui vante: "(Il e xistex2R+) (f(x)60)". La négation de la
première partie est : "(pour toutx2R+)", et celle de la seconde est :"(f(x)>0)". Donc la négation de
l"assertion complète est : "Pour toutx2R+,f(x)>0".quotesdbs_dbs29.pdfusesText_35
Nier la proposition: "tous les habitants de la rue du Havre qui ont les yeux bleus gagneront au loto et prendront
leur retraite avant 50 ans".Nier les assertions suivantes :
11.tout triangle rectangle possède un angle droit ;
2. dans toutes les écuries, tous les che vauxsont noirs ; 3.pour tout entier x, il existe un entierytel que, pour tout entierz, la relationz Soitfune application deRdansR. Nier, de la manière la plus précise possible, les énoncés qui suivent : On ne demande pas de démontrer quoi que ce soit, juste d"écrire le contraire d"un énoncé. Exercice 13Soit(fn)n2Nune suite d"applications de l"ensembleNdans lui-même. On définit une applicationfdeNdans Utiliser la question précédente pour montrer par l"absurde qu"il e xisteune infinité de nombres premiers. Indication pourl"exer cice2 NAttention : la négation d"une inégalité stricte est une inégalité large (et réciproquement). (c"est-à-dire proche de 0) ou dee"grand" (quand il tend vers+¥).Indication pourl"exer cice8 NEn fait, on a toujours : soit vraie.Indication pourl"exer cice9 NIl est plus facile de raisonner en prenant un élémentx2E. Par exemple, soitF;Gdes sous-ensembles deE. Enfin, se rappeler quex2{Fsi et seulement six=2F.Indication pourl"exer cice13 NPar l"absurde, supposer qu"il existep2Ntel quef=fp. Puis pour un telp, évaluerfetfpen une valeur bien choisie.Indication pourl"exer cice14 NPour la première question vous pouvez raisonner par contraposition ou par l"absurde. (d) est vraie, on peut prendre x=1. La négation est:8x2R9y2Ry26x.Correction del"exer cice3 N1.Cette proposition est vraie. En ef fetsoit e>0, définissonsM1= (2e Soit deux points fixés M1,M2vérifiant cette proposition, la distanced=M1M2est aussi petite que l"on Celle ci est ég alementf ausse,en ef fetsupposons qu"elle soit vraie, soit alors ecorrespondant à cette C"est-à-dire que l"on peut trouver deux points aussi éloignés l"un de l"autre que l"on veut. points donnés est un nombre fini !Correction del"exer cice4 N"Il existe un habitant de la rue du Havre qui a les yeux bleus, qui ne gagnera pas au loto ou qui prendra sa retraite après 50 ans."Correction del"exer cice5 N1."Il e xisteun triangle rectangle qui n"a pas d"angle droit." Bien sûr cette dernière phrase est f ausse! Cette assertion se décompose de la manière sui vante: ( Pour tout x2R) (f(x)61). La négation de "( Rappelons comment se traduit l"assertion "L "applicationfest croissante" : "pour tout couple de réels (x16x2impliquef(x1)6f(x2))". La négation de la première partie est : "(il existe un couple de réels (x1;x2))" et la négation de la deuxième partie est : "(x16x2etf(x1)>f(x2))". Donc la négation de La négationest:"l"application fn"estpascroissanteoun"estpaspositive". Onadéjàtraduit"l"application Cette assertion se décompose de la manière sui vante: "(Il e xistex2R+) (f(x)60)". La négation de la première partie est : "(pour toutx2R+)", et celle de la seconde est :"(f(x)>0)". Donc la négation de1.fest majorée;
2.fest bornée;
3.fest paire;
4.fest impaire;
5.fne s"annule jamais;
6.fest périodique;
7.fest croissante;
8.fest strictement décroissante;
9.fn"est pas la fonction nulle;
10.fn"a jamais les mêmes valeurs en deux points distincts;
11.fatteint toutes les valeurs deN;
12.fest inférieure àg;
13.fn"est pas inférieure àg.
Pour tout x2Rf(x)61.
2. L "applicationfest croissante.
3. L "applicationfest croissante et positive.
4. Il e xistex2R+tel quef(x)60.
5. Il e xistex2Rtel que quel que soity2R, sixMontrer que
8e>09N2Ntel que(n>N)2e<2n+1n+2<2+e):
2 Ensembles
Exercice 9SoitA;Bdeux ensembles, montrer{(A[B) ={A\{Bet{(A\B) ={A[{B. Montrer par contraposition les assertions suivantes,Eétant un ensemble : 1.8A;B2P(E) (A\B=A[B))A=B,
2.8A;B;C2P(E) (A\B=A\CetA[B=A[C))B=C.
SoientEetFdeux ensembles,f:E!F. Démontrer que : 8A;B2P(E) (AB))(f(A)f(B)),
8A;B2P(E)f(A\B)f(A)\f(B),
8A;B2P(E)f(A[B) =f(A)[f(B),
8A;B2P(F)f1(A[B) =f1(A)[f1(B),
8A2P(F)f1(FnA) =Enf1(A).
Montrez que chacun des ensembles suivants est un intervalle que vous calculerez. I=+¥\
n=1 1n ;2+1n etJ=+¥[ n=2 1+1n ;n 4 Récurrence
Exercice 15Montrer :
1. nå k=1k=n(n+1)2 8n2N: 2. nå k=1k2=n(n+1)(2n+1)6 8n2N: SoitXun ensemble. Pourf2F(X;X), on définitf0=idet par récurrence pourn2Nfn+1=fnf. 1. Montrer que 8n2Nfn+1=ffn.
2. Montrer que si fest bijective alors8n2N(f1)n= (fn)1. Soit la suite(xn)n2Ndéfinie parx0=4 etxn+1=2x2n3x n+2. 1. Montrer que : 8n2Nxn>3.
2. Montrer que : 8n2Nxn+13>32
(xn3). 3. Montrer que : 8n2Nxn>32
n+3. 4. La suite (xn)n2Nest-elle convergente ?
Indication pour
l"exer cice 3 NFaire un dessin deF1et deF2. Essayer de voir si la difficulté pour réaliser les assertions vient dee"petit"
2n+1n+262. Puis chercher une condition surnpour que l"inégalité
2e<2n+1n+2
Indication pour
l"exer cice 16 NPour les deux questions, travailler par récurrence.
Indication pour
l"exer cice 17 N1.Récurrence : calculer xn+13.
2. Calculer xn+1332
(xn3). 3. Récurrence. 5
Correction del"exer cice1 N1.(
2., 3.)Correction del"exer cice2 N1.(a) est f ausse.C arsa nég ationqui est 8x2R9y2Rx+y60 est vraie. Étant donnéx2Ril existe
toujours uny2Rtel quex+y60, par exemple on peut prendrey=(x+1)et alorsx+y=xx1= 160.
2. (b) est vraie, pour un xdonné, on peut prendre (par exemple)y=x+1 et alorsx+y=1>0. La négation de (b) est9x2R8y2Rx+y60. 3. (c) : 8x2R8y2Rx+y>0 est fausse, par exemplex=1,y=0. La négation est9x2R9y2 Rx+y60.
4. 1M2=e2
8M12F18M22F29e2]0;+¥[M1M2>e
et cela exprime le fait que les ensemblesF1etF2sont disjoints. 3. 8e2]0;+¥[9M12F19M22F2M1M2>e
3.Sachant que la proposition en lang agemathématique s"écrit
8x2Z9y2Z8z2Z(z
9x2Z8y2Z9z2Z(z
4.9e>08a>0(jx7=5j
2.9M2R9m2R8x2Rm6f(x)6M;
3.8x2Rf(x) =f(x);
4.8x2Rf(x) =f(x);
5.8x2Rf(x)6=0;
6.9a2R8x2Rf(x+a) =f(x);
7.8(x;y)2R2(x6y)f(x)6f(y));
8.8(x;y)2R2(x
9.9x2Rf(x)6=0;
10.8(x;y)2R2(x6=y)f(x)6=f(y));
11.8n2N9x2Rf(x) =n;
12.8x2Rf(x)6g(x);
13.9x2Rf(x)>g(x).Correction del"exer cice7 NDans ce corrigé, nous donnons une justification, ce qui n"était pas demandé.
1.
[PDF] salaire apprenti bp
[PDF] salaire apprenti coiffure 2017
[PDF] salaire apprenti bp coiffure
[PDF] salaire bp coiffure 2017
[PDF] salaire bp coiffure
[PDF] remuneration apprenti metallurgie 2016
[PDF] salaire apprenti convention metallurgie
[PDF] salaire apprenti métallurgie 2017
[PDF] clause de propriété intellectuelle exemple
[PDF] exemple de contrat renouvelable par tacite reconduction
[PDF] contrat d'apprentissage pour les plus de 26 ans
[PDF] contrat d'apprentissage pour les plus de 30 ans
[PDF] contrat d'apprentissage plus de 26 ans dérogation
[PDF] contrat de professionnalisation pour les plus de 30 ans
