[PDF] Système de coordonnées Pour convertir des cartésiennes

View - Download Système de coordonnées

Previous PDF

Next PDF

Coordonnées

COORDONÉES POLAIRES (rappel)

En géométrie plane, le système

de coordonnées polaires est utilisé pour donner une description plus simple de certaines courbes (et surfaces).

La figure nous permet de nous

Souvenir de la relation entre coordonnées polaires et cartésiennes. ƒSi le point Pa (x, y) pour coordonnées cartésiennes et (r, ș)comme coordonnées polaires alors x= rcos șy = r sin ș r2= x2+ y2tan ș= y/x

COORDONNÉES CYLINDRIQUES

En dimension 3 il y a un système de coordonnées, appelé coordonnées cylindriques, qui :

ƒEst similaire aux coordonnées polaires.

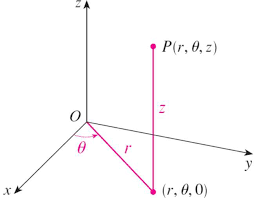
ƒDonne une description simple de nombreux domaines (surfaces, volumes). Dans le système de coordonnées cylindriques, un point Pde -D) est représenté

Par le triplet (r, ș, z), où :

ret șsontles coordonnées polairesdelaprojection de P sur le plan xy, zestla distance orientéedu plan xyàP.

Pour convertir des coordonnées cylindriques en

cartésiennes, on utilise : x= rcos ș y= rsin ș z= z Pour convertir des cartésiennes en cylindriques, on utilise: r2= x2+ y2 tan ș= y/x z = z

COORDONNÉES CYLINDRIQUES

Exemple

a.Placer le point de coordonnéescylindriques(2, 2ʌ/3, 1)et donner sescoordonnéesrectangulaires. b.Donner les coordonnéescylindriquesdu point de coordonnéesrectangulaires(3, 3, 7).

Solution

a) Le point de cylindriquescoordonnées (2, 2ʌ/3, 1)estplacésur la figure.

Sescoordonnéesrectangulairessont

Le point a doncpour coordonnéesrectangulaires(1, , 1). 3

212cos 2 132

232sin 2 332

1 x y z S

Solution (b)

On a :

Un jeude coordonnéescylindriquesestdonc:

Un autre:

ƒCommepour les coordonnéespolaires, ily a uneinfinite de choixpossibles.

223 ( 3) 3 2

37tan 1, so 234

7 r n z T T S (3 2,7 /4, 7)(3 2, /4, 7)

Coordonnéescylindriques

Les coordonnéescylindriquessontutilesdansles problèmes oùexisteunesymétrieaxiale. On choisitalorsdes z de façonà cecoincide avec cetaxe de symétrie. ƒPar exemple, pour le cylindreà base circulaire, z, ila pour équationcartésiennex2+ y2= c2. ƒEncoordonnéescylindriques, cecylindrea comme

équation: r= c(beaucoup plus simple!).

Exercice

z= ren coordonnées cylindriques

Solution

ƒz de la surface) est la même que r(distance de ce point à z).

ƒComme ș

z. Donc, toute section horizontale de la surface par un plan z= k (k> 0) est a cercle de rayon k. Ceci suggère que la surface est coordonnées rectangulaires.

On a : z2= r2= x2+ y2, cette équation

(z2= x2+ y2équation cartésienne z.

SYSTÈME DE COORDONNÉES SPHERIQUES (3D)

Le systèmede coordonnéessphériquesestun autresystèmede coordonéesutile entroisdimensions. ƒIl simplifieenparticulierles calculstriples sur des volumes limitéspar des portions de sphèresoude cônes. Les coordonnéessphériques(ȡ, ș, ĭ) Pde sont:

ƒȡ= |OP|, ladistance deO

à P(ȡ0)

ƒș,le mêmeangle

coordonnéescylindriques.

ƒĭ, entre les vecteurszet

OP. l'angle formé par les vecteurs zet OPest appelé colatitude le plan équatorial et OP).

Notons que la première coordonnée (la

distance entre Oet P) est toujours positive, et que la colatitudeest comprise entre 0 et ,

En physique, les notations șet ĭsont

Généralement interverties, comme sur la

figure ci-contre.

La distance est souvent notée r.

REMARQUE TRÈS IMPORTANTE

Notations "physiques»

Notations "mathématiques»

COORDONNÉES SPHÈRIQUES

Utiliser un système de coordonnées sphériques peut être particulièrement utile pour résoudre des problèmes présentant origine du système. ca alors une équation très simple :

ȡ= c.

Our= c en

Le grapheéquationș= c

(= c ennotations physiques) estun demi plan verticalcontenant Oz.

équationĭ= c(ș= c en

notations physiques) représenteun demi-cône z.

COORDONNÉES SPHÈRIQUES

La relation entre coordonnéescartésiennesand sphériquesse déduitde la figure.

COORDONNÉES SPHÈRIQUES & CARTÉSIENNES

Considéronslestriangles OPQ

et, ona: z= ȡcos ĭ, r= ȡsin ĭ

ƒEt comme,

x= rcos ș, y= rsin ș

On obtientles formulesde

conversion : x= ȡsin ĭcos ș y= ȡsin ĭsin ș z= ȡcos ĭ

Avec les notations physiques, la relation

de passage aux coordonnées cartésiennes s'écritdonc :

COORDONNÉES SPHÈRIQUES & CARTÉSIENNES

Exercice :

Le point (r= 2, = ʋ/3, = ʋ/4) est donné en coordonnées schéma et calculer ses cordonnées cartésiennes.

Solution

Coordonnéescartésiennes:

1 2

3 1 3sin cos 2sin cos 23 4 2 22

3 1 3sin sin 2sin sin 23 4 2 22

cos 2cos 2 13 x x z U I T

SSU I T

SUI x y z

La formuledonnantla distance indiqueque :

r2= x2+ y2 + z2 ƒOnutilise cetteéquation pourconvertirles coordonnées cartésiennes en coordonnéesspheriques. Exercice: Le point estdonnéencoordonnées cartésiennes. Caculerdes coordonnéessphériquespour cepoint.

0,2 3, 2

COORDONNÉES SPHÈRIQUES & CARTÉSIENNES

On a :

Doncon a : r = 4, ߠ

ଷ(colatitude), ߮

Solution

Considérons M de coordonnées

sphériques (r, , ).

Le vecteur position de Mest :

OM= rur

urest le vecteur unitaire radial.

Repèrecomobile

Les coordonnées cartésiennes de Msont :

On aura donc pour ur: •‹ߠ...‘•߮ǡ•‹ߠ•‹߮ǡ...‘•ߠ

Repèrecomobile

Lvarie le point M

décrit un cercle, dans un plan parallèle à (Oxy), de rayon ݎ...‘•ߠ

Le vecteur unitaire tangent en Mà

cette courbe est noté u, il est situé dans le plan "horizontal» (x,y).

OM(et donc

à ur), puisque la norme de OMest constante

lorsque Mse déplace sur le cercle. on a : u= -sinux+ cosuy

Repèrecomobile

varie le point

Mdécrit un demi grand cercle

(méridien).

Le vecteur unitaire tangent à

cette courbe, en M, est noté u. Il est orthogonal à urpuisque, lorsque Mdécrit le demi cercle, la norme du vecteur OMest constante (ۻ۽ uest dans le plan "méridien», il est donc orthogonal à uqui est dans un plan "horizontal». Le repère comobile(M,ur,u,u) est orthonormé direct et lié à M. cartésiennes de u(à vérifier en exercice) : (coscos, cossin, -sin)

Exercice

Donner les équations paramétriques de la courbe décrite par le point Mde coordonnées sphériques (r, , ) lorsque varie (ret restant fixés). Calculer, par dérivation, le vecteur tangent à la courbe, en déduire les coordonnées cartésiennes de u Donner les équations paramétriques de la courbe décrite par le point Mde coordonnées sphériques (r, , ) lorsque varie (retquotesdbs_dbs6.pdfusesText_12

[PDF] coordonnées sphériques cartésiennes

[PDF] coordonnées d'une personne

[PDF] coordonnées vecteur

[PDF] coordonnées personnelles

[PDF] coordonnées lambert

[PDF] coordonnés

[PDF] coordonnées cylindriques pdf

[PDF] coordonnées cylindriques cours

[PDF] repère cartésien orthonormé

[PDF] repère x y

[PDF] coordonnées x y z

[PDF] repérage d'un point dans l'espace

[PDF] lire les coordonnées d'un point dans l'espace

[PDF] coordonnées d'un point géométrie dans l'espace

[PDF] lire les coordonnées d'un point dans un repère quelconque