 Système de coordonnées
Système de coordonnées
Pour convertir des cartésiennes en cylindriques on utilise: r2 = x2 + y2 tan θ La relation entre coordonnées cartésiennes and sphériques se déduit de la ...
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
 Les systèmes de coordonnées.
Les systèmes de coordonnées.
4 sept. 2023 ... systèmes de coordonnées qui figurent explicitement à votre programme : cartésiennes cylindriques
 lestransformations du système de coordonnées - effets sur les
lestransformations du système de coordonnées - effets sur les
une symétrie sphérique et même cylindrique
 Syst`emes de coordonnées
Syst`emes de coordonnées
cartésiennes et cylindriques sont liées par. : x = ρ cosφ y = ρ sin φ z = z. M ... En coordonnées sphériques un point M(r) est considéré comme un point d'une ...
 Les différents systèmes de coordonnées
Les différents systèmes de coordonnées
Coordonnées cartésiennes : x y
 Systèmes de coordonnées Repères locaux
Systèmes de coordonnées Repères locaux
systèmes de coordonnées cylindriques et coordonnées sphériques. Mais ce n coordonnées cartésiennes polaires
 Systèmes de coordonnées Repères locaux
Systèmes de coordonnées Repères locaux
coordonnées cartésiennes polaires
 TD no 1. Outils mathématiques
TD no 1. Outils mathématiques
Coordonnées cartésiennes cylindriques
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
 Système de coordonnées
Système de coordonnées
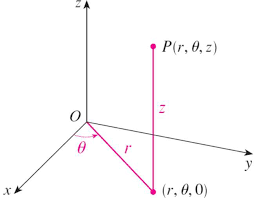
Dans le système de coordonnées cylindriques un point P de l'espace (3-D) est représenté La relation entre coordonnées cartésiennes and sphériques se.
 Transformation coordonnées
Transformation coordonnées
La raison est que ce système planétaire a une symétrie sphérique et même cylindrique
 Chapter 1 - Syst`emes de coordonnées
Chapter 1 - Syst`emes de coordonnées
1.1.1 Repérage d'un vecteur en coordonnées cylindriques pour un point donné les composantes cartésiennes et cylindriques sont liées par.
 Cinématique et dynamique du point matériel (Cours et exercices
Cinématique et dynamique du point matériel (Cours et exercices
Ensuite nous étudions les différents types de mouvement et les différents systèmes de coordonnées (cartésiennes
 TD no 1. Outils mathématiques
TD no 1. Outils mathématiques
Exercice I. Coordonnées cartésiennes cylindriques
 Systèmes de coordonnées
Systèmes de coordonnées
26 août 2020 Utiliser les systèmes de coordonnées cartésiennes cylindriques et sphériques. Exprimer à partir d'un schéma le déplacement élémentaire.
 MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
confondu avec celui des cartésiennes. • vecteur radial : Système. Cartésien. Cylindrique. Sphérique. Schéma. Coordonnées de M. (
 Polycopie PHYSIQUE 1
Polycopie PHYSIQUE 1
1- Vecteur position dans les systèmes de coordonnées (cartésiennes cylindriques
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 [PDF] Système de coordonnées
[PDF] Système de coordonnées
Pour convertir des coordonnées cylindriques en cartésiennes on utilise : x = r cos ? y = r sin ? z = z Pour convertir des cartésiennes en cylindriques on
 [PDF] COORDONNÉES CARTÉSIENNES CYLINDRIQUES SPHÉRIQUES
[PDF] COORDONNÉES CARTÉSIENNES CYLINDRIQUES SPHÉRIQUES
On utilisera les coordonnées cylindriques dès que la distance à l'axe Oz joue un rôle important dans l'exercice Page 2 ? Systèmes de coordonnées (35-500)
 [PDF] [PDF] Les systèmes de coordonnées - Physique
[PDF] [PDF] Les systèmes de coordonnées - Physique
3 sept 2022 · devez savoir sur les trois systèmes de coordonnées qui figurent explicitement à votre programme: cartésiennes cylindriques sphériques
 [PDF] Transformation coordonnées
[PDF] Transformation coordonnées
La raison est que ce système planétaire a une symétrie sphérique et même cylindrique alors que le système de coordonnées cartésiennes a une symétrie
 [PDF] Syst`emes de coordonnées
[PDF] Syst`emes de coordonnées
1 1 1 Repérage d'un vecteur en coordonnées cylindriques On se rappelle qu'en coordonnées cartésiennes le vecteur position s'écrit
 [PDF] Les différents systèmes de coordonnées
[PDF] Les différents systèmes de coordonnées
Coordonnées cartésiennes : x y z Coordonnées cylindriques : ? ? z Attention les angles ? des coordonnées cylindriques et sphériques sont
 (PDF) Coordonnées cylindriques et sphériques zakaria housni
(PDF) Coordonnées cylindriques et sphériques zakaria housni
Un tel système se prête naturellement à l'usage des coordonnées sphériques pour exprimer de façon simple le mouvement de la bille dans la glissière
 [PDF] Systèmes de coordonnées - Fun MOOC
[PDF] Systèmes de coordonnées - Fun MOOC
Coordonnées curvilignes d'un point de l'espace M point de coordonnées cartésiennes (xyz) dans R3 muni d'un repère (0ijk) Autre système de coordonnées
 Les coordonnées cartésiennes cylindriques et sphériques
Les coordonnées cartésiennes cylindriques et sphériques
Les coordonnées cylindriques correspondent aux coordonnées polaires mais en rajoutant l'axe z qui est le même qu'en coordonnées cartésiennes : Le repère en
Comment passer des coordonnées cartésiennes aux coordonnées cylindriques ?
Les coordonnées cylindriques sont utiles dans les problèmes où existe une symétrie axiale. On choisit alors l'axe des z de façon à ce qu'il coincide avec cet axe de symétrie. Par exemple, pour le cylindre à base circulaire, d'axe z, il a pour équation cartésienne x2 + y2 = c2.Comment déterminer les coordonnées cylindrique ?
On appelle coordonnées sphériques divers systèmes de coordonnées orthogonales de l'espace analogues aux coordonnées polaires du plan. Un point de l'espace est repéré dans ces systèmes par la distance à une origine (le pôle) et par deux angles.Quels sont les coordonnées sphériques ?
Un système de coordonnées cartésiennes permet de déterminer la position d'un point dans un espace affine (droite, plan, espace de dimension 3, etc.) muni d'un repère cartésien. Le mot cartésien vient du mathématicien et philosophe fran?is René Descartes.
 1
1 Chapter 1
Syst`emes de coordonn´ees
1.1 Rep`ere cart´esien
Un rep`ere cart´esien est d´efini par un point origineOet trois axes (Ox,Oy,Oz) perpendiculaires
entre eux. Les vecteurs unitaires port´es par les axes sont: ?ex,?ey,?ez. (voir figure 1.1a)) M"O z x y Mez ey ex r M"O z M ez eyex A( )M a)b) y xFigure 1.1:
On doit bien noter la disposition relative des directions (Ox,Oy,Oz). Telles qu"elles sontplac´ees, elles d´efinissent un tri`edre direct. Dans un teltri`edre, un bonhomme transperc´e des pieds
`a la tˆete parOy, regardant la directionOz, a la directionOx`a sa gauche. On peut noter aussi que
Ox,Oy,etOzsont respectivement orient´es selon les directions du pouce, de l"index et du majeurde la main droite. Un pointMde l"espace est rep´er´e par les trois composantes du vecteur-→r
joignantO`aM(-→r=--→OM) (voir fig. 1.1a) : r(x,y,z) =x?ex+y?ey+z?ez M ?est la projection deMdans le plan (x0y). Les composantesxetyde-→rsont les coordonn´ees du pointM?dans ce plan. La composantezest obtenue en tra¸cant la parall`ele `aOM?passant par M. On dira indistinctement qu"un objet se trouve au pointMou en-→r.1.1.1 Rep´erage d"un vecteur en coordonn´ees cylindriques
Quand il s"agit de rep´ererun vecteur
-→A(M) dont le point d"application est situ´e au pointM(x,y,z),ou-→r(x,y,z), on peut d´ecrire ce vecteur avec le mˆeme base de vecteurs unitaires?ex,?ey,?ez(voir
fig.1.1b)). Nous appelons donc ?ex,?ey,?ez, un r´ep`ere orthonorm´eglobalparce qu"on peut l"utiliser `a d´ecrire un vecteur ayant n"importe lequel point d"application.1.2. COORDONN´EES CYLINDRIQUES2
1.2 Coordonn´ees cylindriques
1.2.1 Rep´erage d"un point en coordonn´ees cylindriques
En coordonn´ees cylindriques, un pointMde l"espace est rep´er´e comme un point de cylindre (droit,
`a base circulaire) dont l"axeOzest g´en´eralement confondu avec l"axeOzdu rep`ere cart´esien.
Le pointM(ou-→r) est rep´er´e par
•le rayonρdu cylindre sur lequel il s"appuie •zsa cote par rapport au plan de r´ef´erencexOy •φl"angle (Ox,OM?) o`uM?est la projection deMsur le planxOy.La notation
-→r(ρ,φ,z) vient se substituer `a-→r(x,y,z) du rep`ere cart´esien. Vous pouvez facile-
ment v´erifier que, pour un point donn´e, les composantes cart´esiennes et cylindriques sont li´ees par
x=ρcosφ y=ρsinφ z=z M" ?O z x y M e? ez e?Figure 1.2:
1.2.2 Rep´erage d"un vecteur en coordonn´ees cylindriques
Nous nous posons la question de rep´erer un vecteur dont le point d"application est situ´e au point
M(ρ,φ,z), ou-→r(ρ,φ,z). Pour cela nous attachons `aMun rep`ere orthonorm´e local (?eρ,?eφ,?ez).
Nous l"appelonslocalparce qu"il n"est pas le mˆeme pour tous les pointsMde l"espace. Ce rep`ere local est fait de 3 vecteurs unitaires de base orthogonaux ( ?eρ,?eφ,?ez) : ?eρ(ou?uρou?ρ) est un vecteur parall`ele `a---→OM?. ?eφ(ou?uφou?φ) est parall`ele au vecteur tangent enM?au cercle de rayonOM?contenu dans le planxOy ?ez(ou?uzou?z) est parall`ele `a l"axeOz Dans ce rep`ere, le vecteur champ ´electrique a 3 composantes et s"´ecrit E(M) =Eρ?eρ+Eφ?eφ+Ez?ezou-→E(M) =(( E E E z))1.2. COORDONN´EES CYLINDRIQUES3
Au pointM, la relation entre les vecteurs unitaires (?eρ,?eφ,?ez) et les vecteurs unitaires cart´esiennes
?ex,?ey,?ez) s"´ecrivent : eρ= cosφ?ex+ sinφ?ey eφ=-sinφ?ex+ cosφ?ey ez=?ez(1.1) On peut voir cette relation comme une relation matricielle (tensorielle) (?eρ eφ ez)) cosφsinφ0 -sinφcosφ00 0 1))
(?ex ey ez)) =T((?ex ey ez)) Les relation inverses sont obtenues en prenant l"inverse dela matriceT. Puisque les deux bases sont orthonorm´ees, on aT-1=Tto`uTtest la transpose de la matriceT. On obtient de cette mani`ere les vecteurs unitaires ( ?ex,?ey,?ez) en fonction des (?eρ,?eφ,?ez) : (?ex ey ez)) cosφ-sinφ0 sinφcosφ00 0 1))
(?eρ eφ ez)) c"est-`a-dire. ex= cosφ?eρ-sinφ?eφ ey= sinφ?eρ+ cosφ?eφ ez=?ez On peut ´egalement v´erifier ces relations avec de la g´eom´etrie.1.2.3 Position et d´eplacement (diff´erentielle) en coordonn´ees cylindriques
On se rappelle qu"en coordonn´ees cart´esiennes, le vecteur position s"´ecritOM=x?ex+y?ey+z?ez
et la diff´erentielle de cette position s"´ecrit dOM≡∂--→OM
En coordonn´ees cylindriques par contre, on ´ecritOM=ρ?eρ+z?ez
et la diff´erentielle s"exprime : dOM=∂--→OM
Si l"on veut exprimerd--→OMen coordonn´ees cylindriques, il faut tenir compte du fait que le vecteur
unitaire local ?eρd´epend de la coordonn´eeφ(voir eq.(1.1)) : OM OM∂φ=ρ∂?eρ∂φ=ρ∂∂φ(cosφ?ex+ sinφ?ey) =ρ(-sinφ?ex+ cosφ?ey) =ρ?eφ
Un d´eplacement en coordonn´ees cylindriques s"exprime donc1.3. COORDONN´EES SPH´ERIQUES4
Cette formule est tr`es utile afin d"en d´eduire des volumes et des surfaces ´el´ementaires. Par exemple,
un ´el´ement de volume ´el´ementaire en coordonn´ees cylindriques s"exprime dV= (dρ)(ρdφ)(dz) =ρdρdφdz(1.3) Exemple :On peut utiliser ce r´esultat `a d´eriver la formule pour un cylindre de rayonRet de coteL:Volume
cylindreR,L=??? cylindre dV=? R 0 dρ? 2π 0ρdφ?
L 0 dz=L? R 0ρdρ?
2π 0 dφ = 2πL? R 0ρdρ=πR2L
1.2.4 Gradient en coordonn´ees cylindriques
La diff´erentielle en coordonn´ees cylindriques d"un champscalaire Φ s"exprime : dΦ =∂Φ Le gradient en coordonn´ees cylindriques est d´efinie telleque : dΦ =---→gradΦ·d--→OM(1.5) Une comparaison entre (1.2), (1.4) et (1.5) montre que l"expression du gradient en coordonn´ees cylindriques s"´ecrit : gradΦ =∂Φ Exemple : Lorsque le potentiel ´electriqueV(M) est exprim´e en coordonn´ees cylindriques(ρ,θ,z), les composantes du champ ´electrique dans le rep`ere cylindrique attach´e au pointMsont
donn´ees par:-→E(ρ,φ,z) =----→gradV(ρ,φ,z)E=Eρ?eρ+Eφ?eφ+Ez?ezE
ρ=-∂V
Eφ=-1
ρ∂V∂ρ
E z=-∂V ∂zLe potentiel cr´e´e par une distribution lin´eique de charge avec une densit´e par unit´e de longueur
λest donn´e parV(ρ) =-λ
2π?0ln(ρ) +Cte. On obtient imm´ediatement le champ ´electrique par
E(ρ) =----→gradV(ρ) =λ
2π?0ρ?eρ
1.3 Coordonn´ees sph´eriques
1.3.1 Rep´erage d"un point en coordonn´ees sph´eriques
En coordonn´ees sph´eriques, un pointM(r) est consid´er´e comme un point d"une sph`ere centr´ee sur
O. Le pointMest rep´er´e
•par le rayonrde la sph`ere `a laquelle il appartient •L"angleθentre la direction-→Ozet la direction--→OM.θ= (-→Oz,--→OM)•l"angleφentre la direction-→Oxet la direction---→OM?o`uM?est la projection deMdans le
planxOy.:φ= (-→Ox,---→OM?)1.3. COORDONN´EES SPH´ERIQUES5
M" ?O z x y r M e ere? M""Figure 1.3:Coordonn´ees sph´eriques
Un pointM(r) ´etant donn´e, on trouve que ses coordonn´ees cart´esiennes s"´ecrivent en fonction
des coordonn´ees sph´eriques; ainsi: x=rsinθcosφ y=rsinθsinφ z=rcosθEn g´eographie, o`u on est amen´e `a rep´erer un point sur la sph`ere terrestre, l"angleθindiquerait
la latitude par rapport au pˆole nord et l"angleφ, la longitude est par rapport au m´eridien de
r´ef´erence.1.3.2 Rep´erage d"un vecteur en coordonn´ees sph´eriques
En coordonn´ees sph´eriques, un vecteur-→E(M) (ou simplement-→E(-→r)) attach´e au pointM(r) est
rep´er´e par trois composantes (Er,Eθ,Eφ) dans un rep`ere orthonorm´elocal(?er,?eθ,?eφ) :
E(M) =Er?er+Eθ?eθ+Eφ?eφ
avec ?er(ou?urou?r) est un vecteur parall`ele `a--→OM. ?eθ(ou?uθou?θ) est parall`ele au vecteur tangent enMau cercle de rayonrd´ecrit dans le plan qui contient `a la fois les directions-→Oz,--→OMetOM?. ?eφ(ou?uφou?φ) est tangent enMau cercle de centreM??et de rayonM??M=OM?, contenu dans le plan perpendiculaire `a-→Oz. Au pointM, la relation entre les vecteurs unitaires (?er,?eθ,?eφ) et les vecteurs unitairesquotesdbs_dbs30.pdfusesText_36[PDF] coordonnées d'une personne
[PDF] coordonnées vecteur
[PDF] coordonnées personnelles
[PDF] coordonnées lambert
[PDF] coordonnés
[PDF] coordonnées cylindriques pdf
[PDF] coordonnées cylindriques cours
[PDF] repère cartésien orthonormé
[PDF] repère x y
[PDF] coordonnées x y z
[PDF] repérage d'un point dans l'espace
[PDF] lire les coordonnées d'un point dans l'espace
[PDF] coordonnées d'un point géométrie dans l'espace
[PDF] lire les coordonnées d'un point dans un repère quelconque
