[PDF] CHAPITRE 26 ANALYSE VECTORIELLE 26.1 Opérateurs de l

View - Download CHAPITRE 26 ANALYSE VECTORIELLE 26.1 Opérateurs de l

Previous PDF

Next PDF

CHAPITRE26ANALYSE VECTORIELLE

L"analyse vectorielle fait intervenir à la fois des outils analytiques (dérivées partielles) et du calcul vectoriel. Les notions de base de l"analyse vectorielle sont indispensables en électrostatique, en électromagnétisme, en mécanique des ‡uides. Après avoir étudié ce chapitre, vous devez : A.Connaître les opérateurs de l"analyse vectorielle (nabla, gradient, diver- gence et rotationnel) et savoir démontrer leurs propriétés. B.Savoir calculer des intégrales de surface simples. C.Connaître la dé...nition du ‡ux d"un champ de vecteurs à travers une surface orientée, et savoir calculer des ‡ux simples. D.Savoir ce qu"est un champ à ‡ux conservatif. E.Connaître les formules de Stokes et d"Ostrogradski.

F.Savoir ce qu"est un angle solide.

26.1 Opérateurs de l"analyse vectorielle

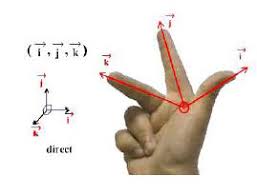
L"espace est rapporté à la base orthonormée directe(!i ;!j ;!k):On dé...nit l"opérateur aux dérivées partiellesnablapar r=@@x !i+@@y !j+@@z !k :(26.1) On notera quenablaest unopérateur aux dérivées partielles, et pas un vec- teur. Il opèreà gaucheen utilisant les trois types de multiplication vectorielle. Par exemple, soit d"abordU=U(M)une fonction de trois variables (fonc-

304 Chapitre 26 : Analyse vectorielle

tion scalaire). On dé...nit legradientdeUpar gradU=!rU=@@x !i+@@y !j+@@z !k

U=@U@x

!i+@U@y !j+@U@z !k :

On retrouve (23.13). Si

!E=!E(M) =Ex!i+Ey!j+Ez!kun champ de vecteurs, on dé...nit ladivergencede!Epar div !E=!r:!E=0 B

BB@@@x

@@y @@z 1 C CCA:0 @E x E y E z1 A =@Ex@x +@Ey@y +@Ez@z ;(26.2) et lerotationnelde!Epar rot!E=!r ^!E=0 B

BB@@@x

@@y @@z 1 C CCA^0 @E x E y E z1 A (26.3) @Ez@y @Ey@z !i@Ez@x @Ex@z !j+@Ey@x @Ex@y !k : Remarque 26.1L"opérateur nabla est essentiellement unenotation, très commode pour retenir les dé...nitions du gradient, de la divergence et du rotationnel. On notera que!gradUet!rot!Esont desvecteursdeR3;alors que div!Eest un nombre réel, c"est-à-dire unscalaire. Exemple 26.1Soitkun paramètre. Considérons lechamp newtoniendé...ni en coordonnées sphériques [voir(23:17)] par!E=!E(M) =kr 2!er:

Puisquer=

!OM et!er=!OM !OM ;on a

E=k!OM

!OM

3=k(x2+y2+z2)32

x!i+y!j+z!k :(26.4)

Il en résulte que

div !E=k@@x xx2+y2+z232 +@@y yx2+y2+z232 @@z zx2+y2+z232

Chapitre 26 : Analyse vectorielle 305

En utilisant la formule qui donne la dérivée d"un produit, il vient @@x xx2+y2+z232 =x2+y2+z232

3x2x2+y2+z252

x2+y2+z252 x2+y2+z23x2 x2+y2+z252

2x2+y2+z2:

Les dérivées partielles par rapport àyetzs"obtiennent sans calcul en per- mutant les rôles dexetyet ceux dexetzrespectivement. Ainsi div = 0: Un champ newtonien est à divergence nulle.Un calcul analogue montre qu"on a aussi!rot!E=!0(exercice 26.1). Remarque 26.2.Composons la divergence et le gradient : div !gradU = div@U@x !i+@U@y !j+@U@z !k @@x @U@x +@@y @U@y +@@z @U@z =@2U@x

2+@2U@y

2+@2U@z

2: On introduit ainsi un nouvel opérateur, lelaplacien:

U= div(!gradU) =!r2U=@2U@x

2+@2U@y

2+@2U@z

2:(26.5)

A partir des dé...nitions, on peut démontrer desformules d"analyse vectorielle. Les deux plus importantes, qui doivent être connues, sont rot(!gradU) =!0;div(!rot!E) = 0:(26.6) Voir l"exercice 26.2 pour leur démonstration. Les exercices 26.3 et 26.4 donnent d"autres exemples de formules utiles.

26.2 Surfaces de l"espace

26.2.1 Représentation d"une surface

Dans l"espace rapporté au repère orthonormé direct(O;!i ;!j ;!k);unesur- face()est dé...nie par une équation de la formeF(x;y;z) = 0:Par exemple, l"équationax+by+cz+d= 0est celle d"un plan, tandis que l"équation

306 Chapitre 26 : Analyse vectorielle

(xx )2+ (yy )2+ (zz )2=R2est celle de la sphère de centre de rayonR:Un troisième exemple important est le suivant. Exemple 26.2Soienta; b; c2R+:L"équation cartésienne x 2a 2+y2b 2+z2c

2= 1(26.7)

est celle d"unellipsoïdede centreO;d"axes principauxOx; Oy; Oz:Pour visualiser cette surface, coupons-la par un plan horizontal d"équationz=z0; avecc < z0< c:La section correspondante a pour équation x 2a 2+y2b

2= 1z20c

2,x2 aq1z20c 2 2+y2 bq1z20c 2 2= 1: Il s"agit donc d"une ellipse. Ainsi la section d"un ellipsoïde par un plan hori- zontal est une ellipse. Il en est de même lorsqu"on coupe l"ellipsoïde par un planx=x0ouy=y0:Ainsi un ellipsoïde a la forme d"un ballon de rugby aplati, comme représenté ...gure 26.1. Sia=b=c=R;l"ellipsoïde est la sphère de centreOde rayonR:j M q ds

Figure 26.1Figure 26.2

x y zIl est souvent commode d"utiliser unereprésentation paramétriqued"une sur- face. Puisqu"une surface est un objet à deux dimensions, il est nécessaire d"utiliser deux paramètres. Ainsi une représentation paramétrique d"une sur- face est de la formex=f(u;v),y=g(u;v),z=h(u;v):On parle alors de nappe paramétrée. Exemple 26.3La surface de la sphère de centreOde rayonRpeut être paramétrée par x=Rsincos' ; y=Rsinsin' ; z=Rcos;(26.8) le paramétrage(26:8)n"est pas autre chose que les formules de passage des

Chapitre 26 : Analyse vectorielle 307

coordonnées sphériques aux coordonnées cartésiennes, avecr=R(formules (5.21)), puisque le pointMse déplace à la surface de la sphère.

26.2.2 Vecteur normal à une surface

Théorème 26.1Un vecteur normal à la surface()d"équation cartésienne F(x;y;z) = 0au pointM(x;y;z)est le vecteur!N=!gradF(M): DémonstrationDéplaçons le pointMd"un déplacement in...nitésimal!dM en restant sur la surface()(...gure 26.3). AlorsFreste égal à0dans ce dé- placement, de telle sorte quedF= 0:OrdF=!gradF(M):!dM:Il en résulte

que!gradF(M):!dM= 0pour tout déplacement!dMsur();c"est-à-dire que!gradF(M)et!dMsont orthogonaux pour tout déplacement in...nitésimal sur

la surface de()à partir deM:Ainsi!gradF(M)est bien normal à()au pointM:SM

Figure 26.3Figure 26.4SMgradf(M)

dM n2n

1Exemple 26.4Si(P)est le plan d"équationax+by+cz+d= 0;un vecteur

normal à(P)est !N=!gradF=@Fdx !i+@F@y !j+@F@z !k=a!i+b!j+c!k : Le vecteur normal est indépendant deMet on retrouve le théorème 9.2. Exemple 26.5SoitM(x;y;z)un point de l"ellipsoïde d"équation carté- sienne x2a 2+y2b 2+z2c

2= 1. Un vecteur normal enMest

N=!gradF=@Fdx

!i+@F@y !j+@F@z !k= 2xa

2!i+yb

2!j+zc

2!k Dans le cas particulier de la sphère de centreOde rayonR;on voit que N=2R 2 x!i+y!j+z!k =2R 2!OM:

On retrouve ainsi que le rayon

!OMest orthogonal à la surface de la sphère, ce qui est évident géométriquement.

308 Chapitre 26 : Analyse vectorielle

Remarque 26.3Soit!Nun vecteur normal en un pointMd"une surface ():On peut dé...nir deux vecteurs normauxunitairesenM(...gure 26.4) : n1=!N !N et!n2=!N !N =!n1: Lorsqu"on a choisi un des deux vecteurs normaux unitaires, on dit qu"on a orientéla surface():Ceci revient à dé...nir unsens positif de traverséede ()(dans le sens du vecteur normal unitaire!nchoisi). Remarque 26.4On dit qu"une surface de l"espace estferméelorsqu"elle délimite un intérieur et un extérieur. Par exemple une sphère ou un ellipsoïde sont des surfaces fermées. Par contre un plan n"en est pas une. Par convention, une surface fermée est toujours orientée vers l"extérieur, c"est-à-dire que son vecteur normal unitaire est dirigé vers l"extérieur. Ainsi la sphère de centre Ode rayonRest orientée par le vecteur normal unitaire n=!OM !OM =1R x!i+y!j+z!k

26.2.3 Lignes de champs et surfaces équipotentielles

Soit !Eun champ de vecteurs. On appelleligne de champtoute courbe(L) telle que, en tout pointMde(L);le champ!EenMest tangent à(L).

Par exemple, si

!E=g!kest le champ de pesanteur au voisinage du sol, les lignes de champ sont les droites verticales (...gure 26.5). Si!E=kr

2!erest

un champ newtonien d"origineO;les lignes de champ sont les droites passant parO(...gure 26.6).Figure 26.5Figure 26.6ggggg EEE

EESupposons maintenant que le champ

!Edérive d"un potentiel scalaireV; alors!E=!gradV:On appellesurface équipotentielletoute surface où les points sont au même potentiel, c"est-à-dire d"équationV=C;oùCest une constante donnée.

Chapitre 26 : Analyse vectorielle 317

Ainsi,le ‡ux du champ newtonien!E=kr

2!erà travers()vaut=k

Montrons que la formule (26.17) généralise la dé...nition géométrique lorsque la droiteOMcoupe()en un seul pointMpour tout pointMde()(...gure

26.18). La surface ferméeABCDA0B0C0D0est alors un tube de champ pour

le champ newtonien!E1=1r

2!er;puisque le champ est tangent à chacune

des surfaces latéralesABB0A0; BCC0B0; CDD0C0etDAA0D0:Le champ newtonien étant à ‡ux conservatif (exemple 26.15), le ‡ux entrant est égal au ‡ux sortant, qui est, par (26.17), l"angle solide :En notantSla surface A

0B0C0D0sur la sphère de centreOde rayon1;nous avons donc

ZZ S1r

2!er:!n:d=ZZ

S d=S;

puisque au pointNsitué à la surface de la sphère, on ar= 1et!er=!n:L"angle solide dé...ni par Gauss comme le ‡ux d"un champ newtonien

généralise bien la dé...nition géométrique. Théorème 26.4L"angle solide sous lequel on voit une surface fermée() depuis un pointOde l"espace vaut4si le pointMest intérieur à();et

0si le pointOest extérieur à():

DémonstrationSi on regarde()depuis un point intérieur, on est com- plètement entouré par elle. L"angle solide correspond donc à tout l"espace, c"est-à-dire4sr. Si on regarde la surface depuis un point extérieur, le ‡ux de!E1à travers()est nul, car!E1est à ‡ux conservatif dans():

Exercices du chapitre 26

Les basiques

Exercice 26.1 (A)Calculer!rot!E;où!E=kr

2!erest un champ newtonien.

Exercice 26.2 (A)Démontrer que!rot(!gradU) =!0etdiv(!rot!E) = 0:

Exercice 26.3 (A)Soit=(M)une fonction scalaire,!E=!E(M)et!F=!F(M)des champs de vecteurs. Démontrer les formules suivantes :

1)div(!E) =!E:!grad+div!E:

2)div(!E^!F) =!F :!rot!E!E:!rot!F :

Exercice 26.4 (A)Transformer!u=!rot(!E)et!v=!rot(!rot!E):

318 Chapitre 26 : Analyse vectorielle

Exercice 26.5 (A)Soit!!un vecteur constant, et soit!V=!!^!OM:

Démontrer que!!=12

!rot!V : Exercice 26.6 (B)Calculer l"intégrale de surfaceI=RR

Sf(M)d;où

f(M) =f(x;y;z) =pz:IciR >0est ...xé, etSest la demi-sphère d"équation x

2+y2+z2=R2; z0;

Exercice 26.7 (B)SoitR >0eta >0et soitSest le cylindre d"équation x

2+y2=R2;0za:Calculer l"intégrale de surfaceI=RR

Sf(M)d;où

f(M) =f(x;y;z) =zx 2+y2: Exercice 26.8 (C)SoitR >0eth >0:Soit la portionde cylindre d"équationx2+y2=R2;0zh; x0; y0:Déterminer le ‡ux du champ de vecteurs!E=z!i+x!j3y2z!kà travers(on précisera l"orientation choisie). Exercice 26.9 (A,C,E)SoitR >0;et soitSla demi-sphère d"équation z0; x2+y2+z2=R2:Soit!E=y!i+x(12z)!jxy!k :

1) Calculer!rot!E:En déduire le ‡ux de!rot!Eà traversS(on précisera

l"orientation choisie).

2) Retrouver ce résultat en utilisant la formule de Stokes.

3) Retrouver ce résultat en fermant la surfaceSpar le disque de centreOde

rayonRsitué dans le planOxy;et en utilisant la formule d"Ostrogradski. Exercice 26.10 (C,D,E)SoitR >0donné, et soitSla demi-sphère d"équa- tionx2+y2+z2=R2; z0:En utilisant la formule d"Ostrogradski, trouver le ‡ux du champ constant!E=E!kà traversS(on précisera l"orientation deSchoisie). Exercice 26.11 (C,D,F)SoitR >0eta >0:SoitDle disque de la ...gure

26.19, centré surOyet perpendiculaire àOy:

1) Calculer l"angle solide sous lequel on voit ce disque depuis le pointO:

2) Calculer le ‡ux du champ newtonien!E=kr

2!erà traversD;orienté dans

le sens desycroissants.H ab

Figure26.19Figure26.20h

SMR axz y DO

Chapitre 26 : Analyse vectorielle 319

Les techniques

Exercice 26.12On se propose de calculer le ‡ux du champ de vecteurs!E=xy2!ià travers la surface de la sphère(S)de centreOde rayonR

1)Calcul direct.

a) Calculer les intégralesI=R2

0sin2'cos2'd'etJ=R

0sin5d:

b) Calculer!E:!n, puis le ‡uxdu champ!Eà travers(S):

2)Calcul par la formule d"Ostrogradski.

Calculerdiv!E;en déduire:

Exercice 26.13Déterminer le moment d"inertie d"une sphère creuse homo- gène, de rayonR;de masse totaleM;de masse surfacique;par rapport à un axe()passant par son centre.

Les exotiques et les olympiques

Exercice 26.14Soitle rectangle0xa;0yb(...gure 26.20). Soit

H(0;0;h);avech >0:

1) Calculer

@@y h yh2+x2+y212 i

2) Montrer que l"angle solide

suivant lequel on voitdu pointHvaut =hbZ x=a x=0dx(h2+x2)ph

2+b2+x2:

3) Calculer

grâce au changement de variablex=ph

2+b2tant:

Solutions des exercices du module 3 817

(donc par unhyperplandeR4):Soitxla section correspondante. Il est clair quex a pour équationy2+z2+t2=R2x2:Il s"agit donc d"une sphère dans l"espace à trois dimensionsOyzt;de rayon=pR

2x2:L"intégrale quadruple qui donne l"hyper-

volume s"écrit doncV=Rx=R x=R RRR xdydzdt dx:Or l"intégrale triple correspond au volume (ordinaire) intérieur à la sphèrex:Donc

V=Rx=R

x=R43

3dx=43

Rx=R x=R pR

2x23dx=83

Rx=R x=0 pR

2x23dx:

On peut calculer cette intégrale grâce au changement de variablex=Rsin:Il vient V=83 R4R2

0cos4d:Cette dernière intégrale se calcule par linéarisation :

cos 4=116 ei+ei4=116 e4i+ 4e2i+ 6 + 4e2i+e4i 18 (cos4+ 4cos2+ 3):

Il vient ...nalementV=12

2R4:

Solutions des exercices du chapitre 26

Exercice 26.1On a!E=k!OM

!OM

3=kx2+y2+z232

(x!i+y!j+z!k);d"où rot!E=!r ^!E=0 B

BBB@@@x

@@y @@z 1 C

CCCA^0

B @xx2+y2+z232 y x2+y2+z232 z x2+y2+z232 1 C A 0 B BBB@z @@y h x2+y2+z232 i y@@z h x2+y2+z232 i x @@z h x2+y2+z232 i z@@x h x2+y2+z232 i y @@x h x2+y2+z232 i x@@y h x2+y2+z232 i1quotesdbs_dbs15.pdfusesText_21

[PDF] livre d anglais 1am algerie 2016

[PDF] sujet danglais de 2eme année lycée langue

[PDF] anglais 1as scientifique

[PDF] cours 1ere année anglais lmd

[PDF] bts industriels exemples dossiers ccf anglais

[PDF] expression oral anglais bts

[PDF] vocabulaire anglais administratif

[PDF] anglais des affaires cours gratuits

[PDF] english business communication pdf

[PDF] cours d'anglais 1ere année universitaire st

[PDF] la phonétique et la phonologie pdf

[PDF] cours de phonétique française

[PDF] cours de phonétique française s1 pdf

[PDF] exercice phonétique français pdf

[PDF] tableau phonétique français