 Paris 7 Agreg. interne – EXERCICES DANALYSE VECTORIELLE
Paris 7 Agreg. interne – EXERCICES DANALYSE VECTORIELLE
EXERCICES D'ANALYSE VECTORIELLE. Alain Laverne. 01 44 27 79 81 laverne@paris7 Le “truc” de Feynman (Le cours de physique
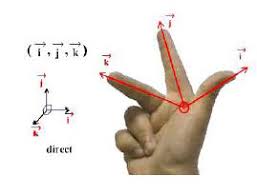 Chapitre 2 : Analyse vectorielle et systèmes de Coordonnées MI
Chapitre 2 : Analyse vectorielle et systèmes de Coordonnées MI
En physique on utilise deux types de grandeurs : les grandeurs scalaires et les Corrigés des exercices. Exercice 1. On a 1. ⃗⃗⃗⃗= ⃗+3 ⃗− 2 ⃗⃗ 2. ⃗⃗⃗⃗ ...
 TD 0 Analyse vectorielle — Rappels et compléments Exercice 0.1
TD 0 Analyse vectorielle — Rappels et compléments Exercice 0.1
Les exercices ne seront pas discutés en cours mais un corrigé sera mis à votre disposition en ligne. (http://www.ipcms.unistra.fr/?page_id=12803). Il est
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
e2ix = 1. Correction ▽. Vidéo □. [000108]. Exercice 6. Dans R2 on définit les Physique P 1995. Les matrices (. 0 1 1 0. 0 0 1 0. 0 0 0 0. 0 0 0 0 ) et (0 0 ...
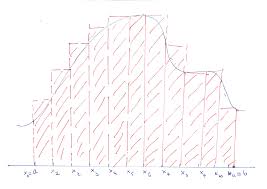 LM256 : Analyse vectorielle intégrales multiples
LM256 : Analyse vectorielle intégrales multiples
En guise d'exercice voyons maintenant comment les quantités physiques sont transportées Corrigé de l'examen du 5 Juin 2012. Exercice I. 1) on a. −−−→.
 Rappels de cours et exercices corrigés
Rappels de cours et exercices corrigés
28 nov. 2016 Chapitre 9 • Analyse vectorielle. 250. – –. –. 7.2 Divergence rotationnel ... En physique la façon d'écrire un nombre possède une signification ...
 Cours et Exercices de mécanique du point matériel
Cours et Exercices de mécanique du point matériel
d'analyse vectorielle écrit par Josiah Willard Gibbs pour ses étudiants en physique. [4] https://www.exoco-lmd.com/mecanique-du-point/exercices-corriges-de- ...
 ANALYSE MATRICIELLE ET ALGÈBRE LINÉAIRE APPLIQUÉE
ANALYSE MATRICIELLE ET ALGÈBRE LINÉAIRE APPLIQUÉE
Il aborda des problèmes difficiles en physique avec le Traité de dynamique Exercice 1.— Soit E un K-espace vectoriel. Montrer que pour tout vecteur x ...
 CHAPITRE 26 ANALYSE VECTORIELLE 26.1 Opérateurs de l
CHAPITRE 26 ANALYSE VECTORIELLE 26.1 Opérateurs de l
Un champ newtonien est à divergence nulle. Un calcul analogue montre qu'on a aussi −→ rot −→E = −→0 (exercice 26.1).
 Cours et Exercices dElectromagnétisme et Ondes pour les Master
Cours et Exercices dElectromagnétisme et Ondes pour les Master
➢ Chapitre 1 : Rappel d'analyse vectorielle. ➢ Chapitre 2 : Electrostatique exercices corrigés de Physique Dunod
 Rappels de cours et exercices corrigés
Rappels de cours et exercices corrigés
Nov 28 2016 Rappels de cours et exercices corrigés ... Chapitre 9 • Analyse vectorielle ... généralement
 Cours de Calcul Tensoriel avec Exercices corrigés
Cours de Calcul Tensoriel avec Exercices corrigés
3.1.4 Définition du produit tensoriel de deux espaces vectoriels . . . 62 5.1.2 Problèmes fondamentaux de l'analyse tensorielle . . . . . . . . 130.
 ANALYSE VECTORIELLE SEMAINE 3 - CORRECTION DES
ANALYSE VECTORIELLE SEMAINE 3 - CORRECTION DES
ANALYSE VECTORIELLE. SEMAINE 3. - CORRECTION DES EXERCICES 2 - 1.1 Exercice détaillé sur document principal. 1.2 Exercice avec indications et réponses.
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
229 245.00 Analyse vectorielle : forme différentielle champ de vecteurs
 Cours et Exercices dElectromagnétisme et Ondes pour les Master
Cours et Exercices dElectromagnétisme et Ondes pour les Master
Il est présenté sous forme de cours détaillé avec des exercices corrigés et d'autres proposés à résoudre. Chapitre 1 : Rappel d'analyse vectorielle.
 LM256 : Analyse vectorielle intégrales multiples
LM256 : Analyse vectorielle intégrales multiples
En guise d'exercice voyons maintenant comment les quantités physiques sont transportées par le champ de vecteurs. Soit f une quantité scalaire physique que
 Cinématique et dynamique du point matériel (Cours et exercices
Cinématique et dynamique du point matériel (Cours et exercices
La première partie est consacrée à un rappel mathématique sur l'analyse vectorielle qui est nécessaire pour exprimer les lois physiques.
 Espaces vectoriels
Espaces vectoriels
L'ensemble est-il un sous espace vectoriel de ?. 4 ? Si oui en donner une base. Allez à : Correction exercice 5. Exercice 6. Dans l'espace ?.
 ANALYSE MATRICIELLE ET ALGÈBRE LINÉAIRE APPLIQUÉE
ANALYSE MATRICIELLE ET ALGÈBRE LINÉAIRE APPLIQUÉE
ANALYSE MATRICIELLE. ET ALGÈBRE LINÉAIRE. APPLIQUÉE. - Notes de cours et de travaux dirigés -. PHILIPPE MALBOS malbos@math.univ-lyon1.fr
 Paris 7 Agreg. interne – EXERCICES DANALYSE VECTORIELLE
Paris 7 Agreg. interne – EXERCICES DANALYSE VECTORIELLE
EXERCICES D'ANALYSE VECTORIELLE. Alain Laverne Le “truc” de Feynman (Le cours de physique t. II
 Analyse Vectorielle : Cours et Exercices Corrigés - DZuniv
Analyse Vectorielle : Cours et Exercices Corrigés - DZuniv
Télécharger gratuitement le document Analyse Vectorielle : Cours et Exercices Corrigés en Cours - Analyse S1 sur DZuniv
 Analyse vectorielle - Exercices de cours - Unisciel
Analyse vectorielle - Exercices de cours - Unisciel
Exercice 1 1 · Exercice 1 2 · Exercice 1 3 · Exercice 1 4 · Exercice 1 5 · Exercice 1 6 · Exercice 1 7 · Exercice1 8 · Exercice 1 9 Propriétés du laplacien
 [PDF] Rappels de cours et exercices corrigés - Dunod
[PDF] Rappels de cours et exercices corrigés - Dunod
28 nov 2016 · Rappels de cours et exercices corrigés Chapitre 9 • Analyse vectorielle généralement en physique à une intensité)
 [PDF] LM256 : Analyse vectorielle intégrales multiples
[PDF] LM256 : Analyse vectorielle intégrales multiples
Dans ce chapitre nous rappelons quelques éléments de l'analyse des fonctions d'une variable réelle 1 1 Généralités sur les applications et les fonctions
 Examen corrige Analyse vectorielle exercices et corrigés
Examen corrige Analyse vectorielle exercices et corrigés
Analyse vectorielle - Cours examens et exercices gratuits et corrigés Le vecteur v (M) est dit fonction vectorielle de point ou champ vectoriel si
 [PDF] I-Analyse dimensionnelle et calcul vectoriel -Exercices corrigés
[PDF] I-Analyse dimensionnelle et calcul vectoriel -Exercices corrigés
Analyse dimensionnelle Exercice 1 1: Déterminez la dimension de l'énergie de la puissance du potentiel et de la résistance Exercice 1 2:
 [PDF] Éléments danalyse vectorielle - Mohamed Mebrouki
[PDF] Éléments danalyse vectorielle - Mohamed Mebrouki
Grandeur vectorielle : Grandeur physique complètement définie par sa longueur (module norme) sa direction (droite portant le vecteur) et son sens de parcourir
Cours de Calcul Tensoriel
avec Exercices corrigésTable des matières1 Les vecteurs6
1.1 Conventions d"écriture . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.1.1 Notation des vecteurs et de leurs composantes . . . . . . .. . 6
1.1.2 Convention de sommation . . . . . . . . . . . . . . . . . . . . 6
1.1.3 Sommation sur plusieurs indices . . . . . . . . . . . . . . . . . 7
1.1.4 Symbole de Kronecker . . . . . . . . . . . . . . . . . . . . . . 8
1.1.5 Symbole d"antisymétrie . . . . . . . . . . . . . . . . . . . . . . 8
1.2 Généralisation de la notion de vecteur . . . . . . . . . . . . . . .. . . 9
1.2.1 Exemple de vecteurs . . . . . . . . . . . . . . . . . . . . . . . 9
1.2.2 Propriétés des opérations sur les vecteurs . . . . . . . . .. . . 10
1.2.3 Autres exemples de vecteurs . . . . . . . . . . . . . . . . . . . 11
1.2.4 Définition générale des vecteurs . . . . . . . . . . . . . . . . . 12
1.2.5 Structure d"un ensemble . . . . . . . . . . . . . . . . . . . . . 12
1.3 Bases d"un espace vectoriel . . . . . . . . . . . . . . . . . . . . . . . .13
1.3.1 Exemples de vecteurs indépendants et dépendants . . . .. . . 13
1.3.2 Vecteurs de base . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3.3 Décomposition d"un vecteur sur une base . . . . . . . . . . . .14
1.3.4 Changement de base . . . . . . . . . . . . . . . . . . . . . . . 15
1.4 Produit scalaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4.1 Exemple de produits scalaires . . . . . . . . . . . . . . . . . . 16
1.4.2 Définition du produit scalaire . . . . . . . . . . . . . . . . . . 17
1.4.3 Expression générale du produit scalaire . . . . . . . . . . .. . 17
1.4.4 Vecteurs orthogonaux . . . . . . . . . . . . . . . . . . . . . . . 18
1.4.5 Bases orthogonales d"un espace vectoriel pré-euclidien . . . . . 18
1.4.6 Norme d"un vecteur . . . . . . . . . . . . . . . . . . . . . . . . 19
1.5 Espace vectoriel euclidien . . . . . . . . . . . . . . . . . . . . . . . .21
1.5.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.5.2 Bases orthonormées . . . . . . . . . . . . . . . . . . . . . . . . 21
1.5.3 Composantes contravariantes et covariantes . . . . . . .. . . 22
1.5.4 Expression du produit scalaire et de la norme . . . . . . . .. 24
1.5.5 Changement de base . . . . . . . . . . . . . . . . . . . . . . . 24
1.5.6 Bases réciproques . . . . . . . . . . . . . . . . . . . . . . . . . 25
1.5.7 Décomposition d"un vecteur sur les bases réciproques. . . . . 26
1.5.8 Produits scalaires des vecteurs de base . . . . . . . . . . . .. 27
1.6 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
12 Exemples de tenseurs euclidiens38
2.1 Changement de base . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.1.1 Composantes covariantes du tenseur fondamental . . . .. . . 38
2.1.2 Produit tensoriel de deux vecteurs . . . . . . . . . . . . . . . .40
2.2 Propriétés de changement de base . . . . . . . . . . . . . . . . . . . .42
2.2.1 Tenseur d"ordre deux . . . . . . . . . . . . . . . . . . . . . . . 42
2.2.2 Combinaisons linéaires de tenseurs . . . . . . . . . . . . . . .43
2.2.3 Tenseur d"ordre trois . . . . . . . . . . . . . . . . . . . . . . . 44
2.3 Exemples de tenseurs en Physique . . . . . . . . . . . . . . . . . . . .45
2.3.1 Tenseur d"inertie . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.3.2 Tenseur vitesse de rotation instantanée d"un solide .. . . . . . 46
2.3.3 Tenseurs des propriétés des milieux anisotropes . . . .. . . . 48
2.4 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
3 Algèbre tensorielle59
3.1 Tenseur d"ordre deux . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.1.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.1.2 Exemple de tenseur : produit tensoriel de triplets de nombres . 59
3.1.3 Propriétés du produit tensoriel . . . . . . . . . . . . . . . . . .61
3.1.4 Définition du produit tensoriel de deux espaces vectoriels . . . 62
3.1.5 Expression analytique du produit tensoriel de deux vecteurs . 63
3.1.6 Éléments d"un espace produit tensoriel . . . . . . . . . . . .. 64
3.1.7 Produit tensoriel de deux espaces vectoriels identiques . . . . 65
3.2 Tenseurs d"ordre quelconque . . . . . . . . . . . . . . . . . . . . . . .66
3.2.1 Produit tensoriel de plusieurs vecteurs . . . . . . . . . . .. . 66
3.2.2 Produit tensoriel d"espaces identiques . . . . . . . . . . .. . . 67
3.2.3 Classification des tenseurs . . . . . . . . . . . . . . . . . . . . 68
3.3 Produit scalaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.3.1 Produit scalaire d"un produit tensoriel par un vecteur de base 68
3.3.2 Produit scalaire d"un tenseur par un vecteur de base . .. . . 69
3.3.3 Produit scalaire de deux tenseurs de même ordre . . . . . .. 70
3.3.4 Composantes d"un tenseur pré-euclidien . . . . . . . . . . .. 70
3.3.5 Expression du produit scalaire . . . . . . . . . . . . . . . . . . 71
3.3.6 Tenseurs euclidiens d"ordre quelconque . . . . . . . . . . .. . 71
3.4 Bases d"un espace produit tensoriel . . . . . . . . . . . . . . . . .. . 72
3.4.1 Bases réciproques . . . . . . . . . . . . . . . . . . . . . . . . . 72
3.4.2 Composantes des tenseurs pré-euclidiens . . . . . . . . . .. . 73
3.4.3 Tenseurs d"ordre quelconque . . . . . . . . . . . . . . . . . . . 75
3.4.4 Changement de base . . . . . . . . . . . . . . . . . . . . . . . 76
3.4.5 Critère de tensorialité . . . . . . . . . . . . . . . . . . . . . . 78
3.5 Opérations sur les tenseurs . . . . . . . . . . . . . . . . . . . . . . . .79
3.5.1 Addition de tenseurs du même ordre . . . . . . . . . . . . . . 79
3.5.2 Multiplication tensorielle . . . . . . . . . . . . . . . . . . . . .79
3.5.3 Contraction des indices . . . . . . . . . . . . . . . . . . . . . . 79
3.5.4 Multiplication contractée . . . . . . . . . . . . . . . . . . . . . 81
3.5.5 Critères de tensorialité . . . . . . . . . . . . . . . . . . . . . . 82
23.6 Tenseurs particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
3.6.1 Tenseur symétrique . . . . . . . . . . . . . . . . . . . . . . . . 84
3.6.2 Quadrique représentative d"un tenseur symétrique . .. . . . . 84
3.6.3 Le tenseur fondamental . . . . . . . . . . . . . . . . . . . . . . 86
3.6.4 Tenseur antisymétrique . . . . . . . . . . . . . . . . . . . . . . 87
3.6.5 Produit extérieur de deux vecteurs . . . . . . . . . . . . . . . 88
3.7 Groupes ponctuels de symétrie . . . . . . . . . . . . . . . . . . . . . .89
3.7.1 Symétrie d"un cristal et de ses propriétés physiques .. . . . . 89
3.7.2 Effet de la symétrie sur les tenseurs . . . . . . . . . . . . . . . 90
3.8 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
4 Espaces ponctuels105
4.1 Espace ponctuel pré-euclidien . . . . . . . . . . . . . . . . . . . . .. 105
4.1.1 Exemple d"espace ponctuel . . . . . . . . . . . . . . . . . . . . 105
4.1.2 Définition d"un espace ponctuel . . . . . . . . . . . . . . . . . 106
4.1.3 Repères d"un espace ponctuel pré-euclidien . . . . . . . .. . . 107
4.1.4 Distance entre deux points . . . . . . . . . . . . . . . . . . . . 108
4.1.5 Dérivée d"un vecteur . . . . . . . . . . . . . . . . . . . . . . . 108
4.1.6 Notation des dérivées . . . . . . . . . . . . . . . . . . . . . . . 110
4.2 Coordonnées curvilignes . . . . . . . . . . . . . . . . . . . . . . . . . 110
4.2.1 Systèmes de coordonnées . . . . . . . . . . . . . . . . . . . . . 110
4.2.2 Coordonnées rectilignes . . . . . . . . . . . . . . . . . . . . . . 111
4.2.3 Coordonnées sphériques . . . . . . . . . . . . . . . . . . . . . 111
4.2.4 Coordonnées curvilignes . . . . . . . . . . . . . . . . . . . . . 112
4.3 Repère naturel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
4.3.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
4.3.2 Repère naturel en coordonnées sphériques . . . . . . . . . .. 113
4.3.3 Changement de coordonnées curvilignes . . . . . . . . . . . .. 114
4.3.4 Élément linéaire d"un espace ponctuel . . . . . . . . . . . . .. 115
4.4 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
5 Analyse tensorielle129
5.1 Symboles de Christoffel . . . . . . . . . . . . . . . . . . . . . . . . . . 129
5.1.1 Tenseurs sur un espace ponctuel . . . . . . . . . . . . . . . . . 129
5.1.2 Problèmes fondamentaux de l"analyse tensorielle . . .. . . . . 130
5.1.3 Symboles de Christoffel en coordonnées sphériques . . .. . . . 131
5.1.4 Définition des symboles de Christoffel . . . . . . . . . . . . . .132
5.1.5 Détermination des symboles de Christoffel . . . . . . . . . .. 133
5.1.6 Changement de base . . . . . . . . . . . . . . . . . . . . . . . 136
5.1.7 Vecteurs réciproques . . . . . . . . . . . . . . . . . . . . . . . 137
5.1.8 Équation des géodésiques . . . . . . . . . . . . . . . . . . . . . 137
5.2 Dérivée covariante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
5.2.1 Transport parallèle . . . . . . . . . . . . . . . . . . . . . . . . 139
5.2.2 Dérivée covariante d"un vecteur . . . . . . . . . . . . . . . . . 141
5.2.3 Dérivée covariante d"un tenseur . . . . . . . . . . . . . . . . . 143
5.2.4 Propriétés de la dérivée covariante d"un tenseur . . . .. . . . 144
35.2.5 Dérivée covariante seconde d"un vecteur . . . . . . . . . . .. 146
5.3 Différentielle absolue . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
5.3.1 Différentielle absolue d"un vecteur . . . . . . . . . . . . . . .. 146
5.3.2 Dérivée absolue le long d"une courbe . . . . . . . . . . . . . . 148
5.3.3 Différentielle absolue d"un tenseur . . . . . . . . . . . . . . .. 149
5.3.4 Théorème de Ricci . . . . . . . . . . . . . . . . . . . . . . . . 151
5.3.5 Symboles de Christoffel contractés . . . . . . . . . . . . . . . .151
5.4 Opérateurs différentiels . . . . . . . . . . . . . . . . . . . . . . . . . .152
5.4.1 Vecteur gradient . . . . . . . . . . . . . . . . . . . . . . . . . 152
5.4.2 Rotationnel d"un champ de vecteurs . . . . . . . . . . . . . . . 153
5.4.3 Divergence d"un champ de vecteurs . . . . . . . . . . . . . . . 153
5.4.4 Laplacien d"un champ de scalaires . . . . . . . . . . . . . . . . 154
5.5 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
6 Espaces de Riemann164
6.1 Exemples d"espace de Riemann . . . . . . . . . . . . . . . . . . . . . 164
6.1.1 Surfaces à deux dimensions . . . . . . . . . . . . . . . . . . . 164
6.1.2 Disque tournant . . . . . . . . . . . . . . . . . . . . . . . . . . 165
6.1.3 Espace de configuration . . . . . . . . . . . . . . . . . . . . . 166
6.2 Métrique riemannienne . . . . . . . . . . . . . . . . . . . . . . . . . . 167
6.2.1 Notion de variété . . . . . . . . . . . . . . . . . . . . . . . . . 167
6.2.2 Définition des espaces de Riemann . . . . . . . . . . . . . . . 168
6.2.3 Métrique euclidienne et riemannienne . . . . . . . . . . . . .. 169
6.2.4 Conditions nécessaires pour qu"une métrique soit euclidienne . 169
6.3 Propriétés géométriques . . . . . . . . . . . . . . . . . . . . . . . . . 170
6.3.1 Métrique euclidienne tangente en un point . . . . . . . . . .. 170
6.3.2 Propriétés géométriques déduites des métriques euclidiennes tangentes173
6.4 Propriétés différentielles . . . . . . . . . . . . . . . . . . . . . . . .. 174
6.4.1 Métrique euclidienne osculatrice . . . . . . . . . . . . . . . .. 174
6.4.2 Espace euclidien osculateur . . . . . . . . . . . . . . . . . . . 175
6.4.3 Différentielle absolue et dérivée covariante des tenseurs . . . . 176
6.4.4 Transport parallèle . . . . . . . . . . . . . . . . . . . . . . . . 177
6.4.5 Géodésiques d"un espace de Riemann . . . . . . . . . . . . . . 178
6.5 Déplacement le long d"une courbe . . . . . . . . . . . . . . . . . . . .179
6.5.1 Développement d"une courbe . . . . . . . . . . . . . . . . . . . 179
6.5.2 Déplacement associé à un cycle . . . . . . . . . . . . . . . . . 182
6.5.3 Expression du déplacement associé à un cycle . . . . . . . .. 185
6.6 Tenseur de Riemann-Christoffel . . . . . . . . . . . . . . . . . . . . .189
6.6.1 Détermination du tenseur de Riemann-Christoffel . . . .. . . 189
6.6.2 Composantes covariantes . . . . . . . . . . . . . . . . . . . . . 190
6.6.3 Système de coordonnées normales . . . . . . . . . . . . . . . . 190
6.6.4 Propriétés de symétrie . . . . . . . . . . . . . . . . . . . . . . 191
6.6.5 Première identité de Bianchi . . . . . . . . . . . . . . . . . . . 192
6.6.6 Composantes indépendantes . . . . . . . . . . . . . . . . . . . 192
6.7 Courbure Riemannienne . . . . . . . . . . . . . . . . . . . . . . . . . 193
6.7.1 Le tenseur de rotation en fonction du tenseur de Riemann-Christoffel193
46.7.2 Courbure riemannienne . . . . . . . . . . . . . . . . . . . . . . 1946.7.3 Tenseur de Ricci et courbure scalaire . . . . . . . . . . . . . .196
6.7.4 Seconde identité de Bianchi . . . . . . . . . . . . . . . . . . . 196
6.7.5 Tenseur d"Einstein . . . . . . . . . . . . . . . . . . . . . . . . 197
6.8 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
5Chapitre 1Les vecteurs1.1 Conventions d"écriture1.1.1 Notation des vecteurs et de leurs composantes
Les vecteurs et les tenseurs sont représentés par des lettres en caractère gras :x représentera par exemple un vecteur. Les composantes des vecteurs et des tenseurs sont notées par des lettresen italiqueavec des indices. Par exemple, un vecteurx de la géométrie classique, rapporté à une basee1,e2,e3, s"écrira : x=x1e1+x2e2+x3e3(1.1) Nous utiliserons également par la suite pour les composantes, des indices infé- rieurs (voir composantes covariantes et contravariantes).1.1.2 Convention de sommation
Lorqu"on effectue la somme de certaines quantités, on utilise couramment la lettre grecquesigmamajuscule pour représenter cette sommation. On a par exemple : x1y1+x2y2+.....+xnyn=n?
i=1x iyi(1.2) La convention de sommation d"Einstein va consister à utiliser le fait que l"indicerépété, ici l"indicei, va définir lui-même l"indication de la sommation. On écrit alors
avec cette convention : n i=1x iyi=xiyi(1.3) La variation de l"indice se fera sur tout le domaine possible, en général de 1 àn,sauf indication contraire. L"indice répété peut être affecté á des lettres différentes,
ou à une même lettre comme dans l"exemple suivant : A iixj=A11xj+A22xj+.....+Annxj(1.4) 6 Les indices peuvent être simultanément inférieurs ou supérieurs, ou l"un peutquotesdbs_dbs13.pdfusesText_19[PDF] sujet danglais de 2eme année lycée langue
[PDF] anglais 1as scientifique
[PDF] cours 1ere année anglais lmd
[PDF] bts industriels exemples dossiers ccf anglais
[PDF] expression oral anglais bts
[PDF] vocabulaire anglais administratif
[PDF] anglais des affaires cours gratuits
[PDF] english business communication pdf
[PDF] cours d'anglais 1ere année universitaire st
[PDF] la phonétique et la phonologie pdf
[PDF] cours de phonétique française
[PDF] cours de phonétique française s1 pdf
[PDF] exercice phonétique français pdf
[PDF] tableau phonétique français
