 I Module et Argument dun nombre complexe
I Module et Argument dun nombre complexe
Exemple 1 Calculer le module et l'argument de z1 =1+ i z2 =1+ i?3
 Calcul avec les nombres complexes/Module et argument
Calcul avec les nombres complexes/Module et argument
Calculer la distance où et sont les affixes des deux points. La distance AB est donc. 2)] Argument d'un nombre complexe non nul. Définition. Soit.
 Module et Argument dun nombre complexe
Module et Argument dun nombre complexe
Introduction : Les nombres complexes forment une extension de l'ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les
 Nombres complexes
Nombres complexes
On se place dans le plan complexe. nombre complexe z un vecteur dont : ... Calcul : pour z = a + jb on a.
 NOMBRES COMPLEXES (Partie 2)
NOMBRES COMPLEXES (Partie 2)
I. Module et argument d'un nombre complexe Propriétés : Soit z et z ' deux nombres complexes. ... Méthode : Calculer le module d'un nombre complexe.
 cours nombres complexes.pdf
cours nombres complexes.pdf
Question n°11 : Calculer le module du nombre imaginaire –7j. Question n°12 : Calculer le module du nombre réel – 393. 9-3- Argument.
 Nombres complexes
Nombres complexes
Exercice 15. Soit z un nombre complexe de module ? d'argument ?
 TP1 : Premiers pas en Maple
TP1 : Premiers pas en Maple
symboles représentant des nombres ou des objets mathématiques plus compliqués pour obtenir le nombre complexe conjugué le module et l'argument sont :.
 Forme trigonométrique dun nombre complexe – Applications
Forme trigonométrique dun nombre complexe – Applications
2.1 Argument d'un nombre complexe non nul . Remarques : Il découle facilement des règle de calcul sur les coordonnées de vecteurs que :.
 Module et Argument dun nombre complexe : règles de calcul.
Module et Argument dun nombre complexe : règles de calcul.
Module et Argument d'un nombre complexe : règles de calcul. Pour l'ensemble de cette fiche on suppose
 Nombres complexes EXOS CORRIGES - Meabilis
Nombres complexes EXOS CORRIGES - Meabilis
3) a) Placer dans le plan muni d’un repère orthonormal direct (Ou;;v) GG (unité graphique : 2 cm) les points : A d’affixe 2 B et C d’affixes respectives z1 et z2 et I milieu de [AB] b) Démontrer que le triangle OAB est isocèle JJ En déduire une mesure de l’angle (uO; I) GG c) Calculer l’affixe zI de I puis le module de zI
 Pascal Lainé - licence-mathuniv-lyon1fr
Pascal Lainé - licence-mathuniv-lyon1fr
Calculer le module et l'argument de chacun des nombres complexes suivants (en fonction de ????0) : =3 (2+ )(4+2 )(1+ )et =(4+2 )(?1+ ) (2? )3 Allez à : Correction exercice 1 : Exercice 2 : Mettre sous la forme + ?? (forme algébrique) les nombres complexes ????1= 3+6 3?4 ; ????2=(1+ 2? ) 2
 Searches related to calculer largument dun nombre complexe PDF
Searches related to calculer largument dun nombre complexe PDF
Nombres complexes – Fiche de cours 1 L’idée des nombres complexes Résoudre des équations polynomiales de degré n ?1 Exemple : obtenir 3 solutions pour l’équation x3+x+1=0 2 Ensemble des nombres complexes Il existe un ensemble noté ? tel que :- ??? (avec perte de la comparaison)- i?? tel que i2=?1 3 Nombre complexe
Comment calculer l'argument d'un complexe ?
Argument d'un complexe de module 1, définition géométrique par les rotations; un argument est défini modulo 2pi, et si |z|=1 alors un réel t est un argument de z ssi z=cos (t)+i.sin (t). Définition de l'argument d'un nombre complexe non nul: c'est l'argument de z/|z|.
Comment calculer l’argument d’un nombre complexe ?
Une autre méthode permettant de calculer l’argument d’un nombre complexe consiste à utiliser la trigonométrie des triangles rectangles pour calculer d’abord la mesure positive de l’angle aigu entre l’axe des réels et le segment reliant l’origine et l’image du nombre complexe dans le plan complexe.
Comment calculer le nombre complexe ?
Le nombre complexe z=blueD3+greenD4i z = 3+4i est sous forme algébrique. L'image dans le plan complexe du nombre complexe z=a+bi z = a+bi est le point M (a~;b) M (a ;b) :
Quels sont les nombres complexes?
Depuis le 16ème siècles, les mathématiciens ont eu besoin de nombres spéciaux, désormais connus comme nombres complexes. Le nombre complexe est un nombre de la forme a+bi, où a et b sont des — nombres réels, i — unité imaginaire qui est la solution de l'équation : i 2 =-1.
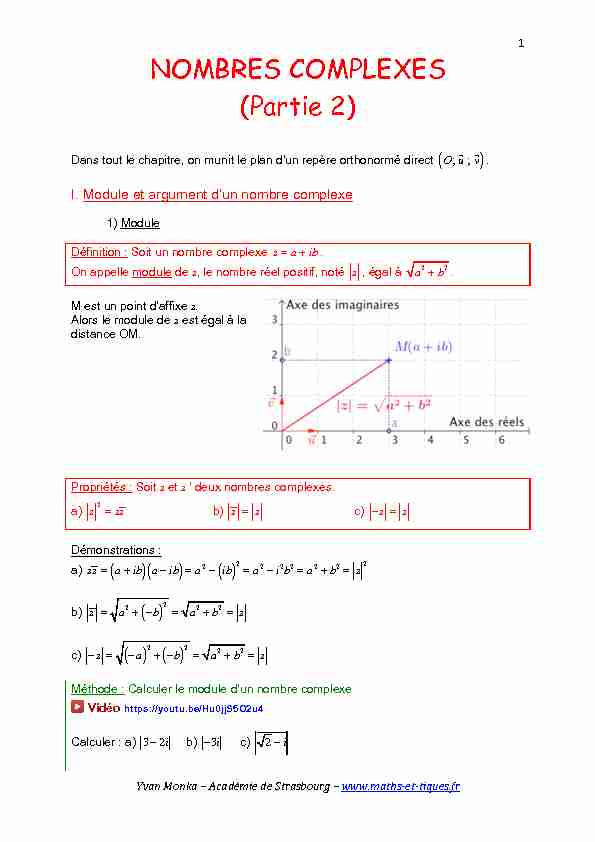
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr1NOMBRES COMPLEXES (Partie 2) Dans tout le chapitre, on munit le plan d'un repère orthonormé direct
O; u; v . I. Module et argument d'un nombre complexe 1) Module Définition : Soit un nombre complexe z=a+ib . On appelle module de z, le nombre réel positif, noté z , égal à a 2 +b 2. M est un point d'affixe z. Alors le module de z est égal à la distance OM. Propriétés : Soit z et z ' deux nombres complexes. a)
z 2 =zz b) z=z c) -z=zDémonstrations : a)
zz=a+ib a-ib =a 2 -ib 2 =a 2 -i 2 b 2 =a 2 +b 2 =z 2 b) z=a 2 +-b 2 =a 2 +b 2 =z c) -z=-a 2 +-b 2 =a 2 +b 2 =zMéthode : Calculer le module d'un nombre complexe Vidéo https://youtu.be/Hu0jjS5O2u4 Calculer : a) 3-2i
b) -3i c) 2-i YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr2a) 3-2i=3 2 +(-2) 2 =13 b) -3i=-3×i=3×1=3 c) 2-i=2-i=2 2 +-1 2 =2+1=32) Argument Définition : Soit un point M d'affixe z non nulle. On appelle argument de z, noté arg(z) une mesure, en radians, de l'angle
u;OM . Remarques : - Un nombre complexe non nul possède une infinité d'arguments de la forme arg(z)+2kπ k∈! . On notera arg(z) modulo 2π ou arg(z)2π - 0 n'a pas d'argument car dans ce cas l'angle u ;OM n'est pas défini. Exemple : Vidéo https://youtu.be/Hu0jjS5O2u4 Soit z=3+3i . Alors z=3+3i=3 2 +3 2 =18=32 Et arg(z)= 4 2π . Propriétés : Soit z un nombre complexe non nul. a) z est un nombre réel ⇔arg(z)=0π , b) z est un imaginaire pur ⇔arg(z)= 2 . c) arg(z)=-arg(z) d) arg(-z)=arg(z)+πYvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr3Démonstrations : a) Le point M d'affixe z appartient à l'axe des réels. b) Le point M d'affixe z appartient à l'axe des imaginaires. c) d) Ses résultats se déduisent par symétrie. II. Forme trigonométrique d'un nombre complexe 1) Définition Propriété : Soit
z=a+ib un nombre complexe non nul. On pose :θ=arg(z)
On a alors :
a=zcosθ et b=zsinθ . Définition : On appelle forme trigonométrique d'un nombre complexe z non nul l'écriture z=zcosθ+isinθ avecθ=arg(z)
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr4 Méthode : Ecrire un nombre complexe sous sa forme trigonométrique Vidéo https://youtu.be/zIbpXlgISc4 Ecrire le nombre complexe
z=3+i sous sa forme trigonométrique. - On commence par calculer le module de z : z=3+1=2 - En calculant z z , on peut identifier plus facilement la partie réelle de z et sa partie imaginaire : z z 3 2 1 2 iOn cherche donc un argument θ
de z tel que : cosθ= 3 2 et sinθ= 1 2 . Comme cos 6 3 2 et sin 6 1 2 , on a : z z =cos 6 +isin 6Donc :
z=2cos 6 +isin 6 avec arg(z)= 6 2π. Avec une calculatrice ou un logiciel, il est possible de vérifier les résultats obtenus : 2) Propriétés Inégalité triangulaire : Soit z et z ' deux nombres complexes.
Démonstration : Il s'agit d'une traduction de l'inégalité sur les distances.YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr5 Propriétés : Soit z et z ' deux nombres complexes non nuls et n entier naturel non nul. Produit
zz'=zz' arg(zz')=arg(z)+arg(z')Puissance
z n =z n arg(z n )=narg(z)Inverse
1 z 1 z arg 1 z =-arg(z)Quotient
z z' z z' arg z z' =arg(z)-arg(z')Démonstration pour le produit : On pose
θ=arg(z)
etθ'=arg(z')
zz'=zcosθ+isinθ z'cosθ'+isinθ' =zz'cosθcosθ'-sinθsinθ' +isinθcosθ'+cosθsinθ' =zz'cosθ+θ' +isinθ+θ'Donc le module de
zz' est zz' et un argument de zz' estθ+θ'=arg(z)+arg(z')
. Horsducadredelaclasse,aucunereproduction,mêmepartielle,autresquecellesprévuesàl'articleL122-5ducodedelapropriétéintellectuelle,nepeutêtrefaitedecesitesansl'autorisationexpressedel'auteur.www.maths-et-tiques.fr/index.php/mentions-legales
quotesdbs_dbs33.pdfusesText_39[PDF] équation du second degré ? coefficients complexes
[PDF] controle emc 4eme justice
[PDF] dans classe de mot
[PDF] pour classe de mot
[PDF] tout classe de mot
[PDF] classe de mots tableau
[PDF] très classe de mot
[PDF] classe de mots dictionnaire
[PDF] liste d'adverbe de temps
[PDF] liste des adverbes cm2
[PDF] liste des adverbes en ment
[PDF] liste adverbe de liaison
[PDF] vocabulaire accueillir un client en anglais
[PDF] accueil et secrétariat en anglais pdf
