 Untitled
Untitled
du cours de recherche opérationnelle du CNAM et des centres régionaux comme aux in- qui ont corrigé les épreuves du cours
 Exercice corrigé recherche opérationnelle
Exercice corrigé recherche opérationnelle
L'entreprise AMLAS produit des chaises et des petites tables à partir d'un stock de 16 unités de bois. 10 unités de tissu et emploie un ouvrier qui fournit
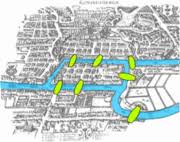 Introduction `a la recherche opérationnelle
Introduction `a la recherche opérationnelle
Un étudiant maıtrisant les exercices de ce cours est capable de proposer une modélisation de nombreux probl`emes de recherche opérationnelle rencontrés dans l'
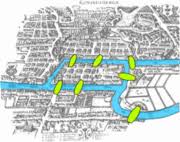 INTRODUCTION À LA RECHERCHE OPÉRATIONNELLE
INTRODUCTION À LA RECHERCHE OPÉRATIONNELLE
Un étudiant maîtrisant les exercices de ce cours est capable de proposer une modélisation d'une grande part des problèmes de recherche opérationnelle rencontrés
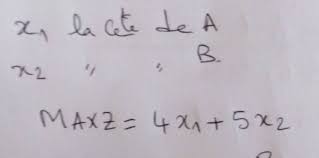 FSJES-AC RECHERCHE OPERATIONNELLE Semestre 6 Filière
FSJES-AC RECHERCHE OPERATIONNELLE Semestre 6 Filière
Tant que la qté de bois reste entre 40 et 60 unités les valeurs marginales des ressources restent valables. EXERCICES AVEC SOLUTIONS. EXERCICE : N°1 -
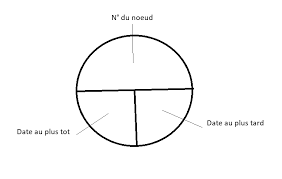 ORDONNANCEMENT Exercices avec solutions
ORDONNANCEMENT Exercices avec solutions
13 avr. 2020 RECHERCHE OPERATIONNELLE. Semestre 6. Filière : Gestion E1-E2-E3. Filière : Economie et Gestion E1 -E2. ✓ ORDONNANCEMENT. « RESEAU PERT – temps ...
 Recherche Opérationnelle:
Recherche Opérationnelle:
Cours de Tronc Commun Scientifique. FICM 2A. Notes de cours et exercices corrigés. Frédéric SUR sur@loria.fr http://www.loria.fr/∼sur/enseignement/RO/. École
 RECHERCHE OPERATIONNELLE
RECHERCHE OPERATIONNELLE
RECHERCHE OPERATIONNELLE – L3 GESTION – M. MEGHRAOUI – SEMESTRE 2. 26. Application numéro 8 : EXERCICES AUTO CORRIGES. Page 21. RECHERCHE OPERATIONNELLE – L3
 Recherche opérationnelle
Recherche opérationnelle
On admettra que ces résultats se généralisent `a un programme linéaire `a n variables. 1.3.6 Exercices. §. ¦. ¤. ¥. Exercice 1.
 Examens avec Solutions Recherche opérationnelle
Examens avec Solutions Recherche opérationnelle
4 – Déterminer le chemin critique. PDF Creator Trial. Page 3. Corrigé de l'examen de la
 Recherche opérationnelle
Recherche opérationnelle
On admettra que ces résultats se généralisent `a un programme linéaire `a n variables. 1.3.6 Exercices. §. ¦. ¤. ¥. Exercice 1.
 Exercice corrigé recherche opérationnelle pdf
Exercice corrigé recherche opérationnelle pdf
planobjet1 Cours. Le RO: Excel Problèmes méthodes
 Recherche Opérationnelle:
Recherche Opérationnelle:
Programmation dynamique chaînes de Markov
 Cahier dexercices corrigés Eric LALLET Jean-Luc RAFFY
Cahier dexercices corrigés Eric LALLET Jean-Luc RAFFY
D'ailleurs pour toutes ces recherches et tout l'aspect logistique
 Examen de recherche opérationnelle – Corrigé
Examen de recherche opérationnelle – Corrigé
Examen de recherche opérationnelle – Corrigé. Marc Roelens. Décembre 2006. 1 Ordonnancement de tâches. 1.1. On dresse le tableau des contraintes de
 Précis de recherche opérationnelle
Précis de recherche opérationnelle
opérationnelle. Méthodes et exercices d'application. Robert Faure était professeur de la chaire de recherche opérationnelle au CNAM. Bernard Lemaire.
 Exercice corrigé de recherche opérationnelle pdf
Exercice corrigé de recherche opérationnelle pdf
Exercice corrigé de recherche opérationnelle pdf. Plan de coursObjet1. La RO : problèmes méthodes
 COURS DE RECHERCHE OPERATIONNELLE
COURS DE RECHERCHE OPERATIONNELLE
Ufr des Sciences Economues et de Gestion. COURS DE RECHERCHE OPERATIONNELLE. ECUE 1 : PROGRAMMATION LINEAIRE. NOTES DE COURS. PAR. Dr Yao Silvère KONAN.
 ORDONNANCEMENT Exercices avec solutions
ORDONNANCEMENT Exercices avec solutions
2020?4?13? RECHERCHE OPERATIONNELLE. Semestre 6. Filière : Gestion E1-E2-E3. Filière : Economie et Gestion E1 -E2. ? ORDONNANCEMENT.
 Examens avec Solutions Recherche opérationnelle
Examens avec Solutions Recherche opérationnelle
Corrigé de l'examen de la session normale. Recherche opérationnelle. Semestre 6 Filière Economie et Gestion Ensembles : 2 et 3 M .ATMANI. Exercice 1.
Présentation Du Cours Recherche Opérationnelle
Définition
Exercices & Examens de Recherche Opérationnelle
Pour télécharger les QCM, exercices et examens de Recherche Opérationnelle, Cliquez sur les liens ci-dessous. 1. Exercices et Examens Corrigés de Recherche Opérationnelle
Recherche Opérationnelle:
Programmation dynamique, chaînes de Markov, files d"attenteCours de Tronc Commun Scientifique
FICM 2A
Notes de cours et exercices corrigés
Frédéric SUR
sur@loria.fr http://www.loria.fr/sur/enseignement/RO/École des Mines de Nancy
2013-2014
(version du 27 février 2014) blablement des coquilles et erreurs. Merci de bien vouloir me les signaler.Il s"agit d"un résumé très condensé de notions dont l"étude approfondie nécessiterait
bien plus de temps. On essaie ici de donner les éléments simplifiés, mais autant que pos- sible rigoureux, de la théorie qui permettent d"aller au delà de l"application de formules. N"hésitez pas à consulter la littérature dédiée.Table des matières
1 La programmation dynamique 7
1.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71.1.1 Un problème de plus court chemin . . . . . . . . . . . . . . . .
71.1.2 Principe d"optimalité de Bellman . . . . . . . . . . . . . . . .
81.2 L"équation de Bellman . . . . . . . . . . . . . . . . . . . . . . . . . .
81.2.1 Un système dynamique . . . . . . . . . . . . . . . . . . . . . .
81.2.2 Équation de Bellman et principe d"optimalité . . . . . . . . . .
91.2.3 Un exemple de recherche de plus courts chemins . . . . . . . .
101.2.4 La résolution d"une équation de Bellman vue comme une re-
cherche de plus courts chemins . . . . . . . . . . . . . . . . . . 101.3 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
131.3.1 La distance d"édition . . . . . . . . . . . . . . . . . . . . . . .
131.3.2 Problème de location de skis . . . . . . . . . . . . . . . . . . .
141.3.3 Équilibrage de charge sur deux machines en parallèle . . . . . .
151.3.4 Un problème d"économie mathématique . . . . . . . . . . . . .
151.3.5 Gestion de stock . . . . . . . . . . . . . . . . . . . . . . . . .
161.3.6 Problème du sac à dos . . . . . . . . . . . . . . . . . . . . . .
172 Les chaînes de Markov 19
2.1 Exemple introductif . . . . . . . . . . . . . . . . . . . . . . . . . . . .
192.2 Vocabulaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
212.2.1 Définitions et premières propriétés . . . . . . . . . . . . . . . .
212.2.2 Représentation graphique des chaînes de Markov . . . . . . . .
222.2.3 Chaînes réductibles et irréductibles . . . . . . . . . . . . . . .
242.2.4 Chaînes périodiques et apériodiques . . . . . . . . . . . . . . .
262.3 Comportement asymptotique des chaînes ergodiques . . . . . . . . . .
272.4 Le " théorème » des coupes . . . . . . . . . . . . . . . . . . . . . . . .
302.5 Comportement asymptotique des chaînes absorbantes . . . . . . . . . .
322.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
352.6.1 L"anatomie d"un moteur de recherche (examen 2010-2011) . . .
352.6.2 Modèle économique de Leontief (examen 2011-2012) . . . . .
363
TABLE DES MATIÈRES 4
2.6.3 Problème de la ruine du joueur (examen 2013-2014) . . . . . .
373 Les files d"attentes 39
3.1 Rappels : loi de Poisson et loi exponentielle . . . . . . . . . . . . . . .
393.2 Caractéristiques d"un système d"attente . . . . . . . . . . . . . . . . .
403.3 La formule de Little . . . . . . . . . . . . . . . . . . . . . . . . . . . .
413.4 Processus de Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . .
443.4.1 Processus de Poisson . . . . . . . . . . . . . . . . . . . . . . .
443.5 Modélisation dans le cadre Markovien . . . . . . . . . . . . . . . . . .
473.5.1 La propriété PASTA . . . . . . . . . . . . . . . . . . . . . . .
473.5.2 Les clients et les serveurs sont sans mémoire . . . . . . . . . .
483.5.3 Les files d"attente M/M/1 . . . . . . . . . . . . . . . . . . . . .
503.5.4 Processus de naissance et de mort . . . . . . . . . . . . . . . .
553.6 Formulaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
573.6.1 File M/M/1 . . . . . . . . . . . . . . . . . . . . . . . . . . . .
583.6.2 File M/M/1/K . . . . . . . . . . . . . . . . . . . . . . . . . . .
583.6.3 File M/M/m . . . . . . . . . . . . . . . . . . . . . . . . . . . .
593.6.4 File M/M/m/m . . . . . . . . . . . . . . . . . . . . . . . . . .
593.7 Les files M/G . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
603.7.1 Processus de Markov par lot . . . . . . . . . . . . . . . . . . .
603.7.2 File M/G/1 générale . . . . . . . . . . . . . . . . . . . . . . .
613.8 Réseaux de files d"attente . . . . . . . . . . . . . . . . . . . . . . . . .
643.9 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
673.9.1 Paradoxe de l"autobus . . . . . . . . . . . . . . . . . . . . . .
673.9.2 Dimensionnement d"un service-client . . . . . . . . . . . . . .
673.9.3 Vélos en libre service (rattrapage 2010-2011) . . . . . . . . . .
673.9.4 Chez le médecin (examen 2010-2011) . . . . . . . . . . . . . .
683.9.5 Un serveur informatique (rattrapage 2011-2012) . . . . . . . .
683.9.6 Problème de maintenance informatique (examen 2010-2011) . .
693.9.7 Étude d"une file M/G/1 (examen 2010-2011) . . . . . . . . . .
693.9.8 Maintenanced"unsystèmeindustrielcritique(examen2011-2012)
703.9.9 Approvisionnement et gestion d"un stock (examen 2013-2014) .
723.9.10 Un guichet avec des clients prioritaires (rattrapage 2013-2014) .
734 Correction des exercices 75
4.1 La programmation dynamique . . . . . . . . . . . . . . . . . . . . . .
764.1.1 La distance d"édition . . . . . . . . . . . . . . . . . . . . . . .
764.1.2 Problème de location de skis . . . . . . . . . . . . . . . . . . .
784.1.3 Équilibrage de charge sur deux machines en parallèle . . . . . .
794.1.4 Un problème d"économie mathématique . . . . . . . . . . . . .
814.1.5 Gestion de stock . . . . . . . . . . . . . . . . . . . . . . . . .
83F. Sur 2013-2014
5 TABLE DES MATIÈRES
4.1.6 Problème du sac à dos . . . . . . . . . . . . . . . . . . . . . .
844.2 Les chaînes de Markov . . . . . . . . . . . . . . . . . . . . . . . . . .
864.2.1 L"anatomie d"un moteur de recherche . . . . . . . . . . . . . .
864.2.2 Modèle économique de Leontief . . . . . . . . . . . . . . . . .
874.2.3 Problème de la ruine du joueur . . . . . . . . . . . . . . . . . .
894.3 Les files d"attente . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
924.3.1 Paradoxe de l"autobus . . . . . . . . . . . . . . . . . . . . . .
924.3.2 Dimensionnement d"un service-client . . . . . . . . . . . . . .
934.3.3 Vélos en libre service . . . . . . . . . . . . . . . . . . . . . . .
944.3.4 Chez le médecin . . . . . . . . . . . . . . . . . . . . . . . . .
954.3.5 Un serveur informatique . . . . . . . . . . . . . . . . . . . . .
964.3.6 Problème de maintenance informatique . . . . . . . . . . . . .
974.3.7 Étude d"une file M/G/1 . . . . . . . . . . . . . . . . . . . . . .
984.3.8 Maintenance d"un système industriel critique . . . . . . . . . .
1004.3.9 Approvisionnement et gestion d"un stock . . . . . . . . . . . .
1034.3.10 Un guichet avec des clients prioritaires . . . . . . . . . . . . .
104Recherche Opérationnelle
TABLE DES MATIÈRES 6
F. Sur 2013-2014
Chapitre 1
La programmation dynamique
1.1 Introduction
1.1.1 Un problème de plus court chemin
On considère le problème du plus court chemin dans un graphe orienté et valué, défini sur un ensemble densommetsf1;2;:::ng. Si les valuations sont positives, l"al- gorithme de Dijkstra permet de trouver le plus court chemin (i.e. le chemin de valuation totale minimale) entre deux sommets. Dans le cas où les valuations peuvent être négatives et où le graphe ne présente pas de circuit de valuation totale négative, nous allons présenter l"algorithme de Floyd-Warshall qui répond à la question.
Notonsd(i;j)la valuation de l"arc(i;j), et (pourk>1)dki;jla longueur du plus court chemin du sommetiau sommetjparmi ceux parcourant uniquement les som- metsf1;2;:::kg. Par convention on suppose aussi : dki;j= +1s"il n"y a pas de chemin deiàj d0i;j=d(i;j)
Le but est de construire un algorithme permettant de calculer lesdni;j.On remarque la propriété suivante.
Proposition 1.1Soitktel que06k6n1. Les(dk+1
i;j)i;jsont liés aux(dki;j)i;jpar la formule de récursion :8(i;j)2 f1;2;:::ng2; dk+1
i;j= mindki;j; dki;k+1+dkk+1;j Démonstration.En effet, si on considère deux sommetsietj: s oitle plus court chemin entre ietjparmi ceux visitantf1;:::;k+ 1gne passe pas par le sommetk+ 1, et alorsdk+1i;j=dki;j;7CHAPITRE 1. LA PROGRAMMATION DYNAMIQUE 8
soit ce plus court chemin passe par le sommet k+ 1. Dans ce cas il ne peut y passer qu"une seule fois (sinon il y a un circuit, de valuation totale positive par hypothèse sur le graphe, que l"on pourrait éliminer pour construire un chemin entreietjplus court, ce qui serait absurde). Ce plus court chemin est donc la concaténation du plus court chemin entreietk+ 1et du plus court chemin entrek+ 1etj, parmi ceux visitant les sommets intermédiairesf1;:::;kguniquement. On a alors :dk+1i;j=dki;k+1+dkk+1;j. L"algorithme de Floyd-Warshall (-Roy) (1962) consiste à calculer les(d1i;j)i;j(en O(n2)opérations, car il y an2paires de sommets(i;j)), puis les(d2i;j)i;j(O(n2) opérations), ..., et finalement les(dni;j)i;j(toujoursO(n2)opérations) qui donnent les longueurs de plus courts chemines cherchées. La complexité totale de l"algorithme est deO(n3).1.1.2 Principe d"optimalité de Bellman
Dans le problème précédent, pour trouver les chemins minimaux sur le graphe, on a résolu des problèmes " plus petits » : trouver les chemins minimaux sur des graphes à k < nsommets. Cette astuce est possible lorsque le problème d"optimisation vérifie le principe d"optimalité de Bellman: une solution optimale pour le problème contient les solutions optimales pour tous les sous-problèmes. Ici, le plus court chemin entre les sommetsietjest la concaténation, pour tout sommet intermédiaireksur ce chemin, du plus court chemin entreietket du plus court chemin entreketj. Laprogrammation dynamiqueconsiste à résoudre les problèmes d"optimisation sat- isfaisant le principe d"optimalité de Bellman en tirant partie d"une formule récursive. L"algorithme de Floyd-Warshall est donc de ce point de vue basé sur la programmation dynamique.1.2 L"équation de Bellman
Il se trouve qu"une classe générale de problèmes d"optimisation satisfait le principe d"optimalité de Bellman. Il s"agit de problèmes dont la fonctionnelle satisfait l"équation de Bellman.1.2.1 Un système dynamique
dont l"état à l"instantt(06t6T) est repéré parxt(valeur scalaire ou vecteur deRd).F. Sur 2013-2014
9 1.2. L"ÉQUATION DE BELLMAN
Soit(xt)l"ensemble des actions possibles lorsque le système est dans l"étatxt. Si l"actionat2(xt)est choisie, le système passe à l"étatxt+1=(xt;at). Notons égalementF(xt;at)le coût de l"actionatlorsque le système est dans l"é- tatxt. Partant de l"état initialx0, le coût global aprèsTpas de temps est alors : T X t=0F(xt;at) Minimiser le profit global revient à résoudre l"équation de Bellman : min a0;:::;aT(
TX t=0F(xt;at);t.q.806t6T; at2(xt)et806t < T; xt+1=(xt;at)) NotonsPT(x)la valeur du coût minimal obtenu en arrivant à l"étatxaprèsTétapes, par-tant de l"étatx0. L"équation précédente donne la valeur dePT(xT+1)(après la dernière
décisionaTle système arrive à l"étatxT+1auquel aucun coût n"est associé). Résoudre l"équation de Bellman consiste à choisir les actionsatguidant le système à chaque pas de temps parmi celles possibles de manière à minimiser le coût global.1.2.2 Équation de Bellman et principe d"optimalité
Ce problème de minimisation peut aussi s"écrire pour tout état finalx: PT(x) = mina2(y)t.q.x=(y;a)fPT1(y) +F(y;a)g
oùPT1(y)désigne le coût minimal réalisable enT1étapes menant à l"étaty. Autrement dit, l"équation de Bellman satisfait le principe d"optimalité de Bellman. La stratégie optimale enTétapes arrivant enxà l"instantTet passant paryà l"in- stantT1contient la stratégie optimale arrivant enyenT1étapes. On peut donc utiliser la programmation dynamique pour résoudre ce problème 1. Pour ce faire, on suppose connaître lesP0(x)pour toutes les valeurs dexpossibles.On calcule alors pour tous lesxpossibles :
P1(x) = mina2(y)t.q.x=(y;a)fP0(y) +F(y;a)g
(cette optimisation n"est pas forcément évidente en pratique, si par exemple(y)n"est qui sont les valeurs qui nous intéressent. La succession des choixa0;a1;:::;aTdonnela stratégie optimale.1. Il semble que certains auteurs réservent l"appellation " programmation dynamique » à la résolution
d"équations de Bellman, régissant justement un systèmedynamique.Recherche Opérationnelle
CHAPITRE 1. LA PROGRAMMATION DYNAMIQUE 10
1.2.3 Un exemple de recherche de plus courts chemins
Considérons le problème des plus courts chemins partant d"un sommets0, dans un grapheGorienté sans circuit mais dont les valuationsd(x;y)peuvent être négatives. SoitdT(s)la longueur du plus court chemin obtenu enTétapes arrivant ens. Alors : dT(sT) = mins
1;:::;sT(
TX t=1d(st1;st)816t6T; st2G(st1)) oùG(s)désigne l"ensemble des successeurs d"un sommetsdu grapheG. On reconnaît l"équation de Bellman. Le " système dynamique » correspondant est le parcours d"un graphe partant du sommets0, et on cherche à minimiser la valuation to- taledT(s). L"actionàprendre quandon estàun étatypermetd"aboutir àunsuccesseurx deyavec un coûtd(x;y). Le problème peut donc se résoudre par la programmation dynamique en résolvant de manière récursive : dT(x) = min
y2G1(x)fd(x;y) +dT1(y)g et on cherchedT(s0); comme le graphe n"a pas de circuit on peut se limiter àT6n. L"algorithme correspondant consiste à appliquer cette formule de récursion avec l"initialisation :d0(s0) = 0etd0(u) = +1siu6=s0. La longueur du plus court chemin partant des0et arrivant à un sommetuest donnée parmin0tndt(u). Cette idée est à la base de l"algorithme de Bellman-Ford permettant de trouver la longueur du plus court chemin entre un sommet donné et tout autre sommet d"un graphe valué.1.2.4 La résolution d"une équation de Bellman vue comme une re-
cherche de plus courts chemins L"exemple précédent montre qu"on peut voir un problème de recherche de plus courts chemins dans un graphe (sans circuit) comme la résolution d"une équation deBellman par programmation dynamique.
est fini, la résolution de l"équation de Bellman décrite dans la section 1.2.1 peut être vue
comme la recherche d"un plus court chemin dans un graphe. Ce graphe est constitué au niveau 0 de l"état de départx0, au niveau1des états possibles pourx1(c"est-à-dire les valeurs décrites par(x0;a)lorsquea2(x0)), au niveau2des états possibles pourx2 (les valeurs décrites par(x1;a)lorsquea2(x1)oùx1est un des états possibles à t= 1), etc., jusqu"au niveauT+1constitué du seul état terminal du systèmexT+1. Il yF. Sur 2013-2014
11 1.2. L"ÉQUATION DE BELLMAN
a un arc entrextetxt1s"il existea2(xt1)tel quext=(xt1;a)(i.e. une action permise dans l"étatxt1menant à l"étatxt), et cet arc est valué parF(xt1;a). La programmation dynamique revient alors à chercher le plus court chemin dex0à x T+1, et la politique optimale est obtenue par propagation arrière (oubacktracking).Un tel graphe est illustré sur la figure 1.1.
Comme on peut le voir sur certains exemples (comme le problème du voyageur de commerce vu en cours), ce graphe peut devenir énorme relativement au niveau maxi- mumT+ 1. Remarquons qu"une équation de Bellman formulée en "max" correspond à la re-cherche d"un plus long chemin dans le graphe associé.t=0 t=1 t=2 t=T=3 t=4FIGURE1.1-Larésolutiondel"équationdeBellmandiscrètevuecommeunerecherche
de plus court chemin, le niveautdu graphe étant constitué des états possibles pour le système à l"instantt. Dans cet exemple, certains étatsxtsont tels que(xt) =;(les sommets correspondants n"ont pas de successeurs), et certains états peuvent être atteints par différentes suites d"actions (les sommets correspondants ont plusieurs antécédents).Recherche Opérationnelle
CHAPITRE 1. LA PROGRAMMATION DYNAMIQUE 12
F. Sur 2013-2014
13 1.3. EXERCICES
1.3 Exercices
1.3.1 La distance d"édition
...aussi appeléedistance de Levenshtein. Soientxetydeux mots sur un alphabet, de longueurs respectivesmetn. On noted(x;y)le nombre minimal d"insertions ou de suppressions de caractères pour passer dexày. L"entierd(x;y)est appelédistance d"éditionentre les motsxety. Par exemple, on peut passer deminesàmimesdes deux manières suivantes : mimes(suppression) La première solution nécessite 2 insertions/suppressions, la seconde 4.Dans cet exemple,d(mines,mimes) = 2.
Questions.
1. Montrez que détablit bien une distance entre mots. 2.Montrez que jmnj6d(x;y)6m+n.
3. Pour i2 f0;1;2;:::;mgetj2 f0;1;2;:::;ng, on notexietyjles préfixes dex etyde longueurs respectivesietj, avec la conventionx0=y0=", où"est le mot vide.Quelles sont les valeurs ded(xi;y0)etd(x0;yj)?
4.Soient i2 f1;:::;mgetj2 f1;:::;ng. Montrez que :
d(xi;yj) = mind(xi1;yj1) + 2i;j; d(xi1;yj) + 1; d(xi;yj1) + 1;(1.1) oùi;jvaut 0 si lai-ème lettre dexet laj-ème lettre deysont identiques, et 1 sinon. 5. Estimez la comple xitéde l"algorithme récursif implémentant " directement » l"équation (1.1). On pourra raisonner sur deux mots de même longueurn. Remarquez que dans cet algorithme les mêmes calculs sont faits plusieurs fois. 6. Déduisez de l"équation (1.1) un algorithme de calcul de d(x;y)tel que le nombre d"opérations et l"occupation mémoire soient enO(mn). 7.Calcul ezd(ingenieur;igneneur).
8. T rouvezune s uited"opérations réalisant le nombre minimal d"opérations dans le cas précédent.Recherche Opérationnelle
CHAPITRE 1. LA PROGRAMMATION DYNAMIQUE 14
Remarque :On définit aussi la distance d"édition comme le nombre minimal d"inser- tions, suppressions ousubstitutions(ces dernières sont bien sûr possibles dans le cadrede l"énoncé, mais " coûtent » ici 2 opérations). On peut aussi donner des coûts différents
à chaque opération. Le principe de la résolution par programmation dynamique reste le même. La distance d"édition est utilisée dans de nombreux contextes (par exemple les cor- recteurs d"orthographe des logiciels de traitement de texte). Une variante est également utilisée dans les problèmes d"alignement de génomesen biologie moléculaire.1.3.2 Problème de location de skis
On cherche à attribuermpaires de skis (de longueursl1;l2;:::;lm) ànskieurs (de taillest1;t2;:::;tn), de manière à minimiser la somme des différences entre la longueur des skis et la taille des skieurs.Bien sûr,n6m.
Le problème consiste à trouver une fonction (d"allocation)atelle que le skieur noi se voit attribuer la paire de skis n oa(i)et qui minimise : n X i=1 tila(i) La même paire de skis n"est pas attribuée à deux skieurs, donc la fonctionaest injective.Questions.
1. Montrez que l"optimum est atteint par une fonction acroissante. On supposera donc que l"affectation des skis desipremiers skieurs se fait parmi lesjpremières paires de skis. 2. Soit Si;jle minimum de la fonction-objectif du problème restreint auxipremiers skieurs etjpremières paires de skis.Montrez que
S(i;j) = minS(i;j1);S(i1;j1) +jtiljj:
3. Comme ntprocéderiez-v ouspour calculer la solution optimale ? 4.Quelle est la comple xitéde cet algorithme ?
F. Sur 2013-2014
15 1.3. EXERCICES
1.3.3 Équilibrage de charge sur deux machines en parallèle
On considère deux machines (par exemple des machines industrielles, mais aussi des processeurs) sur lesquelles sont exécutéesntâches de duréest1;t2;:::tn. On souhaite répartir les tâches sur chacune des machines de manière à ce qu"elles s"arrêtent au plus tôt.Questions.
1. Justifiez que le b utest de partitionner l"ensemble des ntâches en deux sous- ensemblesA1etA2, l"un s"exécutant sur la machine 1, l"autre sur la machine 2, tels quequotesdbs_dbs10.pdfusesText_16[PDF] methode boscher pdf download
[PDF] méthode boscher cahier de lecture pdf
[PDF] methode boscher en ligne
[PDF] méthode boscher gratuit
[PDF] méthode boscher cahier des sons pdf
[PDF] adjectif pour acrostiche
[PDF] recherche qualitative définition
[PDF] méthode qualitative et quantitative
[PDF] méthode qualitative mémoire
[PDF] méthode quantitative
[PDF] méthodologie de recherche qualitative pdf
[PDF] méthode qualitative entretien
[PDF] méthode qualitative sociologie
[PDF] mémoire kiné traumatologie
