[PDF] [PDF] Exo7 - Exercices de mathématiques





Previous PDF Next PDF



Dérivation

Calculons la dérivée n-ième de la fonction réelle t ↦→ cos(t)et cos3 x = 1. 4. (3 cos x + cos 3x). On sait. (cos x)(n) = cos(x + nπ/2) et (cos 3x)(n) = 3n ...





Dérivées des fonctions x ↦− → sin(ax + b) et x ↦− → cos(ax + b).

x étant un réel quelconque et a = 0 étudions les limites des rapports sin(a(x + h) + b) − sin(ax + b) h et cos(a(x + h) + b) − cos(ax + b).



MATHS 110c cHAPITRE V : DÉRIVABILITÉ Après avoir rappelé les

(1) M o n t rer que l 'o n a x cos x - s in x < 0 si x ∈ ] 0 ¢ ] . ( 2 )E Supposons que la dérivée n -ième



Dérivées successives - Formules de Taylor

cos ∈ C. ∞. (R) et sin ∈ C. ∞. (R). 6. tan ∈ C. ∞. (. R . {. (2k + 1) Il n'y a pas de formule pour calculer la dérivée n-ième d'un quotient ou d'une ...



MATHS Rappels Equations Différentielles

y(n) la dérivée nième de y par rapport à x. L'équation différentielle sera y(x) = Ax cos(ax) + Bx sin(ax). • Exemple 3.17: Résoudre (E17) y − 3y + 2y = 3 ...



Université de Cergy-Pontoise Département de Mathématiques

Exercice 1.6 Déterminer les dérivées nieme des fonctions suivantes : 1. f(x) = 1 x. 2. g(x) = 1 x2. 3. h(x) = ax+b cx+d. 4. i(x)=3xk. 5. j(x) = cos(2x). 6. k(x) 



Dérivabilité - Théorèmes de Rolle théorème des accroissements

26 févr. 2015 Montrer que si f s'annule (n + 1) fois alors sa dérivée n-ième s'annule au moins une fois. ... ne change pas lorsqu'on la dérive : la fonction ...



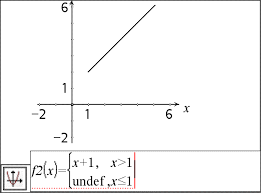TI-Nspire™ CAS / TI-Nspire™ CX CAS Guide de référence TI-Nspire™ CAS / TI-Nspire™ CX CAS Guide de référence

ne contient donc pas cos() si et seulement si cos. (...) dans l'expression ... dérivée ou dérivée n-ième. 10 dérivée première. 9 dérivée seconde. 10 e ...





Dérivées des fonctions x ?? ? sin(ax + b) et x ?? ? cos(ax + b).

Dérivées des fonctions x ?? ? sin(ax + b) et x ?? ? cos(ax + b). ah = 0 et la fonction sinus est dérivable en ax + b donc.



Calculer pour tout entier n

http://www.panamaths.net/Documents/Exercices/SolutionsPDF/16/DERIV00041.pdf



Exo7 - Cours de mathématiques

on note f (n) la dérivée n-ième de f . Pour tout n dans N calculer la dérivée n-ième de : • f : x ? cos(x). • g : x ? eax+b avec a



Fonctions dérivables 1 Calculs

Montrer que le polynôme Xn +aX +b (a et b réels) admet au plus trois racines réelles. On veut montrer que pour t < 0



M.P.S.I. Colles

Sujet 1. EX 1. EX 2. EX 3. M.P.S.I.



Dérivabilité - Théorèmes de Rolle théorème des accroissements

Feb 26 2015 fois alors sa dérivée n-ième s'annule au moins une fois. ... 3 en zéro des fonctions x ?? ln(1 + x)



Développements limités

fonction dérivable n ? 1 fois sur I et dont la dérivée n-ième en 0 existe. Il est à noter que les développements du sinus et cosinus ordinaires ...



MATHS Rappels Equations Différentielles

cas particuliers : f(x) = K sin(ax) ou f(x) = K cos(ax) . . . . . . . . 22. Maths Rappels y(n) la dérivée nième de y par rapport à x.



Dérivation

Calculer la dérivée n-ième de x ?? cos3 x. Exercice 14 [ 03863 ] [Correction]. Calculons la dérivée n-ième de la fonction réelle t ?? cos(t)et.





[PDF] DERIVATION (COURS-EXERCICES) YjY 1 Dérivation premières

On en déduit enfin la dérivée de la fonction cosinus ((cos)? = ?sin ) avec la formule cos(x) = sin(x + ?/2) (exercice) Propriétés : Soient I =]a 



[PDF] Dérivées des fonctions x ?? ? sin(ax + b) et x - lycee-valin

Si a et b sont deux réels quelconques alors : • la fonction x ?? ? sin(ax + b) est dérivable sur R et sa fonction dérivée est la fonction x ?? ? a cos(ax 



Calcul de dérivées n-ième - dDMaths

Calculer la dérivée n-ième de la fonction réelle t?cos(t)et



[PDF] Sommaire (liens internes au document) :

Il s'agit de déterminer l'expres- sion de la dérivée n ième d'une fonction en conjecturant d'abord la formule par "reconnaissance de formes algébriques" sur 



[PDF] MAT111 CHAPITRE 2 : DÉRIVATION 1 Quelques fonctions usuelles

Fonctions affines : f(x) = ax + b où a et b sont des réels générale si f est dérivable n fois sur I la dérivée n-ième de f notée f(n) est donnée



[PDF] Dérivée dune fonction - Exo7 - Cours de mathématiques

Ainsi on a obtenu une n-ième racine réelle ?n (pas nécessairement distincte des autres ?i) Mini-exercices 1 Dessiner le graphe de fonctions vérifiant : f1 



[PDF] Dérivation - Xiffr

Calculons la dérivée n-ième de la fonction réelle t ?? cos(t)et En dérivant la relation par rapport à x on obtient : f (x + y) = f (x)



[PDF] MATHS 110c cHAPITRE V : DÉRIVABILITÉ Après avoir rappelé les

la dérivée de x y par rapport à x est y Exemple 2 : Soit /(x y ) = cos (x y ) C ette fonction est définie pour tout (x y ) dans R 2 Alors

  • Comment dériver cos et sin ?

    La dérivée de cosinus est égale à un sinus négatif, et la dérivée de sinus est égale à un cosinus positif. Astuce pour la Dérivée : Pour l'astuce, on se concentre uniquement sur la dérivée de cosinus, car la dérivée de sinus est simple, il suffit de transformer le sinus en cosinus.

  • Comment calculer la dérivée nième ?

    dndxn(cos(x))=cos(x+n?2) et dndxn(sin(x))=sin(x+n?2). (x2(1+x)n)(n)=n

  • Quelle est la dérivée de ax ?

    Règle : La règle de dérivation en chaîne
    Pour deux fonctions dérivables �� ( �� ) et �� ( �� ) , la dérivée de leur fonction composée �� ( �� ( �� ) ) est : d d d d d d �� ( �� ( �� ( �� ) ) ) = �� �� �� �� . On peut écrire cette règle de manière plus succincte en utilisant la notation prime : ( �� ( �� ) ) ? = �� ? ( �� ) �� ? .
[PDF] Exo7 - Exercices de mathématiques Exo7

Fonctions dérivables

1 Calculs

Exercice 1Déterminera;b2Rde manière à ce que la fonctionfdéfinie surR+par : f(x) =pxsi 06x61 etf(x) =ax2+bx+1 six>1 soit dérivable surR+.

Soitf:R!Rdéfinie parf(x) =x2sin1x

. Montrer quefest prolongeable par continuité en 0 ; on note encorefla fonction prolongée. Montrer quefest dérivable surRmais quef0n"est pas continue en 0. Étudier la dérivabilité des fonctions suivantes : f

1(x) =x2cos1x

;six6=0 ;f1(0) =0; f

2(x) =sinxsin1x

;six6=0 ;f2(0) =0; f

3(x) =jxjpx

22x+1x1;six6=1 ;f3(1) =1:

Soitn>2 un entier fixé etf:R+= [0;+¥[!Rla fonction définie par la formule suivante: f(x) =1+xn(1+x)n;x>0: 1. (a) Montrer que fest dérivable surR+et calculerf0(x)pourx>0: (b) En étudiantlesignedef0(x)surR+;montrerquefatteintunminimumsurR+quel"ondéterminera. 2. (a)

En déduire l"inég alitésui vante:

(1+x)n62n1(1+xn);8x2R+: (b)

Montrer que si x2R+ety2R+alors on a

(x+y)n62n1(xn+yn):

2 Théorème de Rolle et accroissements finis

Exercice 5Montrer que le polynômeXn+aX+b, (aetbréels) admet au plus trois racines réelles.

Montrer que le polynômePndéfini par

P n(t) =h1t2ni(n)

est un polynôme de degréndont les racines sont réelles, simples, et appartiennent à[1;1].

Dans l"application du théorème des accroissements finis à la fonction f(x) =ax2+bx+g

sur l"intervalle[a;b]préciser le nombre "c" de]a;b[. Donner une interprétation géométrique.

Soientxetyréels avec 0 1.

Montrer que

xDe l"étude defdéduire que pour toutade]0;1[

alnx+(1a)lnyInterprétation géométrique ? Exercice 9Déterminer les extremums def(x) =x4x3+1 surR. Soientf;g:[a;b]!Rdeux fonctions continues sur[a;b](a0(x)6=0 pour toutx2]a;b[: 1.

Montrer que g(x)6=g(a)pour toutx2]a;b[:

2

2.Posons p=f(b)f(a)g(b)g(a)et considérons la fonctionh(x)=f(x)pg(x)pourx2[a;b]:Montrer quehvérifie

les hypothèses du théorème de Rolle et en déduire qu"il existe un nombre réelc2]a;b[tel que

f(a)f(b)g(a)g(b)=f0(c)g 0(c): 3.

On suppose que lim

x!bf0(x)g

0(x)=`;où`est un nombre réel. Montrer que

lim x!bf(x)f(b)g(x)g(b)=`:

4.Application.Calculer la limite suivante:

lim x!1arccosxp1x2:

On considère la fonctionf:R!Rdéfinie par

f(t) =( e1=tsit<0

0 sit>0

1. Démontrer que fest dérivable surR, en particulier ent=0. 2.

Etudier l"e xistencede f00(0).

3. On v eutmontrer que pour t<0, la dérivéen-ième defs"écrit f (n)(t) =Pn(t)t

2ne1=t

oùPnest un polynôme. (a)

T rouverP1etP2.

(b) T rouverune relation de récurrence entre Pn+1;PnetP0npourn2N. 4.

Montrer que fest de classeC¥.

Indication pourl"exer cice1 NVous avez deux conditions : il faut que la fonction soit continue (car on veut qu"elle soit dérivable donc elle

doit être continue) et ensuite la condition de dérivabilité proprement dite.Indication pourl"exer cice2 Nfest continue en 0 en la prolongeant parf(0) =0.fest alors dérivable en 0 etf0(0) =0.Indication pourl"exer cice3 NLes problèmes sont seulement en 0 ou 1.f1est dérivable en 0 mais pasf2.f3n"est dérivable ni en 0, ni en 1.Indication pourl"exer cice5 NOn peut appliquer le théorème de Rolle plusieurs fois.

Indication pour

l"exer cice

6 NIl faut appliquer le théorème de Rolle une fois au polynôme(1t2)n, puis deux fois à sa dérivée première, puis

trois fois à sa dérivée seconde,...Indication pourl"exer cice8 N1.Utiliser le théorème des accroissements finis a vecla fonction t7!lnt

2.

Montrer d"abord que f00est négative. Se servir du théorème des valeurs intermédiaires pourf0.Indication pourl"exer cice10 N1.Raisonner par l"absurde et appliquer le théorème de Rolle.

2.

Calculer h(a)eth(b).

3.

Appliquer la question 2. sur l"interv alle[x;b].

4.

Calculer f0etg0.4

Correction del"exer cice1 NLa fonctionfest continue et dérivable sur]0;1[et sur]1;+¥[. Le seul problème est enx=1.

Il faut d"abord que la fonction soit continue enx=1. La limite à gauche est limx!1px= +1 et à droite

lim x!1+ax2+bx+1=a+b+1. Donca+b+1=1. Autrement ditb=a.

Il faut maintenant que les dérivées à droite et à gauche soient égales. Comme la fonctionfrestreinte à]0;1]

est définie parx7!pxalors elle est dérivable à gauche et la dérivée à gauche s"obtient en évaluant la fonction

dérivéex7!12 px enx=1. Doncf0g(1) =12 Pour la dérivée à droite il s"agit de calculer la limite du taux d"accroissement f(x)f(1)x1, lorsquex!1 avec x>1. Orf(x)f(1)x1=ax2+bx+11x1=ax2axx1=ax(x1)x1=ax:

Doncfest dérivable à droite etf0d(1) =a. Afin quefsoit dérivable, il faut et il suffit que les dérivées à droite

et à gauche existent et soient égales, donc ici la condition esta=12 Le seul couple(a;b)que rendfdérivable sur]0;+¥[est(a=12 ;b=12 ).Correction del"exer cice2 NfestC¥surR. 1. Comme jsin(1=x)j61 alorsftend vers 0 quandx!0. Donc en prolongeantfparf(0) =0, la fonction fprolongée est continue surR. 2.

Le taux d"accroissement est

f(x)f(0)x0=xsin1x Comme ci-dessus il y a une limite (qui vaut 0) enx=0. Doncfest dérivable en 0 etf0(0) =0. 3. Sur R,f0(x) =2xsin(1=x)cos(1=x), Doncf0(x)n"a pas de limite quandx!0. Doncf0n"est pas

continue en 0.Correction del"exer cice3 N1.La fonction f1est dérivable en dehors dex=0. En effetx7!1x

est dérivable surRetx7!cosxest dérivable surR, donc par compositionx7!cos1x est dérivable surR. Puis par multiplication par la

fonction dérivablex7!x2, la fonctionf1est dérivable surR. Par la suite on omet souvent ce genre de

discussion ou on l"abrège sous la forme "fest dérivable surIcomme somme, produit, composition de

fonctions dérivables surI". Pour savoir sif1est dérivable en 0 regardons le taux d"accroissement: f

1(x)f1(0)x0=xcos1x

Maisxcos(1=x)tend vers 0 (six!0) carjcos(1=x)j61. Donc le taux d"accroissement tend vers 0.

Doncf1est dérivable en 0 etf01(0) =0.

2. Encore une fois f2est dérivable en dehors de 0. Le taux d"accroissement enx=0 est : f

2(x)f2(0)x0=sinxx

sin1x

Nous savons que

sinxx !1 et que sin1=xn"a pas de limite quandx!0. Donc le taux d"accroissement n"a pas de limite, doncf2n"est pas dérivable en 0. 3.

La fonction f3s"écrit :

f

3(x) =jxjjx1jx1:

5 •Donc pour x>1 on af3(x) =x; pour 06x<1 on af3(x) =x; pourx<0 on af3(x) =x.

La fonction f3est définie, continue et dérivable surRnf0;1g. Attention ! La fonctionx7! jxjn"est

pas dérivable en 0. La fonction f3n"est pas continue en 1, en effet limx!1+f3(x) = +1 et limx!1f3(x) =1. Donc la fonction n"est pas dérivable en 1. La fonction f3est continue en 0. Le taux d"accroissement pourx>0 est f

3(x)f3(0)x0=xx

=1 et pourx<0, f

3(x)f3(0)x0=xx

= +1:

Donc le taux d"accroissement n"a pas de limite en 0 et doncf3n"est pas dérivable en 0.Correction del"exer cice4 N1.(a) Il est clair que la fonction fest dérivable surR+puisque c"est une fonction rationnelle sans pôle

dans cet intervalle. De plus d"après la formule de la dérivée d"un quotient, on obtient pourx>0 :

f

0(x) =n(xn11)(1+x)n+1:

(b) P arl"e xpressionprécédente f0(x)est du signe dexn11 surR+:Par conséquent on obtient: f

0(x)60 pour 06x61 etf0(x)>0 pourx>1:Il en résulte quefest décroissante sur[0;1]et

croissante sur[1;+¥[et par suitefatteint son minimum surR+au point 1 et ce minimum vaut f(1) =21n: 2. (a) Il résulte de la question 1.b que f(x)>f(1)pour toutx2R+et donc (1+x)n62n1(1+xn): (b)

En appliquant l"inég alitéprécédente a vecx=b=a;on en déduit immédiatement l"inégalité requise

(le cas du couple(0;0)étant trivial).Correction del"exer cice5 N1.P arl"absurde on suppose qu"il y a (au moins) quatre racines distinctes pour Pn(X)=Xn+aX+b. Notons

lesx1

existex01 x

02etx03. On obtient deux racines distinctes pourP00n. OrP00n=n(n1)Xn2ne peut avoir que 0 comme

racines. Donc nous avons obtenu une contradiction.

2.Autre méthode :Le résultat est évident sin63:On suppose doncn>3:SoitPnl"applicationX7!

X n+aX+bdeRdans lui-même. AlorsP0n(X) =nXn1+as"annule en au plus deux valeurs. DoncPn

est successivement croissante-décroissante-croissante ou bien décroissante-croissante-décroissante. Et

doncPns"annule au plus trois fois.Correction del"exer cice6 NQ

n(t) = (1t2)nest un polynôme de degré 2n, on le dérivenfois, on obtient un polynôme de degrén. Les

valeurs1 et+1 sont des racines d"ordrendeQn, doncQn(1) =Q0n(1) =:::=Q(n1)n(1) =0. Même chose

en1. EnfinQ(1) =0=Q(+1)donc d"après le théorème de Rolle il existec2]1;1[telle queQ0n(c) =0.

6

DoncQ0n(1) =0,Q0n(c) =0,Q0n(1) =0. En appliquant le théorème de Rolle deux fois (sur[1;c]et sur

[c;+1]), on obtient l"existence de racinesd1;d2pourQ00n, qui s"ajoutent aux racines1 et+1.

On continue ainsi par récurrence. On obtient pourQ(n1)n,n+1 racines:1;e1;:::;en1;+1. Nous appliquons

le théorème de Rollenfois. Nous obtenonsnracines pourPn=Q(n)n. Comme un polynôme de degréna au

plusnracines, nous avons obtenu toutes les racines. Par constructions ces racines sont réelles distinctes, donc

simples.Correction del"exer cice7 NLa fonctionfest continue et dérivable surRdonc en particulier sur[a;b]. Le théorème des accroissement finis

assure l"existence d"un nombrec2]a;b[tel quef(b)f(a) =f0(c)(ba).

Mais pour la fonction particulière de cet exercice nous pouvons expliciter cec. En effetf(b)f(a)=f0(c)(b

a)impliquea(b2a2)+b(ba) = (2ac+b)(ba). Doncc=a+b2 Géométriquement, le graphePdefest une parabole. Si l"on prend deux pointsA= (a;f(a))etB=

(b;f(b))appartenant à cette parabole, alors la droite(AB)est parallèle à la tangente enPqui passe en

M= (a+b2

;f(a+b2

)). L"abscisse deMétant le milieu des abscisses deAetB.Correction del"exer cice8 N1.Soit g(t)=lnt. Appliquonslethéorèmedesaccroissementsfinissur[x;y]. Ilexistec2]x;y[,g(y)g(x)=

g

0(c)(yx). Soit lnylnx=1c

(yx). Donclnylnxyx=1c . Orx2.f0(a)=xyax+(1a)ylnx+lny. Etf00(a)=(xy)2(ax+(1a)y)2. Commef00estnégativealorsf0estdécroissante sur[0;1]. Orf0(0) =xyy(lnxlny)y >0 d"après la première question et de mêmef0(1)<0. Par le

théorème des valeurs intermédiaires, il existec2[x;y]tel quef0(c) =0. Maintenantf0est positive sur

[0;c]et négative sur[c;1]. Doncfest croissante sur[0;c]et décroissante sur[c;1]. Orf(0) =0 et f(1) =0 donc pour toutx2[0;1],f(x)>0. Cela prouve l"inégalité demandée. 3.

Géométriquement nous a vonsprouvé que la fonction ln est conca ve,c"est-à-dire que la corde (le se gment

qui va de(x;f(x))à(y;f(y)) est sous la courbe d"équationy=f(x).Correction del"exer cice9 Nf

0(x) =4x33x2=x2(4x3)donc les extremums appartiennent àf0;34

g. Commef00(x) =12x26x=

6x(2x1). Alorsf00ne s"annule pas en34

, donc34 donne un extremum local (qui est même un minimum

global). Par contref00(0) =0 etf000(0)6=0 donc 0 est un point d"inflexion qui n"est pas un extremum (même

pas local, pensez à un fonction du typex7!x3).Correction del"exer cice10 NLe théorème de Rolle dit que sih:[a;b]!Rest une fonction continue sur l"intervalle fermé[a;b]et dérivable

sur l"ouvert]a;b[alors il existec2]a;b[tel queh0(c) =0: 1.

Supposons par l"absurde, qu"il e xistex02]a;b]tel queg(x0) =g(a):Alors en appliquant le théorème de

Rolle à la restriction degà l"intervalle[a;x0](les hypothèses étant clairement vérifiées), on en déduit

qu"il existec2]a;x0[tel queg0(c) =0;ce qui contredit les hypothèses faites surg:Par conséquent on a

démontré queg(x)6=g(a)pour toutx2]a;b]: 2.

D"après la question précédente, on a en particulier g(b)6=g(a)et doncpest un nombre réel bien défini

eth=fpgest alors une fonction continue sur[a;b]et dérivable sur]a;b[:Un calcul simple montre

queh(a) =h(b):D"après le théorème de Rolle il en résulte qu"il existec2]a;b[tel queh0(c) =0:Ce qui

implique la relation requise. 7

3.Pour chaque x2]a;b[;on peut appliquer la question 2. aux restrictions defetgà l"intervalle[x;b];on en

déduit qu"il existe un pointc(x)2]x;b[;dépendant dextel que ()f(x)f(b)g(x)g(b)=f0(c(x))g

0(c(x)):

Alors, comme lim

x!bf0(t)g

0(t)=`et limx!bc(x) =b;(carc(x)2]x;b[) on en déduit en passant à la limite

dans()que lim x!bf(x)f(b)g(x)g(b)=`: Ce résultat est connu sous le nom de "règle de l"Hôpital". 4. Considérons les deux fonctions f(x) =arccosxetg(x) =p1x2pourx2[0;1]:Ces fonctions sont continues sur[0;1]et dérivables sur]0;1[etf0(x) =1=p1x2,g0(x) =x=p1x26=0 pour tout x2]0;1[:En appliquant les résultats de la question 3., on en déduit que lim x!1arccosxp1x2=limx!11p1x2xp1x2=limx!11x

=1:Correction del"exer cice11 N1.fest dérivable surRen tant que composée de fonctions dérivables, et surR+car elle est nulle sur cet

intervalle ; étudions donc la dérivabilité en 0. On a f(t)f(0)t e1=t=tsit<0

0 sit>0

ore1=t=ttend vers 0 quandttend vers 0 par valeurs négatives. Doncfest dérivable à gauche et à droite

en 0 et ces dérivées sont identiques, doncfest dérivable etf0(0) =0. 2. On a f

0(t) =(

e1=t=t2sit<0

0 sit>0

donc le taux d"accroissement def0au voisinage de 0 est f

0(t)f0(0)t

e1=t=t3sit<0

0 sit>0

et il tend vers 0 quandttend vers 0 par valeurs supérieures comme inférieures. Doncfadmet une dérivée

seconde en 0, etf00(0) =0. 3. (a) On a déjà trouvé que f0(t) =e1=t=t2, doncf0(t) =P1(t)=t2e1=tsi on poseP1(t) =1.

Par ailleurs,f00(t) =e1=t=t4+e1=t(2=t3) =1+2tt

4e1=tdonc la formule est vraie pourn=2 en posant

P

2(t) =1+2t.

(b) Supposons que la formule est vraie au rang n. Alorsf(n)(t) =Pn(t)t

2ne1=td"où

f (n+1)(t) =P0n(t)t2nPn(t)(2n)t2n1t

4ne1=t+Pn(t)t

2ne1=t(1=t2)

P0n(t)t2(2nt+1)Pn(t)t

2(n+1)e1=t

donc la formule est vraie au rangn+1 avec P n+1(t) =P0n(t)t2(2nt+1)Pn(t): 8

4.Sur Ret surR+,fest indéfiniment dérivable, donc il suffit d"étudier ce qui se passe en 0.

Montrons par récurrence quefest indéfiniment dérivable en 0, et que pour toutn2N;f(n)(0) =0. On

sait que c"est vrai au rang 1. Supposons quefestn-fois dérivable, et quef(n)(0) =0. Alors le taux d"accroissement def(n)en 0 est : f (n)(t)f(n)(0)t P n(t)e1=t=t2n+1sit<0

0 sit>0

et sa limite est 0 quandttend vers 0 par valeurs supérieures comme inférieures. Doncf(n)est dérivable

en 0, etf(n+1)(0) =0. Donc l"hypothèse de récurrence est vérifiée au rangn+1.

Par conséquent,fest de classeC¥.9

quotesdbs_dbs33.pdfusesText_39
[PDF] dérivées partielles exercices corrigés

[PDF] dérivée partielle pdf

[PDF] différentielle totale

[PDF] dérivée partielle fonction composée

[PDF] dérivées partielles secondes

[PDF] dérivée totale

[PDF] différentielle totale exemple

[PDF] dérivée racine carrée

[PDF] dérivée u puissance n

[PDF] formule dérivée

[PDF] dérivée seconde exponentielle

[PDF] convexe

[PDF] nombre dérivé 1ere sti2d

[PDF] primitive terminale sti2d

[PDF] tableau dérivée sti2d