[PDF] MATHS Rappels Equations Différentielles





Previous PDF Next PDF



Dérivation

Calculons la dérivée n-ième de la fonction réelle t ↦→ cos(t)et cos3 x = 1. 4. (3 cos x + cos 3x). On sait. (cos x)(n) = cos(x + nπ/2) et (cos 3x)(n) = 3n ...





Dérivées des fonctions x ↦− → sin(ax + b) et x ↦− → cos(ax + b).

x étant un réel quelconque et a = 0 étudions les limites des rapports sin(a(x + h) + b) − sin(ax + b) h et cos(a(x + h) + b) − cos(ax + b).



MATHS 110c cHAPITRE V : DÉRIVABILITÉ Après avoir rappelé les

(1) M o n t rer que l 'o n a x cos x - s in x < 0 si x ∈ ] 0 ¢ ] . ( 2 )E Supposons que la dérivée n -ième



Dérivées successives - Formules de Taylor

cos ∈ C. ∞. (R) et sin ∈ C. ∞. (R). 6. tan ∈ C. ∞. (. R . {. (2k + 1) Il n'y a pas de formule pour calculer la dérivée n-ième d'un quotient ou d'une ...



[PDF] Exo7 - Exercices de mathématiques

On veut montrer que pour t < 0 la dérivée n-ième de f s'écrit f. (n)(t) = Pn Mais xcos(1/x) tend vers 0 (si x → 0) car



Université de Cergy-Pontoise Département de Mathématiques

Exercice 1.6 Déterminer les dérivées nieme des fonctions suivantes : 1. f(x) = 1 x. 2. g(x) = 1 x2. 3. h(x) = ax+b cx+d. 4. i(x)=3xk. 5. j(x) = cos(2x). 6. k(x) 



Dérivabilité - Théorèmes de Rolle théorème des accroissements

26 févr. 2015 Montrer que si f s'annule (n + 1) fois alors sa dérivée n-ième s'annule au moins une fois. ... ne change pas lorsqu'on la dérive : la fonction ...



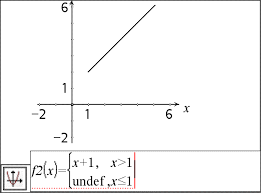TI-Nspire™ CAS / TI-Nspire™ CX CAS Guide de référence TI-Nspire™ CAS / TI-Nspire™ CX CAS Guide de référence

ne contient donc pas cos() si et seulement si cos. (...) dans l'expression ... dérivée ou dérivée n-ième. 10 dérivée première. 9 dérivée seconde. 10 e ...





Dérivées des fonctions x ?? ? sin(ax + b) et x ?? ? cos(ax + b).

Dérivées des fonctions x ?? ? sin(ax + b) et x ?? ? cos(ax + b). ah = 0 et la fonction sinus est dérivable en ax + b donc.



Calculer pour tout entier n

http://www.panamaths.net/Documents/Exercices/SolutionsPDF/16/DERIV00041.pdf



Exo7 - Cours de mathématiques

on note f (n) la dérivée n-ième de f . Pour tout n dans N calculer la dérivée n-ième de : • f : x ? cos(x). • g : x ? eax+b avec a



Fonctions dérivables 1 Calculs

Montrer que le polynôme Xn +aX +b (a et b réels) admet au plus trois racines réelles. On veut montrer que pour t < 0



M.P.S.I. Colles

Sujet 1. EX 1. EX 2. EX 3. M.P.S.I.



Dérivabilité - Théorèmes de Rolle théorème des accroissements

Feb 26 2015 fois alors sa dérivée n-ième s'annule au moins une fois. ... 3 en zéro des fonctions x ?? ln(1 + x)



Développements limités

fonction dérivable n ? 1 fois sur I et dont la dérivée n-ième en 0 existe. Il est à noter que les développements du sinus et cosinus ordinaires ...



MATHS Rappels Equations Différentielles

cas particuliers : f(x) = K sin(ax) ou f(x) = K cos(ax) . . . . . . . . 22. Maths Rappels y(n) la dérivée nième de y par rapport à x.



Dérivation

Calculer la dérivée n-ième de x ?? cos3 x. Exercice 14 [ 03863 ] [Correction]. Calculons la dérivée n-ième de la fonction réelle t ?? cos(t)et.





[PDF] DERIVATION (COURS-EXERCICES) YjY 1 Dérivation premières

On en déduit enfin la dérivée de la fonction cosinus ((cos)? = ?sin ) avec la formule cos(x) = sin(x + ?/2) (exercice) Propriétés : Soient I =]a 



[PDF] Dérivées des fonctions x ?? ? sin(ax + b) et x - lycee-valin

Si a et b sont deux réels quelconques alors : • la fonction x ?? ? sin(ax + b) est dérivable sur R et sa fonction dérivée est la fonction x ?? ? a cos(ax 



Calcul de dérivées n-ième - dDMaths

Calculer la dérivée n-ième de la fonction réelle t?cos(t)et



[PDF] Sommaire (liens internes au document) :

Il s'agit de déterminer l'expres- sion de la dérivée n ième d'une fonction en conjecturant d'abord la formule par "reconnaissance de formes algébriques" sur 



[PDF] MAT111 CHAPITRE 2 : DÉRIVATION 1 Quelques fonctions usuelles

Fonctions affines : f(x) = ax + b où a et b sont des réels générale si f est dérivable n fois sur I la dérivée n-ième de f notée f(n) est donnée



[PDF] Dérivée dune fonction - Exo7 - Cours de mathématiques

Ainsi on a obtenu une n-ième racine réelle ?n (pas nécessairement distincte des autres ?i) Mini-exercices 1 Dessiner le graphe de fonctions vérifiant : f1 



[PDF] Dérivation - Xiffr

Calculons la dérivée n-ième de la fonction réelle t ?? cos(t)et En dérivant la relation par rapport à x on obtient : f (x + y) = f (x)



[PDF] MATHS 110c cHAPITRE V : DÉRIVABILITÉ Après avoir rappelé les

la dérivée de x y par rapport à x est y Exemple 2 : Soit /(x y ) = cos (x y ) C ette fonction est définie pour tout (x y ) dans R 2 Alors

  • Comment dériver cos et sin ?

    La dérivée de cosinus est égale à un sinus négatif, et la dérivée de sinus est égale à un cosinus positif. Astuce pour la Dérivée : Pour l'astuce, on se concentre uniquement sur la dérivée de cosinus, car la dérivée de sinus est simple, il suffit de transformer le sinus en cosinus.

  • Comment calculer la dérivée nième ?

    dndxn(cos(x))=cos(x+n?2) et dndxn(sin(x))=sin(x+n?2). (x2(1+x)n)(n)=n

  • Quelle est la dérivée de ax ?

    Règle : La règle de dérivation en chaîne
    Pour deux fonctions dérivables �� ( �� ) et �� ( �� ) , la dérivée de leur fonction composée �� ( �� ( �� ) ) est : d d d d d d �� ( �� ( �� ( �� ) ) ) = �� �� �� �� . On peut écrire cette règle de manière plus succincte en utilisant la notation prime : ( �� ( �� ) ) ? = �� ? ( �� ) �� ? .
MATHS Rappels Equations Différentielles

INSTITUT NATIONAL POLYTECHNIQUE DE TOULOUSE

MATHS Rappels

Equations Différentielles

Jean-Pierre Bourgade

Pascal Floquet Première Année à Distance Septembre 2011

Xuân Meyer

2

Maths Rappels

Table des matières3 Equations Différentielles5

3.1 Définition générale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 5

3.2 Equations différentielles du 1er ordre . . . . . . . . . . . . . . .. . . . . . . . . . . . . 6

3.2.1 Equations à variables séparables . . . . . . . . . . . . . . . . .. . . . . . . . . 6

3.2.2 Equation différentielle linéaire à coefficients constants . . . . . . . . . . . . . . 6

3.2.2.1 Equation homogène . . . . . . . . . . . . . . . . . . . . . . . . . . . .6

3.2.3 Equation avec second membre . . . . . . . . . . . . . . . . . . . . . .. . . . . 7

3.2.4 Equations différentielles linéaires à coefficients nonconstants . . . . . . . . . . 9

3.2.5 Equations différentielles homogènes en x et y . . . . . . . .. . . . . . . . . . 12

3.3 Equations différentielles du second ordre . . . . . . . . . . . .. . . . . . . . . . . . . . 13

3.3.1 Equations du 2

ndordre se ramenant au 1erordre . . . . . . . . . . . . . . . . . 13

3.3.1.1 Equations du type : F(x,y",y")=0 . . . . . . . . . . . . . . . .. . . . 13

3.3.1.2 Equations du type : F ( y , y" , y" ) = 0 . . . . . . . . . . . . . . . .14

3.3.1.3 Equations du type : F ( x, y , y" , y" ) = 0 homogène en y,y",y" . . . 15

3.3.2 Equations linéaires homogènes à coefficients constants . . . . . . . . . . . . . 15

3.3.3 Equations linéaires à coefficients constants avec second membre . . . . . . . . 17

3.3.3.1 cas particuliers :f(x)est polynôme de degré n . . . . . . . . . . . . 17

3.3.3.2 cas particuliers :f=Keαx. . . . . . . . . . . . . . . . . . . . . . . . 18

3.3.3.3 cas particuliers :f=eαxP(x). . . . . . . . . . . . . . . . . . . . . 20

3.3.3.4 cas particuliers :f(x) =Ksin(ax)ouf(x) =Kcos(ax). . . . . . . . 22

Maths Rappels

4TABLE DES MATIÈRES

Maths Rappels

Chapitre 3Equations Différentielles

Ce document s"intéresse à la solution des équations différentielles du premier et second ordre. Nous

débuterons en donnant la définition générale d"une équationdifférentielle d"ordren. Puis, nous étudierons

plus particulièrement les solutions des équations du premier ordre, puis celle du second ordre. Pour chaque

cas présenté un exemple illustratif est donné et résolu.

3.1 Définition générale

On appelle équation différentielle d"ordren,nN,une équation de la forme : n k=0a k(x)dky dxk(x) =b(x) avec : yla fonction cherchée b(x)est appelésecond membrede l"équation a k(x)des fonctions dexetan= 0.

Si les fonctionsaksont des constantes, alors on dit que l"équation différentielle est à coefficients

constants.

On rappelle que

d 0y dx0(x) =y

Dans la suite, on notera

y"(x) la dérivée première de y par rapport à x y(2)ou y" la dérivée seconde de y par rapport à x. y(n)la dérivée nièmede y par rapport à x L"équation différentielle sera ditehomogènesi et seulement sib(x) = 0. L"équation différentielle sera ditenormaliséesi et seulement sian(x) = 1.

La résolution de l"équation homogène suppose la détermination densolutions indépendantesy1,y2,...,yn

formant une base du sous-espace vectoriel des solutions. Ainsi, il faudra déterminer autant de solutions

que l"ordre de l"équation, la solution générale étant une combinaison linéaire de ces solutions, soit :

y(x) =n k=0α k(x)yk(x)

La solution des équations peut être explicite, dans ce cas onobtient une relation du typey=g(x)ou

x=h(y)mais elle peut être implicite et conduire à une relation du typeF(x,y) = 0.

Maths Rappels

6Equations Différentielles

3.2 Equations différentielles du 1er ordre

3.2.1 Equations à variables séparables

Une équation différentielle est dite à variables séparables si on peut l"écrire sous la forme :

?(x)dx=ψ(y)dy On intègre alors chacun des côtés en considérant les variables indépendantes : ?(x)dx=

ψ(y)dy+C

où C est une constante réelle.

Exemple 3.1:Résoudre l"équation (E1) :

x+yy= 0(E1) avecy=dy dx(E1) peut s"écrire sous la forme : x+ydy dx= 0 On peut séparer les variables en écrivant l"équation sous laforme : ydy=?xdx puis intégrer : ydy=? xdx soit 1

2y2=?12x2+K

où K est une constante réelle d"où la solution de (E1) : x

2+y2=C

où C est une constante réelle

3.2.2 Equation différentielle linéaire à coefficients constants

On cherche les solutions aux équations du type : a 1dy dx(x) +a0y(x) =b(x) oùa0eta1sont des constantes réelles eta1= 0.

Nous débuterons par l"étude des équations homogènes (i.e. avec un second membre nul). Puis en utilisant

les résultats, nous verrons comment résoudre les équationsavec second membre.

3.2.2.1 Equation homogène

Soit l"équation à résoudre :

a 1dy dx(x) +a0y(x) = 0 oùa0eta1sont des constantes réelles eta1= 0. Supposons quey(x)= 0,xalors, nous pouvons écrire : y (x) y(x)+a0a1= 0y(x)y(x)=?a0a1

Maths Rappels

3.2 Equations différentielles du 1er ordre7

Intégrons par rapport àx. La primitive du membre de gauche est :lny(x)+A, donc nous obtenons : lny(x)=?a0 a1x+B

oùBest une constante réelle qui tient compte des constantes d"intégration des deux membres. Prenons

l"exponentielle de la relation précédente, on obtient : y(x)=ea0 a1x+B

Oreα+β=eαeβ, d"où :

y(x)=eBea0 a1x e Best une constante réelle positive. SoitKcette constante. On a alors : y(x) =Kea0 a1x

L"expressionKreprésente une constante positive ou négative, notonsCcette constante réelle. On a

alors : y(x) =Cea0 a1x

Nous obtenons donc une famille de fonctions. La constanteCpourra être calculée pour répondre à un

cas précis à partir, par exemple,d"une condition particulière du type :y(x1) =D.

Exemple 3.2:Résoudre l"équation (E2) :

y (x) +y(x) = 0(E2)

1. en prenant la conditiony(0) = 1

2. en prenant la conditiony(2) =3

2 Solution :Partons de l"équation différentielle : y (x) +y(x) = 0 en supposant quey(x)= 0,x, nous pouvons diviser cette équation pary(x), soit : y (x) y(x)+ 1 = 0 soit : y(x) y(x)=?1 soit : y(x)=ex+A soit : y(x) =Cex

La constanteCdépend de la condition initiale :

1. poury(0) = 1, on obtientC= 1, soity(x) =ex

2. poury(2) =3

2, on obtientC=32e2, soity(x) =32e2x

3.2.3 Equation avec second membre

L"équation différentielle du premier ordre à coefficients constants avec second membre s"écrit :

a 1dy dx(x) +a0y(x) =b(x) oùa0eta1sont des constantes réelles eta1= 0. La méthode de résolution se décompose en deux points :

Maths Rappels

8Equations Différentielles

1. on résoud l"équation homogène : la solution générale est de la forme :

y(x) =Cea0 a1x, a1= 0,CR

2. On considère que la constanteCdépend dex(d"où le nom de la méthode :méthode de la

varaition de la constante), soit : y(x) =C(x)ea0 a1x

Appliquons cette méthode sur le cas général. Puisque l"équation différentielle fait intervenir la dérivée

première, prenons la dérivée de l"expression précédente : y (x) =C(x)ea0 a1x?a0a1C(x)ea0 a1x En injectant cette expression dans l"équation différentielle à résoudre, nous obtenons : a 1 C (x)ea0 a1x?a0a1C(x)ea0 a1x +a0

C(x)ea0a1x

=b(x) soit : a

1C(x)ea0

a1x=b(x) soit : C (x) =b(x) a1ea 0 a1x

En intégrant, on obtient :

C(x) =b(t)

a1ea 0 a1tdt+D

Si on peut calculer explicitement cette intégrale, on en déduit la forme générale de la solution :

y(x) = b(t) a1ea 0 a1tdt+D e a0a1x La valeur deDest obtenue à partir d"une condition aux limites.

Exemple 3.3:Résoudre l"équation (E3) :

y (x) +y(x) = 1(E3) avec la condition initialey(0) = 2

L"équation homogène associée est :

y (x) +y(x) = 0 Sa solution a été déterminée dans l"exemple précédent, nousavons donc : y(x) =Bex Supposons à present queBdépend de la variablex. On a alors :y(x) =B(x)ex. y (x) =B(x)ex?B(x)ex En injectant ces expressions dans l"équation différentielle, nous obtenons : B (x)ex?B(x)ex+B(x)ex= 1

Soit :

B (x)ex= 1B(x) =ex Une primitive particulière deexpeut s"écrire : e tdt

Maths Rappels

3.2 Equations différentielles du 1er ordre9

Un calcul simple donne :

e tdt=ex d"où

B(x) =ex+C

L"expression générale de la solution de l"équation différentielle est donc : y(x) = [ex+C]ex= 1 +Cex

La constanteCpeut être calculée à partir de la condition initialey(0) = 2. On obtient alors :

y(0) = 1 +Ce0= 1 +C d"oùC= 1. La solution est donc : y(x) = 1 +ex

3.2.4 Equations différentielles linéaires à coefficients non constants

On considère ici les équations du type

A(x)y+B(x)y=f(x)

oùA(x),B(x)etf(x)sont des fonctions de la variable réelle x. La procédure d"intégration est semblable

à celle suivie pour résoudre une équation différentielle linéaire à coefficients constants et se déroule donc

en 2 étapes :

1.intégration sans second membre :A(x)y1+B(x)y1= 0

On résoud l"équation différentielle à variables séparables: dy 1 y1=?B(x)A(x)dx on obtient alors une solution du type y

1=Ceu(x)

oùu(x) =?B(x)dx

A(x)et C est une constante réelle.

2.intégration de l"équation complète : méthode de la variation de la constante

On recherche une solution particulière de l"équation avec second membre de la forme : y

2=C(x)eu(x)

On considère donc maintenant C comme une fonction de x (et nonplus comme une constante) et on cherche à déterminer C(x) telle que : y

2=C(x)eu(x)

soit solution de l"équation différentielle avec le second membre.

3.solution de l"équation complèteSachant que siy1(x)est une solution de l"équation sans 2ndmembre ety2(x)une solution particulière

de l"équation complète alorsy(x) =y1(x) +y2(x)est solution de l"équation complète, la solution

de l"équation avec second membre s"écrit : y=eu(x)(K+C(x)) où K est une constante réelle.

Maths Rappels

10Equations Différentielles

Exemple 3.4:Déterminer l"ensemble des solutions de l"équation différentielle (E4) : y +2x (1 +x2)y= 1(E4)

IciA(x) = 1,B(x) =2x

quotesdbs_dbs33.pdfusesText_39
[PDF] dérivées partielles exercices corrigés

[PDF] dérivée partielle pdf

[PDF] différentielle totale

[PDF] dérivée partielle fonction composée

[PDF] dérivées partielles secondes

[PDF] dérivée totale

[PDF] différentielle totale exemple

[PDF] dérivée racine carrée

[PDF] dérivée u puissance n

[PDF] formule dérivée

[PDF] dérivée seconde exponentielle

[PDF] convexe

[PDF] nombre dérivé 1ere sti2d

[PDF] primitive terminale sti2d

[PDF] tableau dérivée sti2d