[PDF] Chapitre 1 Oscillateur harmonique

Gfkgjogùfjopùjophblkgmù jkhgùf johpù jop

17 juin 2013 On reprend la solution de l'équation différentielle pour le cas d'un système masse-ressort horizontal avec forces de frottements F : Page 13 ...

1 Oscillateur harmonique

8 sept. 2013 ... ressort) on trouve l'équation différentielle de x(t) : ... Par analogie avec le cas du système simple {masse unique + ressort}

Exercice 1 Déterminer léquation de mouvement du système masse

Déterminer l'équation de mouvement du système masse ressort amortisseur suivant : On obtient l'équation de mouvement qui est une équation différentielle de ...

Chapitre 1.6 – Loscillation vertical dun système bloc-ressort

différentielle égale à l'oscillateur harmonique simple. OHS dont Analysons l'énergie d'un système masse-ressort oscillant à la verticale avec les équations du.

Système masse-ressort Une masse fixée à lextrémité libre dun

ressort hélicoïdal constitue un système masse-ressort. Pour de petits allongements ... équation différentielle semblable à celle pour le mouvement harmonique ...

Étude dun oscillateur (système masse-ressort)

18 juin 2012 Mots-clefs du projet : masse-ressort simulation

Partie 1 : Vibrations des systèmes linéaires de second ordre

21 août 2017 canonique de l'équation différentielle régissant le l'évolution du système. ... d'une masselotte de masse m et d'un ressort de raideur k. Par ...

Chapitre 1 Oscillateur harmonique

0 = r k m appelée la pulsation propre du système et dépendant uniquement des grandeurs du système : la raideur du ressort k et la masse m. b Équation du 

Chapitre I Généralités sur les Vibrations et les équations de Lagrange

IV.2.1 Exemple d'un système forcé amorti (système masse-ressort-amortisseur) V.3.2 Equation différentielle d'un système forcé à deux degrés de liberté ...

Étude dun oscillateur (cas du système masse-ressort)

18 juin 2011 Equation différentielle homogène du second ordre du système Masse-Ressort avec frottement. Régime pseudo-périodique. • La courbe théorique ...

Gfkgjogùfjopùjophblkgmù jkhgùf johpù jop

17 juin 2013 On reprend la solution de l'équation différentielle pour le cas d'un système masse-ressort horizontal avec forces de frottements F : Page 13. 13.

1 Oscillateur harmonique

8 sept. 2013 ... système masse-ressort horizontal non amorti la mise en équation du mouvement de la masse et la résolution de l'équation différentielle ...

Chapitre 1

loi de Newton à un système masse-ressort oscillant à l'horizontale sans frottement génère une équation différentielle égale à l'oscillateur harmonique 

Ressorts et equations differentielles.pdf

1 sept. 2011 I. Un ressort et une masse ... Écrire le système d'équations différentielles vérifiée par x1 et x2 . Introduire 0.

Partie 1 : Vibrations des systèmes linéaires de second ordre

problème dans le cadre d'un système “fermé”. 1.2 Équation canonique. Amortisseur b. Ressort

Cours de mécanique - M13-Oscillateurs

retrouver l'équation différentielle de l'oscillateur harmonique On reprend l'exemple des oscillateurs précédents : système masse-ressort horizontal ou.

Exercice 1 Déterminer léquation de mouvement du système masse

Déterminer l'équation de mouvement du système masse ressort amortisseur On obtient l'équation de mouvement qui est une équation différentielle de ...

Chapitre 1.1a – Les oscillations

L'oscillateur harmonique simple OHS est une équation différentielle dont la ? : Fréquence angulaire naturelle d'oscillation du système masse-ressort ...

Étude dun oscillateur (système masse-ressort)

18 juin 2012 système masse-ressort se basant sur le TP et faisant apparaître les conditions initiales et les différentes équations différentielles.

Chapitre 1 Oscillateur harmonique

Le système masse/ressort horizontal 1D et sans frottement est décrit par une équation différentielle linéaire d'ordre 2 à coefficients constants.

Chapitre 14 : Système solide-ressort - Physagreg

Le système serait donc constitué d’un ressort de longueur à vide l 0 qui lorsque qu’on lui accroche une masse m s’étire jusqu’à la longueur l : b Celui que l’on utilise en théorie (1) : Le ressort est horizontal une masse (ponctuelle) est accrochée à son extrémité

Chapitre 16 – L’oscillation vertical d’un système bloc

système masse-ressort oscillant sans frottement à la verticale est définie par l’équation suivante selon la convention x =y =0 : (2) eq 2 2 2 1 E = m? A +e ou ( ) 2 eq 2 2 1 E = k A +e Condition d’équilibre :x =y =0 lorsque e =e eq et mg =keeq où E: Énergie total du système masse-ressort à la verticale (J) k: Constant du

LE SYSTEME MASSE RESSORT - Physagreg

LE SYSTEME MASSE RESSORT La force F exercée par le ressort sur le solide accroché au bout du ressort est appelée force de rappel Elle est proportionnelle à l’allongement x du ressort : F kxi & avec k la constante de raideur du ressort et s’exprime N m1 Détermination de k : On suspend le ressort verticalement

Chapitre 12a – La dynamique du mouvement harmonique simple

loi de Newton à un système masse-ressort oscillant à l’horizontale sans frottement génère une équation différentielle égale à l’oscillateur harmonique simple OHS dont la solution est le mouvement harmonique simple MHS La fréquence naturelle d’oscillation ?

systemes differentiels - Université Paris-Saclay

Ce syst`eme est´equivalent a un syst`eme de 4´equations du premier ordre En e?et on introduit deux nouvelles fonctions inconnues z(t) et w(t) qui repr´esentent les vitesses z(t) = x 0(t) w(t) = y (t) On pose X(t) = x(t) y(t) z(t) w(t) A = 0 0 1 0 0 0 0 1 a1 b1 c1 d1 a2 b2 c2 d2 B(t) = 0 0 b1(t) b2(t)

Comment calculer la compression d’un ressort?

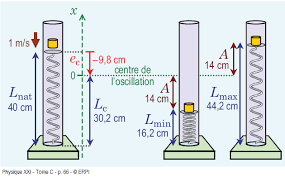
On a appliqué un peu de colle sous le bloc : par conséquent, il demeure collé au ressort et oscille verticalement. On désire déterminer la longueur du ressort (a)au point le plus haut et au point le plus bas de (b) l’oscillation. Évaluons la compression du ressort eqlorsque le bloc est à l’équilibre à l’aide de la 2eièmeloi de Newton selon l’axe .

Comment calculer la longueur d'un ressort?

On laisse tomber un bloc de 0,25 kg dans le tube : au moment où il entre en contact avec le ressort, il se déplace à 1 m/s. On a appliqué un peu de colle sous le bloc : par conséquent, il demeure collé au ressort et oscille verticalement. On désire déterminer la longueur du ressort (a)au point le plus haut et au point le plus bas de (b)

Comment calculer l’Equation différentielle du mouvement ?

Equation différentielle du mouvement : La 2èmeloi de Newton permet d’écrire : P R F ma G avec R &la force de réaction du sol sur le solide accroché au bout du ressort. Or 0 & & & P R (dans la position d’équilibre du ressort) donc F ma G

Comment calculer la force du ressort?

r?mg=0 (Force du ressort et force gravitationnelle) ke?mg=0 (Remplacer la force du ressort, F r=ke) eeq mg k= (Isoler et remplacerk e=e eq, équilibre) Référence : Marc Séguin, Physique XXI Tome C Page 4 Note de cours rédigée par Simon Vézina