Chapter 11 Resource Masters
Lesson 11-5. PDF Pass. Chapter 11. 31. Glencoe Algebra 1. Study Guide and Intervention (continued). Dividing Polynomials. Divide Polynomials by Binomials To
Study Guide And Intervention Dividing Polynomials Answers
Sep 3 2022 Study Guide And Intervention Dividing Polynomials. Answers after that it is not directly done
5-2 - Study Guide and Intervention
11. Glencoe Algebra 2. Study Guide and Intervention. Dividing Polynomials. 5-2. Long Division To divide a polynomial by a monomial use the skills learned
Answers
Lesson 11-5. Chapter 11. 3. 1. Glencoe Algebra 1. Stu d y G u id e an d. In terven tio n. (continued). Dividing Polynomials. Divide Polynomials by Binomials.
Untitled
5-. Study Guide and Intervention (continued). Monomials Use Long Division To divide a polynomial by a monomial use the properties of powers.
Untitled
8-1 Study Guide and Intervention. Multiplying Monomials. Multiply Monomials A monomial is a number a variable
Study Guide and Intervention Workbook
organized by chapter and lesson with two Study Guide and Intervention 5-2 Solving Inequalities by Multiplication ... 11-5 Dividing Polynomials .
5-2 Study Guide and Intervention - Medians and Altitudes of Triangles
11. Glencoe Geometry. 5-2 Study Guide and Intervention. Medians and Altitudes of Triangles. Medians A median is a line segment that connects a vertex of a
Untitled
7-2 Study Guide and Intervention. Division Properties of Exponents. Divide Monomials To divide two powers with the same base subtract the exponents.
Untitled
Chapter 5 Study Guide. 5-1 Study Guide - Operations with Polynomials. Multiply and Divide Monomials Negative exponents are a way of expressing the
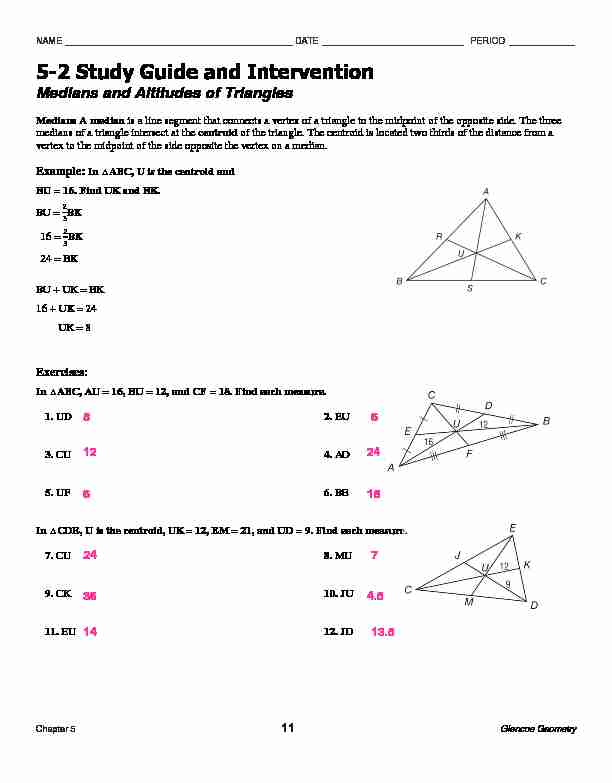
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Chapter 5 11 Glencoe Geometry
5-2 Study Guide and Intervention
Medians and Altitudes of Triangles
Medians A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. The three
medians of a triangle intersect at the centroid of the triangle. The centroid is located two thirds of the distance from a
vertex to the midpoint of the side opposite the vertex on a median.Example: In ᇞABC, U is the centroid and
BU = 16. Find UK and BK.
7BK 7BK24 = BK
BU + UK = BK
16 + UK = 24
UK = 8
Exercises:
In ᇞABC, AU = 16, BU = 12, and CF = 18. Find each measure.1. UD 2. EU
3. CU 4. AD
5. UF 6. BE
In ᇞCDE, U is the centroid, UK = 12, EM = 21, and UD = 9. Find each measure.7. CU 8. MU
9. CK 10. JU
11. EU 12. JD
8 6 12 24 6 18 24 736 4.5
14 13.5
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Chapter 5 12 Glencoe Geometry
5-2 Study Guide and Intervention (continued)
Medians and Altitudes of Triangles
Altitudes An altitude of a triangle is a segment from a vertex to the line containing the opposite side meeting at a right
angle. Every triangle has three altitudes which meet at a point called the orthocenter.Example: The vertices of ᇞABC are A(1, 3),
B(7, 7) and C(9, 3). Find the coordinates of the
orthocenter of ᇞABC. Find the point where two of the three altitudes intersect. has a slope of ଵ 6. y ݕଵ = m(x ݔଵ) Point-slope form y 3 = ଵ6(x 1) m = ଵ
6, (ݔଵ, ݕଵ) = A(1, 3)
y 3 = ଵ6x ଵ
6 Distributive Property
y = ଵ6x + ହ
6 Simplify.
Find the equation of the altitude from
7, then the altitude has a slope
of ଷ 6. y ݕଵ = m(x ݔଵ) Point-slope form y 3 = ଷ6(x 9) m = ଷ
6, (ݔଵ, ݕଵ) = C(9, 3)
y 3 = ଷ6 Distributive Property
y = ଷ6x + ଷଷ
6 Simplify.
Solve the system of equations and find where the altitudes meet. y = ଵ6x + ହ
6 y = ଷ
6x + ଷଷ
6 Original equations
6x + ହ
6 = ଷ
6x + ଷଷ
6 Substitute ଵ
6x + ହ
6 for y.
6 x + ଷଷ
6 Subtract ଵ
6x from each side.
x Subtract ଷଷ6 from each side.
7 = x Divide each side by 2.
y = ଵ6x + ହ
6 = ଵ
6 (7) + ହ
6 =
6 + ହ
6 = 6 The coordinates of the orthocenter of ᇞABC are (7, 6).Exercises:
COORDINATE GEOMETRY Find the coordinates of the orthocenter of the triangle with the given vertices.1. J(1, 0), H(6, 0), I(3, 6) 2. S(1, 0), T(4, 7), U
(3, 1) (1, 0)quotesdbs_dbs31.pdfusesText_37[PDF] 11 7 study guide and intervention trigonometric ratios
[PDF] 11 8 skills practice rational equations answers
[PDF] 11 alive news anchor faith
[PDF] 11 alive news anchor fired
[PDF] 11 alive news anchor vinny
[PDF] 11 alive news trafficking
[PDF] 11 alive news weather radar
[PDF] 11 alive weather alerts
[PDF] 11 alive weather lady
[PDF] 11 alive weather report
[PDF] 11 pro max 64gb green
[PDF] 11 pro max charger box
[PDF] 11 pro max charger cable
[PDF] 11 pro max charger case
