 Answer on Question #43589 Programming
Answer on Question #43589 Programming
https://www.assignmentexpert.com/homework-answers/programming-answer-43589.pdf
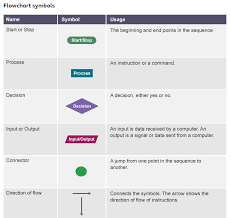 Computer Science - Flowcharts & Binary Year 9
Computer Science - Flowcharts & Binary Year 9
Binary. Binary describes a numbering scheme in which there are only two possible values for each digit: 0 and 1. Flow Charts. A flow chart is a graphical or
 1 Binary systems and hexadecimal
1 Binary systems and hexadecimal
However no matter how complex the system
 Chapter 2 – Number Systems and Codes
Chapter 2 – Number Systems and Codes
This flowchart describes the process and can be used to convert from decimal 2-3 Hexadecimal Number System – Hex to Binary. • Leading zeros can be added ...
 UNIT - 1.1 INTRODUCTION TO COMPUTER
UNIT - 1.1 INTRODUCTION TO COMPUTER
(2) Hexadecimal to Binary Conversion. Convert the 8B2F.9A(16) to its binary Flowchart: Algorithm: Step1 : Start. Step2 : READ a b
 NUMBER SYSTEM CONVERSIONS
NUMBER SYSTEM CONVERSIONS
Therefore through a two-step conversion process
 Express algorithms as flowcharts and written description. Accurately
Express algorithms as flowcharts and written description. Accurately
Convert an algorithm into an accurate flowchart with only minor errors. Create To be able to convert hexadecimal to binary and vice versa. To be able to ...
 Cambridge IGCSE 0478 Computer Science syllabus for examination
Cambridge IGCSE 0478 Computer Science syllabus for examination
• standard flowchart symbols that must be used by students when drawing flowcharts • use different number systems including binary
 PIC16C5X / PIC16CXXX Math Utility Routines
PIC16C5X / PIC16CXXX Math Utility Routines
FIGURE 2: Flowchart for Binary to BCD. Conversion. Spec. Program. Memory Clock Cycles : 81 (worst case when W = 63 Hex ). 00014 ;. ( i.e max Decimal number 99 ).
 Programming with C - Lab
Programming with C - Lab
On flowcharts different geometric shapes are used called flowchart symbols. Some namely binary decimal
 Basic Computer
Basic Computer
flowchart pseudocode
 Worked solutions to selected problems
Worked solutions to selected problems
Convert each digit from hexadecimal to binary: 0011 1111 1101 1010 0001 0000 0100 flowchart for such a routine and a simple assembler code program is.
 Implementation of Number Base Conversions using LabVIEW
Implementation of Number Base Conversions using LabVIEW
The conversion from and to binary octal
 Review Exam 1
Review Exam 1
Hex to Decimal (signed and unsigned). – Binary to Hex. – Hex to Binary. – Addition and subtraction of fixed-length hex numbers.
 Number Input
Number Input
binary and hexadecimal representations are what most computers use; and ASCII A flowchart shows the flow of information input to processed.
 Answer on Question #43589 Programming
Answer on Question #43589 Programming
https://www.assignmentexpert.com/homework-answers/programming-answer-43589.pdf
 CHAPTER 1 Discrete Systems
CHAPTER 1 Discrete Systems
Before beginning with the theory of sets we pause to review the binary and hexadecimal number systems. Although not absolutely fundamental for.
 hexadecimal-to-decimal conversion
hexadecimal-to-decimal conversion
example conversions between number systems decimal binary hex FLOWCHART (representing the subtraction of powers method).
 UNIT - 1.1 INTRODUCTION TO COMPUTER
UNIT - 1.1 INTRODUCTION TO COMPUTER
The block diagram of the computer system have the following three units each functional (3) Binary to Hexadecimal Conversion. Example:.
 ASSEMBLY LANGUAGE TUTORIAL - Simply Easy Learning by
ASSEMBLY LANGUAGE TUTORIAL - Simply Easy Learning by
hexadecimal number system represents a binary data by dividing each byte in half and expressing the value of each half-byte. The following table provides
 [PDF] Basic Computer
[PDF] Basic Computer
algorithm and draw a flowchart to read the grades and find their sum and print it Describe the decimal binary hexadecimal and octal system
 binary to hexadecimal [classic] - Creately
binary to hexadecimal [classic] - Creately
Program from Binary to hexadecimal Excel or any other documents You can export it as a PDF for high-quality printouts flowflowchartbusinessworkflow
 [PDF] NUMBER SYSTEM CONVERSIONS - ipsgwaliororg
[PDF] NUMBER SYSTEM CONVERSIONS - ipsgwaliororg
An equally easy way to convert from binary to hexadecimal is to group binary digits into sets of four starting with the least significant (rightmost) digits
 [PDF] 1 Binary systems and hexadecimal - GCE AL
[PDF] 1 Binary systems and hexadecimal - GCE AL
1 1 Introduction As you progress through this book you will begin to realise how complex computer systems really are By the time you reach Chapter 12 you
 [PDF] Decimal Hexadecimal and Binary Numbers
[PDF] Decimal Hexadecimal and Binary Numbers
Decimal Hexadecimal and Binary Numbers Binary Hex and Decimal Numbers (4-bit representation) Binary Use Flowcharts to Help Plan Program Structure
 [PDF] Computer Science - Flowcharts & Binary Year 9 - Amazon AWS
[PDF] Computer Science - Flowcharts & Binary Year 9 - Amazon AWS
A flow chart is a graphical or symbolic representation of a process Convert the following from binary to hex: 1 00001111 2 00100100
 [PDF] Flow Chart For Converting Binary To Octal
[PDF] Flow Chart For Converting Binary To Octal
25 jan 2023 · Flow Chart for Binary to Decimal Conversion? Computer Science Draw the flowchart for converting the hexadecimal to binary value
 [PDF] Decimal-Binary-Hexadecimal Conversion Chart
[PDF] Decimal-Binary-Hexadecimal Conversion Chart
This chart shows all of the combinations of decimal binary and hexadecimal from 0 to 255 decimal When making a change in a CV this chart will show the
 (PDF) Number List_ Decimal Binary Octal Hexadecimal Ternary
(PDF) Number List_ Decimal Binary Octal Hexadecimal Ternary
4/2/2014 Number list: Decimal binary octal hexadecimal ternary quaternary and dozenal The script is also available as a flow chart pdf
How to convert 1111 binary to hexadecimal?
1110E 1111 F 10000 10 100000 20 What is the first step in converting binary to hexadecimal?
The steps to convert binary to hexadecimal are: Break down the binary number into groups with 4 digits in each group. By looking at the conversion table, write the hexadecimal equivalent of each of the groups. Combine all the numbers together to get the hexadecimal number.How to convert base 10 to base-16?
Converting base-10 to base-16
You divide the number by the exponent (16) and keep dividing the result until the quotient is 0. At each step you multiply the remainder by 16 to get the hex value. The final step is to string together the hex values, starting with the last value.- First convert this into decimal number: = (1101010)2 = 1x26+1x25+0x24+1x23+0x22+1x21+0x20 = 64+32+0+8+0+2+0 = (106)10 Then, convert it into hexadecimal number = (106)10 = 6x161+10x160 = (6A)16 which is answer.
Worked solutions to selected
problemsCHAPI'ER 2
2.1 (a) [1000110101h = 1 x 2
9 + 0 X 2 8 + 0 X 2' + 0 X 26 + 1 X 2
5 + 1X 24 + 0 X 2
3 + 1 X 22 + 0 X 21 + 1 X 20 = 512 + 32 + 16 + 4 + 1 = [565].0 (b) [0.1000110101h = 1 x 2- 1 + 0 X 2- 2 + 0 X 2-3 + 0 X 2- 4 + 1 X 2- 5 + 1 X 2- 6 + 0 X 2-' + 1 X 2- 8 + 0 X 2- 9 + 1 X 2- 10 = 0.5 + 0.03125 + 0.015625 + 3.90625 x 10- 3 + 9.765625 X 10- 4 = [0.5517578125]102.2 To convert a decimal integer into binary the algorithm is to repeatedly
divide it by two.The sequence of remainders written last (the MSB)
to first (the LSB) is the resulting binary number.For a fractional
number the algorithm is to multiply the fraction repeatedly when the sequence of carries over the decimal point form the binary number. (a) Integer (b) Fraction2) 21345 (1 0.673
2) 10672 (0 2
2)5336 (0 1.346 2) 2668 (0 2
2) 1334 (0 0.692
22) 667 (1
1.3842) 333 (1 2
2)166 (0 0.768
2) 83 (1 2
2) 41 (1 1.536
432 I LI ____ W_O_R_K_E_D_S_O_L_U_T_I_O_N_S_T_O_S_E_L_E_CfE __ D_P_R_O_B_L_E_M_S ___ --'
2) 20 (0
2) 10 (0
2) 5 (12) 2 (1
1 (0 = [0101001101100001hBreaking this into groups
of four, starting from the right, gives:0101 0011 0110 0001
or [ 5 3 6 1 h6 2 1.072 2 0.144 2 0.288 2 0.576 = [0.1010110hBreaking into groups of
four, working right from the binary point gives:0.1010 1100
or [0.ACh62.3 [3FDAI04E]16
Convert each digit from hexadecimal
to binary:0011 1111 1101 1010 0001 0000 0100 0111
Now divide into groups of three starting at the right-hand side:00 111 111 110 110 100 001 000 001 000 111
Interpret each group as an octal number giving:
[0 7 7 6 64 1 0 1 0 7]8
2.4 (a) [1220]4; (b) [0.11233k
2.5 +63-125 -0.125 (a) Signed magnitude
00111111
11111101
10010000
tBinary point (b) 2's complement (c) Offset binary
001111:11 10111111
10000011 00000011
11100000 01000000
t tBinary point Binary point
2.6 The received number comprises the data to be checked together with remainder, both of which could have become erroneous during transmission.The check is to divide the complete number by the
constant + x 3 + X + 1):101010) 1010111111100 11000011
101010
111111
101010
101010
101010
00000o
______ W_O_R_K_E_D __ S_O_L_U_T_I_O_N_S_T_O __ S_E_LE_CTE ___ D __ P_R_O_B_L_E_M_S ______ I 433The remainder is zero, indicating that the data
10101111 is correct.
2.7 (a) 11011.1101 x
22 = 0.110111101 X 27
The IEEE P754 single-precision format is a 32-bit grouping interpreted as: ( -IY2"-127(1·f) where s is the sign digit, e is an 8-bit biased exponent and f is a 23-bit unsigned integer.For the above number, e -
127 = 7 and e = 134 = [1000011112
The floating-point representation is then:
o 10000111 110111101()()()()()()()(Table SI Problem 3.2(a).
(i)Location Instruction Mnemonic Comment (Hex) (Hex)
00 28.06 LDM 06 Fetch loop constant to modifier
01 0009 CLR Clear accumulator
58 FFIM STA FFIM Store accumulator in modified address
8003 jMPM 03 Jump if modifier zero to own location,
i.e. stop0008 INCM Add + 1 to modifier
8002JMP
02 Jump to start of loop
06 FF61 Loop constant (2'scomplement of 9F)
(ii)Location Instruction Mnemonic Comment
(Hex) (Hex)00 0009 CLR Clear accumulator
01 58 lOll STA lOll Store accumulator in indirect address
02 5008 LDA 08 Fetch operand address
03 4809 SUB 09 Subtract OOF, i.e. last location cleared
04 98 JMPO 04 Jump to self if accumulator zero, i.e. stop
05 40 OA ADD OA Add 0100, i.e. OOFF + 1 (incrementing
by 1)06 5808 STA 08 Replace modified address
7 8000
JMP00 Jump back to start of loop
08 60 Operand address
09 OOFF Loop constant
OA 0100 Increment constant
434I I
WORKED SOLUTIONS TO SELECTED PROBLEMS
Table S2 Problem 3.2(b).
(i)Location Instruction MnemOnic Comment
(Hex) (Hex)00 2808 LDM 08 Fetch loop constant to modifier
01 0009 CLR Clear accumulator
40 07 ADD 07 Add + 1 to accumulator
58 FFIM STA FFIM Store accumulator in modified address
AOO4 )MPM 04 Jump to self if zero, i.e. stop
0008 INCM Add + 1 to modifier
8002JMP
02 Jump back to start of loop
07 1 Constant +1
08 FF61 Loop constant (2's complement of 9F)
(ii)Location Instruction Mnemonic Comment
(Hex) (Hex)00 SOOA LDA OA Fetch count to accumulator
01 400B ADD OB Add +1
02 580A STA OA Replace in memory
03 58 OCII STA OCII Store count in indirect address
04 SOOC LDA OC Fetch operand address
05 48 OD SUB OD Test for end" of loop
06 9806 JMP006 Jump to self if zero
07 40 OE ADD OE Increment operand address by + 1
08 580C STA OC Replace in memory
8000JMP
00 Jump back to start of loop
OA ( ) Accumulating number
OB 1 Constant +1
OC 60 Operand address
OD OOFF Loop constant
OE 0100 Increment constant
(b) 1.01110101 X 2- 12 = 0.101110101 X 2- 11 and e -127 = 11 giving e = 138 and the as: o 10001011 10111010100000000000000 (c) -0.110101011 x 2 6 gives1 10000110 11010101100000000000000
(d) -0.000001101 x 2- 1 gives1 01111001
1101000000000000000
WORKED SOLUTIONS TO SELECfED PROBLEMS
TableS3 Problem 3.3.
Location
Instruction Mnemonic Comment
(Hex) (Hex)28 10 LDY 10
8OAOIDA _}
9806 )MPO 06
A003 ]MPM 03 Test for zero loop
0008 JNCM
80 01 JMP 01
06 0005 EXAM
07 8011 STA 11
08 0005 EXAM
09 8011 LDA 11
OA 40 12 ADD 12 Unpacking of address of zero locationOB 58 1311 STA 1311 and storing in table
OC 80 13 LDA 13
OD 40 14 ADD 14
OE 58 13 STA 13
F 8003
JMP 03 10FFa) Test loop constant, -0040
11 ( ) Temporary store
12 AO13 Al Address table constants
14 1CHAPl'ER 3
3.2 Machine-code programs for this problem are given in Tables Sl and
S2.3.3 A typical program for this problem is shown in Table S3. Note that
in this program we are by having only one modifier register and not being able to increment a memory location directly. The 'test for zero' loop employs the modifier register to increase the speed of operation of the program and the 'unpacking' of the address is performed using indirect addressing. An alternative approach is to use the indirect address function for the test loop, since the actual address could then be held in the indirectly addressed location.3.4 In this program, given in Table S4, we can take advantage
of the fact that the same modifier constant can be used; therefore we can employ a modified instruction for both transfers.3.7 This program is shown in Table
S5. The basic logic is to extract the 4-
bit BCD digits using the AND function and then to multiply by I I 435436 I 1L-___ W_O_R_KE __ D_S_O_L_UT_I_O_N_S_T_O_S_E_L_E_cr_E_D_P_R_O_B_L_E_M_S ___ ---I
Table S4 Problem 3.4.
Location
Instruction Mnemonic Comment (Hex) (Hex)
00 28 OA
01 SO 801M
02 58 OA
03 SO FOIM
04 58 801M
05 SOOA
06 58 FOIM
07 AO 07
08 0008
80 01OA FFEO
OB ( )
Table SS Problem 3.7.
Location Instruction (Hex) (Hex)
00 28 OE
01 SO OF
02 9806
03 SO OF
04 13 04
05 58 OF
06 6011
07 40 10
08 A008
09 0008
OA AS 12
quotesdbs_dbs14.pdfusesText_20[PDF] flower dictionary with pictures book
[PDF] flower emoji meanings
[PDF] flower encyclopedia pdf
[PDF] flower meaning gratitude
[PDF] flower names and meanings
[PDF] flower names and pictures pdf
[PDF] flowers and their meanings in literature
[PDF] flowers name pdf download
[PDF] flowers of bengal
[PDF] flowers pdf download
[PDF] flu cases world map
[PDF] flu deaths 2018 2019
[PDF] flu deaths 2019
[PDF] flu deaths 2019 usa by age group
