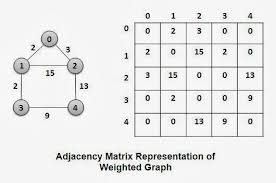
 UNIT 5 - GRAPHS The Graph ADT Introduction Definition Graph
UNIT 5 - GRAPHS The Graph ADT Introduction Definition Graph
Euler used graph theory to solve Seven Bridges of Königsberg problem. Is A circuit having three vertices and three edges. Page 5. 5. Sub Graph. A graph S is ...
 Graph Theory - Lecture notes.
Graph Theory - Lecture notes.
28-Apr-2019 • These are written for the introductory course on graph theory to ... pdf. Page 34. 28. Spanning Trees. Page 35. Chapter 5. Extremal Graph Theory.
 Graph Theory lecture notes
Graph Theory lecture notes
Definition 1.3. The degree of a vertex v written d(v)
 Lecture 17: Introduction to Graph Theory 1 Preliminaries
Lecture 17: Introduction to Graph Theory 1 Preliminaries
14-Oct-2019 written deg(v) is the number of non-self-loop edges adjacent to v ... Graph Theory Notes [PDF]. Available:https://homepages.warwick.ac.uk ...
 An Introduction to Algebraic Graph Theory
An Introduction to Algebraic Graph Theory
25-Mar-2021 Sug- gestions and comments on how to improve the notes are also welcomed. ... For any graph G the chromatic polynomial PG(k) can be written in ...
 Lecture Notes on Discrete Mathematics
Lecture Notes on Discrete Mathematics
30-Jul-2019 This paradox amongst others opened the stage for the development of axiomatic set theory. ... graph G − e = (V
 Lecture Notes on Graph Theory
Lecture Notes on Graph Theory
30-Nov-2017 This book is written for the students of Computer Science who study the subject Graph. Theory under their university curriculum. The content of ...
 Graph-based segmentation of letters in handwriting words with
Graph-based segmentation of letters in handwriting words with
Our major contribution is to combine template matching techniques with graph theory to identify the letters on the processed image. Specifically we first
 Discrete Structures Lecture Notes
Discrete Structures Lecture Notes
written as 2 > 1. How convenient! Common mathematical relations that will concern ... For graph theory initiates such questions present no difficulty separating.
 Graph Theory lecture notes
Graph Theory lecture notes
The complement of G written G or Ge
 Graph-based segmentation of letters in handwriting words with
Graph-based segmentation of letters in handwriting words with
contribution is to combine template matching techniques with graph theory to the handwritten letters with warped templates and optimizes the spatial ...
 PDF Graph Theory - Tutorialspoint
PDF Graph Theory - Tutorialspoint
This tutorial offers a brief introduction to the fundamentals of graph theory. Written in a reader-friendly style it covers the types of graphs
 ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
Network topology-Definitions Graph
 Graph Theory
Graph Theory
18-Aug-2016 Much of the material in these notes is from the books Graph Theory by ... The line graph of G written L(G)
 Lecture Notes on Discrete Mathematics
Lecture Notes on Discrete Mathematics
30-Jul-2019 This chapter will be devoted to understanding set theory ... Corresponding to a
 Handwritten signature identification using basic concepts of graph
Handwritten signature identification using basic concepts of graph
Key-Words: - handwritten signature signature recognition
 Discrete Structures Lecture Notes
Discrete Structures Lecture Notes
15.2 Graph coloring . ments using the fertile ground of number theory. ... A composite number n can be written as a product n = ab of two strictly ...
 An Introduction to Combinatorics and Graph Theory
An Introduction to Combinatorics and Graph Theory
Graph theory is concerned with various types of networks the pattern when all previous letters have been used to the left of the new one. For example
 Graph Theory with Applications to Engineering and Computer
Graph Theory with Applications to Engineering and Computer
applications and is written for an advanced student of graph theory. constructing variable-length binary codes where the letters of the alphabet (A
 Graph Theory Handwritten Notes - Gate Vidyalay
Graph Theory Handwritten Notes - Gate Vidyalay
A graph is a collection of vertices connected to each other through a set of edges The study of graphs is known as Graph Theory
 Graph Theory Handwritten Notes Exams Discrete Structures and
Graph Theory Handwritten Notes Exams Discrete Structures and
Partial preview of the text Download Graph Theory Handwritten Notes and more Discrete Structures and Graph Theory Exams in PDF only on Docsity! L plowing back
 [PDF] Graph Theory lecture notes
[PDF] Graph Theory lecture notes
Graph Theory lecture notes 1 Definitions and examples 1–1 Definitions Definition 1 1 A graph is a set of points called vertices together with a
 [PDF] Graph Theory: Penn State Math 485 Lecture Notes
[PDF] Graph Theory: Penn State Math 485 Lecture Notes
This is version two of set of lecture notes for Math 485–Penn State's undergraduate Graph Theory course Since I use these notes while I teach
 GATE Handwritten Notes For CSE Discrete Mathematics Book
GATE Handwritten Notes For CSE Discrete Mathematics Book
Discrete Mathematics Book - II Chapter 4 Graph Theory Notes In PDF Format GATE CSE handwritten Notes that will definitely help you in your CSE Exam
 SOLUTION: Handwritten Notes on Graph Theory - Studypool
SOLUTION: Handwritten Notes on Graph Theory - Studypool
Get help with homework questions from verified tutors 24/7 on demand Access 20 million homework answers class notes and study guides in our Notebank
 (PDF) Lecture Notes on Graph Theory - Academiaedu
(PDF) Lecture Notes on Graph Theory - Academiaedu
Textbook on Graph Theory for Students of Faculty of Mathematics and Informatics at Plovdiv University in Bulgarian
 Graph Theory Handwritten Notes - Gate Vidyalay
Graph Theory Handwritten Notes - Gate Vidyalay
A graph is a collection of vertices connected to each other through a set of edges The study of graphs is known as Graph Theory
 Graph Theory Handwritten Notes Exams Discrete Structures and
Graph Theory Handwritten Notes Exams Discrete Structures and
Partial preview of the text Download Graph Theory Handwritten Notes and more Discrete Structures and Graph Theory Exams in PDF only on Docsity! L plowing back
 [PDF] Graph Theory lecture notes
[PDF] Graph Theory lecture notes
Graph Theory lecture notes 1 Definitions and examples 1–1 Definitions Definition 1 1 A graph is a set of points called vertices together with a
 [PDF] Graph Theory: Penn State Math 485 Lecture Notes
[PDF] Graph Theory: Penn State Math 485 Lecture Notes
This is version two of set of lecture notes for Math 485–Penn State's undergraduate Graph Theory course Since I use these notes while I teach
 Discrete Mathematics Handwritten Notes pdf download bca 2022
Discrete Mathematics Handwritten Notes pdf download bca 2022
Graph Theory: basic terminology models and types multi-graphs and weighted graphs graph representation graph isomorphism connectivity Euler and
 GATE Handwritten Notes For CSE Discrete Mathematics Book
GATE Handwritten Notes For CSE Discrete Mathematics Book
Download free GATE CSE Handwritten Discrete Mathematics Book - II Chapter 4 Graph Theory Notes In PDF Format GATE CSE handwritten Notes that will
 SOLUTION: Handwritten Notes on Graph Theory - Studypool
SOLUTION: Handwritten Notes on Graph Theory - Studypool
Get help with homework questions from verified tutors 24/7 on demand Access 20 million homework answers class notes and study guides in our Notebank
An Introduction to
Combinatorics and Graph
Theory
David Guichard
This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this license, visit or send a letter toCreative Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA. If you distribute
this work or a derivative, include the history of the document. This copy of the text was compiled from source at 11:36 on 3/4/2023. We will be glad to receive corrections and suggestions for improvement atguichard@whitman.edu.Contents
1Fundamentals
71.1Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81.2Combinations and permutations . . . . . . . . . . . . . . . . .
111.3Binomial coefficients . . . . . . . . . . . . . . . . . . . . . . .
161.4Bell numbers . . . . . . . . . . . . . . . . . . . . . . . . . . .
211.5Choice with repetition . . . . . . . . . . . . . . . . . . . . . .
271.6The Pigeonhole Principle . . . . . . . . . . . . . . . . . . . . .
311.7Sperner's Theorem . . . . . . . . . . . . . . . . . . . . . . . .
351.8Stirling numbers . . . . . . . . . . . . . . . . . . . . . . . . .
392
Inclusion-Exclusion
452.1The Inclusion-Exclusion Formula . . . . . . . . . . . . . . . . .
452.2Forbidden Position Permutations . . . . . . . . . . . . . . . . .
483
4Contents
3Generating Functions
533.1Newton's Binomial Theorem . . . . . . . . . . . . . . . . . . .
533.2Exponential Generating Functions . . . . . . . . . . . . . . . .
563.3Partitions of Integers . . . . . . . . . . . . . . . . . . . . . . .
593.4Recurrence Relations . . . . . . . . . . . . . . . . . . . . . . .
623.5Catalan Numbers . . . . . . . . . . . . . . . . . . . . . . . . .
664
Systems of Distinct Representatives
714.1Existence of SDRs . . . . . . . . . . . . . . . . . . . . . . . .
724.2Partial SDRs . . . . . . . . . . . . . . . . . . . . . . . . . . .
744.3Latin Squares . . . . . . . . . . . . . . . . . . . . . . . . . . .
764.4Introduction to Graph Theory . . . . . . . . . . . . . . . . . .
834.5Matchings . . . . . . . . . . . . . . . . . . . . . . . . . . . .
845
Graph Theory
915.1The Basics . . . . . . . . . . . . . . . . . . . . . . . . . . . .
915.2Euler Circuits and Walks . . . . . . . . . . . . . . . . . . . . .
965.3Hamilton Cycles and Paths . . . . . . . . . . . . . . . . . . .
1005.4Bipartite Graphs . . . . . . . . . . . . . . . . . . . . . . . .
1035.5Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1055.6Optimal Spanning Trees . . . . . . . . . . . . . . . . . . . .
1085.7Connectivity . . . . . . . . . . . . . . . . . . . . . . . . . .
1105.8Graph Coloring . . . . . . . . . . . . . . . . . . . . . . . . .
1185.9The Chromatic Polynomial . . . . . . . . . . . . . . . . . . .
1245.10Coloring Planar Graphs . . . . . . . . . . . . . . . . . . . . .
1255.11Directed Graphs . . . . . . . . . . . . . . . . . . . . . . . .
129Contents5
6Polya{Redeld Counting
1356.1Groups of Symmetries . . . . . . . . . . . . . . . . . . . . .
1376.2Burnside's Theorem . . . . . . . . . . . . . . . . . . . . . .
1406.3Polya-Redeld Counting . . . . . . . . . . . . . . . . . . . .
146A Hints 151
Index 153
1
Fundamentals
Combinatorics is often described brie
y as being about counting, and indeed counting is a large part of combinatorics. As the name suggests, however, it is broader than this: it is about combining things. Questions that arise include counting problems: \How many ways can these elements be combined?" But there are other questions, such as whether a certain combination is possible, or what combination is the \best" in some sense. We will see all of these, though counting plays a particularly large role. Graph theory is concerned with various types of networks, or really models of networks called graphs. These are not the graphs of analytic geometry, but what are often described as \points connected by lines", for example: The preferred terminology isvertexfor a point andedgefor a line. The lines need not be straight lines, and in fact the actual denition of a graph is not a geometric denition. The gure above is simply a visualization of a graph; the graph is a more abstract object, consisting of seven vertices, which we might namefv1;:::;v7g, and the collection of pairs of vertices that are connected; for a suitable assignment of namesvito the points in the diagram, the edges could be represented asfv1;v2g,fv2;v3g,fv3;v4g,fv3;v5g,fv4;v5g, fv5;v6g,fv6;v7g. 7 Suppose we have a chess board, and a collection of tiles, like dominoes, each of which is the size of two squares on the chess board. Can the chess board be covered by the dominoes? First we need to be clear on the rules: the board is covered if the dominoes are laid down so that each covers exactly two squares of the board; no dominoes overlap; and every square is covered. The answer is easy: simply by laying out 32 dominoes in rows, the board can be covered. To make the problem more interesting, we allow the board to be rectangular of any size, and we allow some squares to be removed from the board. What can be say about whether the remaining board can be covered? This is such a board, for example: What can we say? Here is an easy observation: each domino must cover two squares, so the total number of squares must be even; the board above has an even number of squares. Is that enough? It is not too hard to convince yourself that this board cannot be covered; is there some general principle at work? Suppose we redraw the board to emphasize that it really is part of a chess board: Aha! Every tile must cover one white and one gray square, but there are four of the former and six of the latter, so it is impossible. Now do we have the whole picture? No;1.1 Examples9
for example: The gray square at the upper right clearly cannot be covered. Unfortunately it is not easy to state a condition that fully characterizes the boards that can be covered; we will see this problem again. Let us note, however, that this problem can also be represented as a graph problem. We introduce a vertex corresponding to each square, and connect two vertices by an edge if their associated squares can be covered by a single domino; here is the previous board: Here the top row of vertices represents the gray squares, the bottom row the white squares. A domino now corresponds to an edge; a covering by dominoes corresponds to a collection of edges that share no endpoints and that areincidentwith (that is, touch) all six vertices. Since no edge is incident with the top left vertex, there is no cover. Perhaps the most famous problem in graph theory concerns map coloring: Given a map of some countries, how many colors are required to color the map so that countries sharing a border get different colors? It was long conjectured that any map could be colored with four colors, and this was nally proved in 1976. Here is an example of a small map, colored with four colors: Typically this problem is turned into a graph theory problem. Suppose we add to each country a capital, and connect capitals across common boundaries. Coloring the capitals so10Chapter 1 Fundamentals
that no two connected capitals share a color is clearly the same problem. For the previous map: Any graph produced in this way will have an important property: it can be drawn so that no edges cross each other; this is aplanargraph. Non-planar graphs can require more than four colors, for example this graph: This is called thecomplete graphon ve vertices, denotedK5; in a complete graph, each vertex is connected to each of the others. Here only the \fat" dots represent vertices; intersections of edges at other points are not vertices. A few minutes spent trying should convince you that this graph cannot be drawn so that its edges don't cross, though the number of edge crossings can be reduced.Exercises 1.1.
1.Explain why anmnboard can be covered if eithermornis even. Explain why it cannot
be covered if bothmandnare odd.2.Suppose two diagonally opposite corners of an ordinary 88 board are removed. Can the
resulting board be covered?3.Suppose thatmandnare both odd. On anmnboard, colored as usual, all four corners
will be the same color, say white. Suppose one white square is removed from any location on the board. Show that the resulting board can be covered.4.Suppose that one corner of an 88 board is removed. Can the remainder be covered by
13 tiles? Show a tiling or prove that it cannot be done.
1.2 Combinations and permutations11
5.Suppose the square in row 3, column 3 of an 88 board is removed. Can the remainder be
covered by 13 tiles? Show a tiling or prove that it cannot be done.6.Remove two diagonally opposite corners of anmnboard, wheremis odd andnis even.
Show that the remainder can be covered with dominoes.7.Suppose one white and one black square are removed from annnboard,neven. Show
that the remainder can be covered by dominoes.8.Suppose annnboard,neven, is covered with dominoes. Show that the number of horizontal
dominoes with a white square under the left end is equal to the number of horizontal dominoes with a black square under the left end.9.In the complete graph on ve vertices shown above, there are ve pairs of edges that cross.
Draw this graph so that only one pair of edges cross. Remember that \edges" do not have to be straight lines.10.Thecomplete bipartite graphK3;3consists of two groups of three vertices each, with all
possible edges between the groups and no other edges:Draw this graph with only one crossing.
We turn rst tocounting. While this sounds simple, perhaps too simple to study, it is not. When we speak of counting, it is shorthand for determining the size of a set, or more often, the sizes of many sets, all with something in common, but different sizes depending on one or more parameters. For example: how many outcomes are possible when a die is rolled? Two dice?ndice? As stated, this is ambiguous: what do we mean by \outcome"? Suppose we roll two dice, say a red die and a green die. Is \red two, green three" a different outcome than \red three, green two"? If yes, we are counting the number of possible \physical" outcomes, namely 36. If no, there are 21. We might even be interested simply in the possible totals, in which case there are 11 outcomes. Even the quite simple rst interpretation relies on some degree of knowledge about counting; we rst make two simple facts explicit. In terms of set sizes, suppose we know that setAhas sizemand setBhas sizen. What is the size ofAandBtogether, that is, the size ofA[B? If we know thatAandBhave no elements in common, then the size A[Bism+n; if they do have elements in common, we need more information. A simple but typical problem of this type: if we roll two dice, how many ways are there to get either7 or 11? Since there are 6 ways to get 7 and two ways to get 11, the answer is 6 + 2 = 8.
quotesdbs_dbs14.pdfusesText_20[PDF] graph theory questions and answers pdf
[PDF] graph theory theorems and proofs pdf
[PDF] graph theory with applications bondy murty solutions
[PDF] graph theory with applications bondy murty solutions pdf
[PDF] graph with 5 vertices of degrees 1
[PDF] graphème definition française
[PDF] graphic design courses in mumbai
[PDF] graphic design curriculum pdf
[PDF] graphic design for visually impaired
[PDF] graphic design manual principles and practice pdf
[PDF] graphic design notes
[PDF] graphic design pdf
[PDF] graphic design portfolio pdf 2019
[PDF] graphic design project pdf

